针对“数据4.1”,讲解回归问题的K近邻算法,以V1(营业利润水平)为响应变量,以V2(固定资产投资)、V3(平均职工人数)、V4(研究开发支出)为特征变量。
1 变量设置及数据处理
data=pd.read_csv(r'数据4.1.csv')X = data.drop(['V1'],axis=1)#设置特征变量,即除V1之外的全部变量y = data['V1']#设置响应变量,即V1X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3, random_state=123)scaler = StandardScaler()scaler.fit(X_train)X_train_s = scaler.transform(X_train)X_test_s = scaler.transform(X_test)
2 构建K近邻回归算法模型
#K近邻算法(K=1)model = KNeighborsRegressor(n_neighbors=1)model.fit(X_train_s, y_train)pred = model.predict(X_test_s)print("K=1时的预测值:{}".format(pred))mean_squared_error(y_test, pred)model.score(X_test_s, y_test)#K近邻算法(K=17)model = KNeighborsRegressor(n_neighbors=17)model.fit(X_train_s, y_train)pred = model.predict(X_test_s)print("K=17时的预测值:{}".format(pred))mean_squared_error(y_test, pred)model.score(X_test_s, y_test)#K近邻算法(K=9)model = KNeighborsRegressor(n_neighbors=9)model.fit(X_train_s, y_train)pred = model.predict(X_test_s)print("K=9时的预测值:{}".format(pred))mean_squared_error(y_test, pred)model.score(X_test_s, y_test)
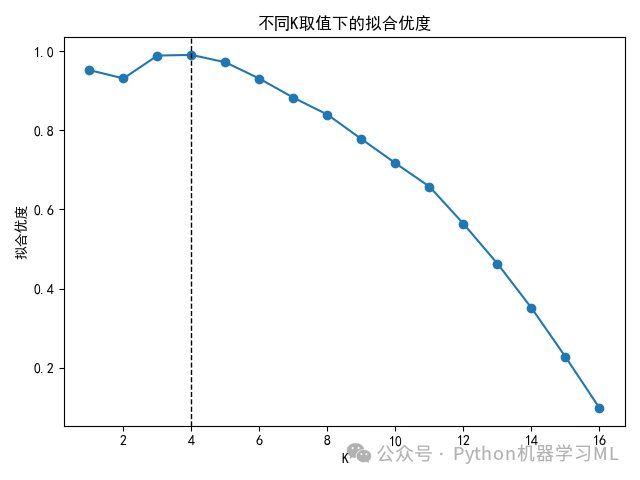
3 如何选择最优的K值
scores = []ks = range(1, 17)for k in ks:model = KNeighborsRegressor(n_neighbors=k)model.fit(X_train_s, y_train)score = model.score(X_test_s, y_test)scores.append(score)print(max(scores))index_max = np.argmax(scores)print(f'最优K值: {ks[index_max]}')#K近邻算法(选取最优K的图形展示)plt.rcParams['font.sans-serif'] = ['SimHei']#本代码的含义是解决图表中中文显示问题。plt.plot(ks, scores, 'o-')plt.xlabel('K')plt.axvline(ks[index_max], linewidth=1, linestyle='--', color='k')plt.ylabel('拟合优度')plt.title('不同K取值下的拟合优度')plt.tight_layout()plt.show()plt.savefig('不同K取值下的拟合优度.png')
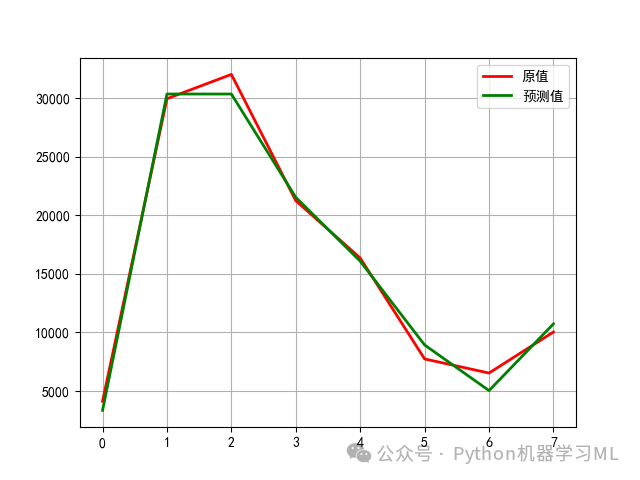
4 最优模型拟合效果图形展示
model = KNeighborsRegressor(n_neighbors=4)model.fit(X_train_s, y_train)pred = model.predict(X_test_s)mean_squared_error(y_test, pred)model.score(X_test_s, y_test)t = np.arange(len(y_test))plt.rcParams['font.sans-serif'] = ['SimHei']#本代码的含义是解决图表中中文显示问题。plt.plot(t, y_test, 'r-', linewidth=2, label=u'原值')plt.plot(t, pred, 'g-', linewidth=2, label=u'预测值')plt.legend(loc='upper right')plt.grid()plt.show()plt.savefig('最优模型拟合效果图形展示.png')