一、盛最多水的容器
11. 盛最多水的容器 - 力扣(LeetCode)
给定一个长度为
n的整数数组height。有n条垂线,第i条线的两个端点是(i, 0)和(i, height[i])。找出其中的两条线,使得它们与
x轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
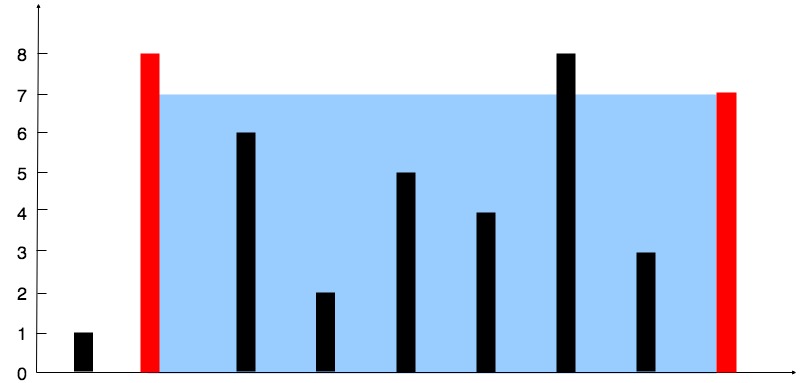
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。示例 2:
输入:height = [1,1] 输出:1提示:
n == height.length2 <= n <=0 <= height[i] <=
解法思路一:暴力枚举法。让第一个垂线分别与其它垂线组合,然后让第二个垂线分别与其它垂线组合,....最终返回最大容量。
代码实现(C++,时间复杂度为O(N^2)):
//方法一:暴力枚举法
class Solution {
public:
int maxArea(vector<int>& height) {
int n = height.size();
int ret = 0; //记录最大容积
//两层for循环,暴力遍历所有情况
for(int i = 0;i < n;i++)
{
for(int j = i + 1;j < n;j++)
{
int V = min(height[i],height[j])*(j - i); //记录当前容器的容量(长*宽)
ret = max(ret,V); //更新ret,使ret保持最大
}
}
return ret;
}
};这种代码适用于数据量少的情景,如果数据非常多,那么就会超时。
在leetcode提交结果如下:

所以我们需要其它思路来解决问题。
暴力求解法之所以不行是因为循环次数太多了(组合情况太多了),每一种情况都需要求容积,然后比较,拿到最大容积。
那我们可不可以减少循环次数来解决问题呢?
我们先用示例1中的数据进行分析:

这就是思路二:对撞指针法。用left和right(两个"指针")来进行控制流程。
代码实现(C++,时间复杂的为O(N)):
//方法二:对撞指针法
class Solution {
public:
int maxArea(vector<int>& height) {
//用left和right来控制区间,ret记录最大容积
int left = 0,right = height.size() - 1,ret = 0;
while(left < right)
{
//记录一个数与另一个数的组合的最大容积
int V = min(height[left],height[right])*(right-left);
//更新ret,使其保持最大容积
ret = max(ret,V);
//哪边小,哪边改变
if(height[left]<height[right]) ++left;
else --right;
}
return ret; //返回最大容积
}
};二、有效三角形个数
611. 有效三角形的个数 - 力扣(LeetCode)
给定一个包含非负整数的数组
nums,返回其中可以组成三角形三条边的三元组个数。示例 1:
输入: nums = [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3示例 2:
输入: nums = [4,2,3,4] 输出: 4提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
看到这题,首先想到可以用暴力枚举求解。从nums中取3个数,将所有情况逐一进行比较。
判断3个数是否为三角形,如果这3个数是无序的,那么我们就需要判断三次(a+b>c,a+c>b,b+c>a),我们可以优化一下,将这3个数先排升序,假设顺序为a,b,c,那么只需判断一次(a+b>c)即可。
代码实现(C++,时间复杂度为O(N^3)):
//方法一:暴力求解法
class Solution {
public:
int triangleNumber(vector<int>& nums) {
// 1. 先排升序
sort(nums.begin(), nums.end());
int n = nums.size(), ret = 0; //ret来计算三元组的个数
// 2. 从小到大枚举所有的三元组
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
for (int k = j + 1; k < n; k++) {
// 当最小的两个边之和大于第三边的时候,统计答案
if (nums[i] + nums[j] > nums[k]) //只需这一个判断条件是因为有序
ret++;
}
}
}
return ret;
}
};这道题用暴力求解是可以做出来的。
但是,暴力求解必定会效率低下,我们还可以用另外一种方法来处理问题。
我们解这道题的首要做法是先将数组中的数据排升序,数组一旦有序,那么我们的操作空间就会变大,对于这道题,解法二就是利用数组的单调性,使用双指针算法来解决问题。具体过程如下:

代码实现(C++,时间复杂度O(N^2)):
//方法二:对撞指针法
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(),nums.end()); //先对数组排升序
int n = nums.size(); //记录数组元素个数
int ret = 0; //记录三元组个数
for(int i = n-1;i>=2;i--) //最外层循环用下标固定c
{
int left = 0,right = i-1; //双"指针",本质都是下标
while(left < right)
{
//a+b>c
if(nums[left]+nums[right] > nums[i])
{
ret += (right-left); //有right-left个三元组
--right; //此时right位置上的数据就没用了,更新right
}
//a+b<=c
else
{
++left; //此时left位置上的数据就没用了,更新left
}
}
}
return ret; //返回全部三元组个数
}
};三、查找总价格为目标值的两个商品
LCR 179. 查找总价格为目标值的两个商品 - 力扣(LeetCode)
购物车内的商品价格按照升序记录于数组
price。请在购物车中找到两个商品的价格总和刚好是target。若存在多种情况,返回任一结果即可。示例 1:
输入:price = [3, 9, 12, 15], target = 18 输出:[3,15] 或者 [15,3]示例 2:
输入:price = [8, 21, 27, 34, 52, 66], target = 61 输出:[27,34] 或者 [34,27]提示:
1 <= price.length <= 10^51 <= price[i] <= 10^61 <= target <= 2*10^6
方法一:暴力枚举法。将数组中所有两两组合的情况全部列举出来相加看是否为target,两层循环即可搞定。
代码实现(C++,时间复杂度O(N^2)):
//方法一:暴力求解法
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
for(int i=0;i<price.size();i++)
{
for(int j=i+1;j<price.size();j++)
{
if(price[i] + price[j] == target)
{
return {price[i],price[j]};
}
}
}
return {-1,-1}; //不存在的情况
}
};这道题用暴力枚举法会超时:

方法二: 利用数组单调性,使用双指针算法解决问题。以示例2为例,具体过程如下:

代码实现(C++,时间复杂度为O(N^2)):
//方法二:对撞指针法
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
int left = 0,right = price.size()-1; //双"指针"
while(left < right) //终止条件是left==right
{
//情况一
if(price[left] + price[right] > target)
--right;
//情况二
else if(price[left] + price[right] < target)
++left;
//情况三
else
return {price[left],price[right]};
}
return {-1,-1}; //不存在的情况
}
};四、三数之和
15. 三数之和 - 力扣(LeetCode)
给你一个整数数组
nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且j != k,同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为0且不重复的三元组。注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。示例 2:
输入:nums = [0,1,1] 输出:[] 解释:唯一可能的三元组和不为 0 。示例 3:
输入:nums = [0,0,0] 输出:[[0,0,0]] 解释:唯一可能的三元组和为 0 。提示:
3 <= nums.length <= 3000-10^5 <= nums[i] <= 10^5
先解释一下三元组"不重复","不重复"是指两个三元组中的数字不完全相同,比如[1,2,3]和[2,3,1]这两个三元组就是重复的,因为它们两个中的数字完全相同(与顺序无关)。返回三元组时,如果要返回[1,2,3],那么返回[2,3,1]也没问题,如果返回多个三元组,那么这些三元组的返回顺序也是任意的,因为返回时与顺序无关。三元组中的数可以重复,但是重复数的下标必须不同。
对于这道题解法一:暴力枚举法,将所有的三元组全部枚举出来依次判断。但这会面临一个问题,如果有两个三元组分别是[1,2,3]和[2,3,1],它们其实是一样的,所以我们需要"去重",去重首先会想到set容器,但是在set容器中[1,2,3]和[2,3,1]是不一样的,所以要想解决这个问题,可以事先对数组进行排序,这样从左往右暴力枚举出来的结果都是有序的三元组,比如[2,3,1]经过排序后变为[1,2,3],这样两个[1,2,3]放进set容器中就可以完成去重。
代码实现(C++,时间复杂度为O(N^3)):
//方法一:暴力枚举法
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(),nums.end()); //排升序
int n = nums.size();
set<vector<int>> s; //用来存放三元组
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
for(int k = j+1;k<n;k++)
{
if(nums[i]+nums[j]+nums[k] == 0)
s.insert({nums[i],nums[j],nums[k]});
}
}
}
vector<vector<int>> vv(s.begin(),s.end());//用于做返回值
return vv;
}
};这道题用暴力枚举法也是会超时的:

为什么要讲一下暴力枚举法呢?
为的是可以使我们可以通过暴力枚举法的思路来在此基础上做出优化。
方法二: 排序+双指针。这道题其实和第三道题差不多,第三道题是求两个数的和是否为一个目标值,而这道题可以转换为两个数的和是否为另外一个数的相反数(因为它们三数相加为0)。另外,这道题还需额外注意两点:1、去重问题 2、不漏数据
举例说明:

这里还有一个小优化的地方:如果固定的数为正数,因为是要排升序,所以正数后面不可能找到两个数相加等于负数,所以如果固定的数是正数,那么从该位置开始向后所有位置就不需要考虑了。
代码实现(C++,时间复杂度为O(N^2)):
//方法二:排序+双指针
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> vv; //存储满足条件的三元组
//1、排升序
sort(nums.begin(),nums.end());
//2、利用双指针解决问题
int n=nums.size();
for(int i=0;i<n-1;) //从前往后,控制固定值
{
int iVal = nums[i]; //记录当前固定值
if(iVal > 0) //小优化
break;
int left = i+1,right = n-1;//初始区间
while(left < right)
{
if(nums[left] + nums[right] > -nums[i]) //相加大于固定值的相反值
--right;
else if( nums[left] + nums[right] < -nums[i]) //相加小于固定值的相反值
++left;
else //相加等于固定值的相反值
{
vv.push_back({nums[left],nums[right],nums[i]});//插入满足的三元组
int leftVal = nums[left],rightVal = nums[right]; //记录此时left和right位置上的值,为去重做准备
//去重
while(left < right && nums[left] == leftVal)
++left;
while(left < right && nums[right] == rightVal)
--right;
//不直接返回继续走循环条件,防止漏数据
}
}
//防止固定值重复从而引起重复数据
while(i < n - 1 && nums[++i] == iVal); //这里更新了i的值,那么在循环中就不需要更新了
}
return vv;
}
};五、四数之和
18. 四数之和 - 力扣(LeetCode)
给你一个由
n个整数组成的数组nums,和一个目标值target。请你找出并返回满足下述全部条件且不重复的四元组[nums[a], nums[b], nums[c], nums[d]](若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target你可以按 任意顺序 返回答案 。
示例 1:
输入:nums = [1,0,-1,0,-2,2], target = 0 输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]示例 2:
输入:nums = [2,2,2,2,2], target = 8 输出:[[2,2,2,2]]提示:
1 <= nums.length <= 200-10^9 <= nums[i] <= 10^9-10^9 <= target <= 10^9
这道题和第四题差不多一样,它们的区别是由原来的三个数变为现在的四个数,由原来固定的target为0变为现在的target不固定。
它也能暴力求解(时间复杂度为O(N^4)),我们这里只讲优解,这道题的解题思路和第四题一模一样:依次固定一个数a,在a后面的区间内,利用"三数之和"的思想,找到三个数,使它们三个数相加等于target-a。"三数之和"拆分开来就是,先固定一个数b,在b后边的区间内利用"双指针"找到两个数,使它们两个数的和等于target-a-b。
这道题同样需要额外注意两点:1、去重问题 2、不漏数据
代码实现(C++,时间复杂度为O(N^3)):
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> vv; //存放满足条件的四元组
//1、排序
sort(nums.begin(), nums.end());
//2、利用双指针解决问题
int n = nums.size();
for (int i = 0;i < n - 1;) //固定a
{
//利用"三数之和"思想
for (int j = i + 1;j < n - 1;) //固定b
{
int left = j + 1, right = n - 1;//控制区间
while (left < right)
{
if (nums[left] + nums[right] > (long long)target - nums[i] - nums[j]) //如果是int类型,可能会发生越界问题,比int小值还要小,所以用long long
--right;
else if (nums[left] + nums[right] < (long long)target - nums[i] - nums[j])
++left;
else
{
vv.push_back({ nums[left],nums[right],nums[i],nums[j] });
int leftVal = nums[left], rightVal = nums[right];
//去重
while (left < right && nums[left] == leftVal)
++left;
while (left < right && nums[right] == rightVal)
--right;
}
}
//b去重
int jVal = nums[j];
while (j < n - 1 && nums[++j] == jVal);
}
//a去重
int iVal = nums[i];
while (i < n - 1 && nums[++i] == iVal);
}
return vv;
}
};(完结)