算法题总结（十）——二叉树上

news2024/11/25 1:31:35

#二叉树的递归遍历

// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();  //也可以把result 作为全局变量，只需要一个函数即可。
        
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);
        preorder(root.left, result);
        preorder(root.right, result);
    }
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        inorder(root, res);
        return res;
    }

    void inorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        inorder(root.left, list);
        list.add(root.val);             // 注意这一句
        inorder(root.right, list);
    }
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        postorder(root, res);
        return res;
    }

    void postorder(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        postorder(root.left, list);
        postorder(root.right, list);
        list.add(root.val);             // 注意这一句
    }
}

后面写二叉树的递归算法，****就是要注意1、采用什么递归遍历 2、对结点的处理逻辑

一般是中左右，对中结点进行处理。

如果需要用到左右结点的返回值的，使用后续遍历，左右中。

#二叉树的迭代遍历

前序和中序是完全两种代码风格，这是因为前序遍历中访问节点（遍历节点）和处理节点（将元素放进result数组中）可以同步处理****，但是中序就无法做到同步！

对于中序遍历可以用一个指针来访问节点，访问到最底层，每次将访问的节点放进栈，如果访问到了最底层，将访问的节点放进栈。

再来看后序遍历，先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了。

二叉树的非递归遍历要使用栈。

// 前序遍历顺序：中-左-右，入栈顺序：中-右-左
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;  //返回空链表
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.right != null){
                stack.push(node.right);
            }
            if (node.left != null){
                stack.push(node.left);
            }
        }
        return result;
    }
}

// 中序遍历顺序: 左-中-右 入栈顺序： 左-右
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
            if (cur != null){   // 指针来访问节点，访问到最底层
                stack.push(cur);  // 指针来访问节点，访问到最底层  不等于空，入栈并指向左孩子
                cur = cur.left;
            }else{               //从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                cur = stack.pop();
                result.add(cur.val); //中
                cur = cur.right;  //右
            }
        }
        return result;
    }
}

// 后序遍历顺序 左-右-中 入栈顺序：中-左-右 出栈顺序：中-右-左， 最后翻转结果
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.left != null){   //先放左子树，再放右子树
                stack.push(node.left);
            }
            if (node.right != null){
                stack.push(node.right);
            }
        }
        Collections.reverse(result);  
        return result;
    }
}

二叉树的层序遍历

102、二叉树的层序遍历

一层一层的处理

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {

        List<List<Integer>> result= new ArrayList<>();
        if(root==null)  return result;
        Queue<TreeNode> queue =new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty())  //控制层数
        {
            List<Integer> tmp=new ArrayList<>();  //每次都新建一个ArrayList  防止被修改
            int len=queue.size();  //每层的个数
            while(len>0)  //遍历每层的结点，也可以使用for循环
            {
                TreeNode node =queue.poll();
                tmp.add(node.val);
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                len--;
            }
            result.add(tmp);
        }
        return result;
    }
}

#107、二叉树的层序遍历二

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

示例 1：

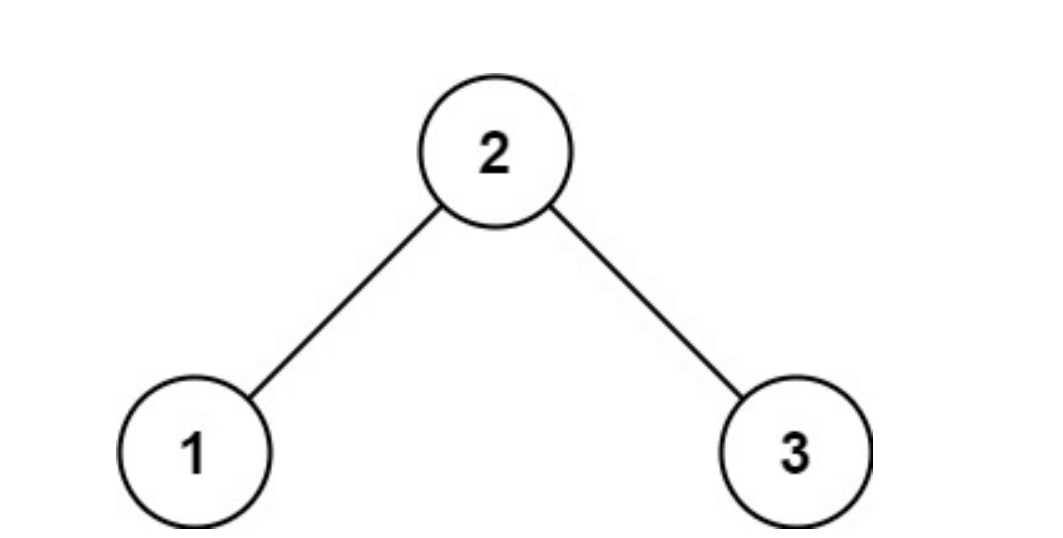
输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

把每层的列表从头插入结果中就可以

class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> ans= new ArrayList<List<Integer>>();
        if(root==null) return ans;
        Queue<TreeNode> queue =new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty())
        {
            List<Integer> tmp= new ArrayList<>();
            int len=queue.size();
            while(len>0)
            {
                TreeNode node =queue.poll();
                tmp.add(node.val);
                if(node.left!=null) 
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                len--;
            }
            ans.add(0,tmp);  //每次都从头开始插入
        }
        return ans;

    }
}

#199、二叉树的右视图

给定一个二叉树的 根节点root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

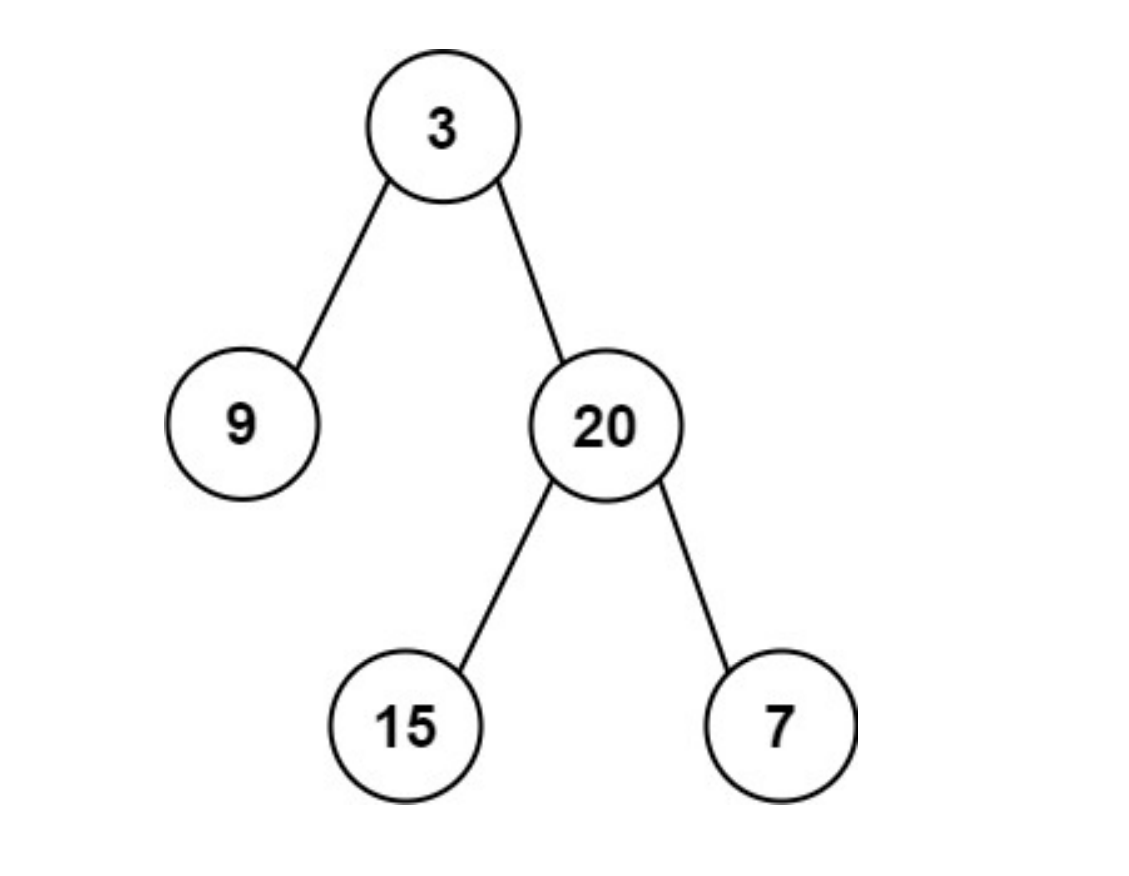
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

即利用队列的长度，把每一层的最后一个结点加入结果中

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        //即看到的都是每一层的最后一个结点
        List<Integer> ans =new ArrayList<>();
        Queue<TreeNode> queue =new LinkedList<>();
        if(root==null) return ans; //一定要判断为空的情况，否则会空指针异常
        queue.add(root);
        while(!queue.isEmpty())
        {
            int len =queue.size();
            while(len>0)
            {
                TreeNode node =queue.poll();
                if(len==1) 
                    ans.add(node.val);  //把每一层的最后一个结点加入
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                len--;
            }

        }
        return ans;
    }
}

637、二叉树的层平均值

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

示例 1：

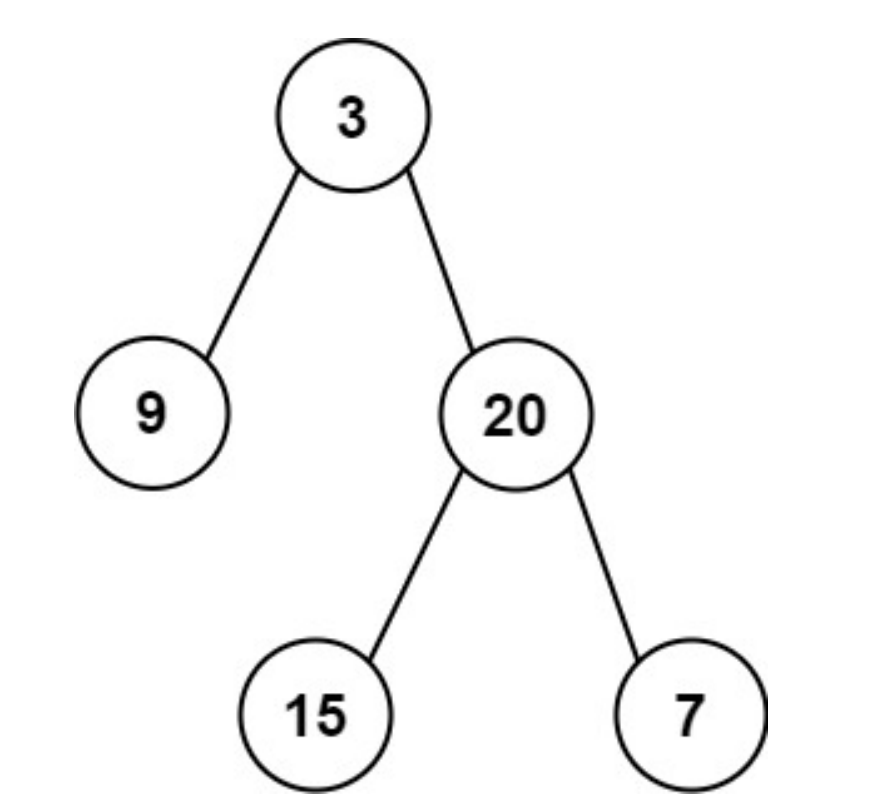
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

使用一个sum来计算每层的和

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> ans =new ArrayList<>();
        Queue<TreeNode> queue =new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty())
        {
            int len =queue.size();
            int n=len;
            double sum=0;
            while(len>0)
            {
                TreeNode node =queue.poll();
                sum += node.val;
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                len--;
            }
            ans.add(sum/n);
        }
        return ans;
    }
}

429、N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

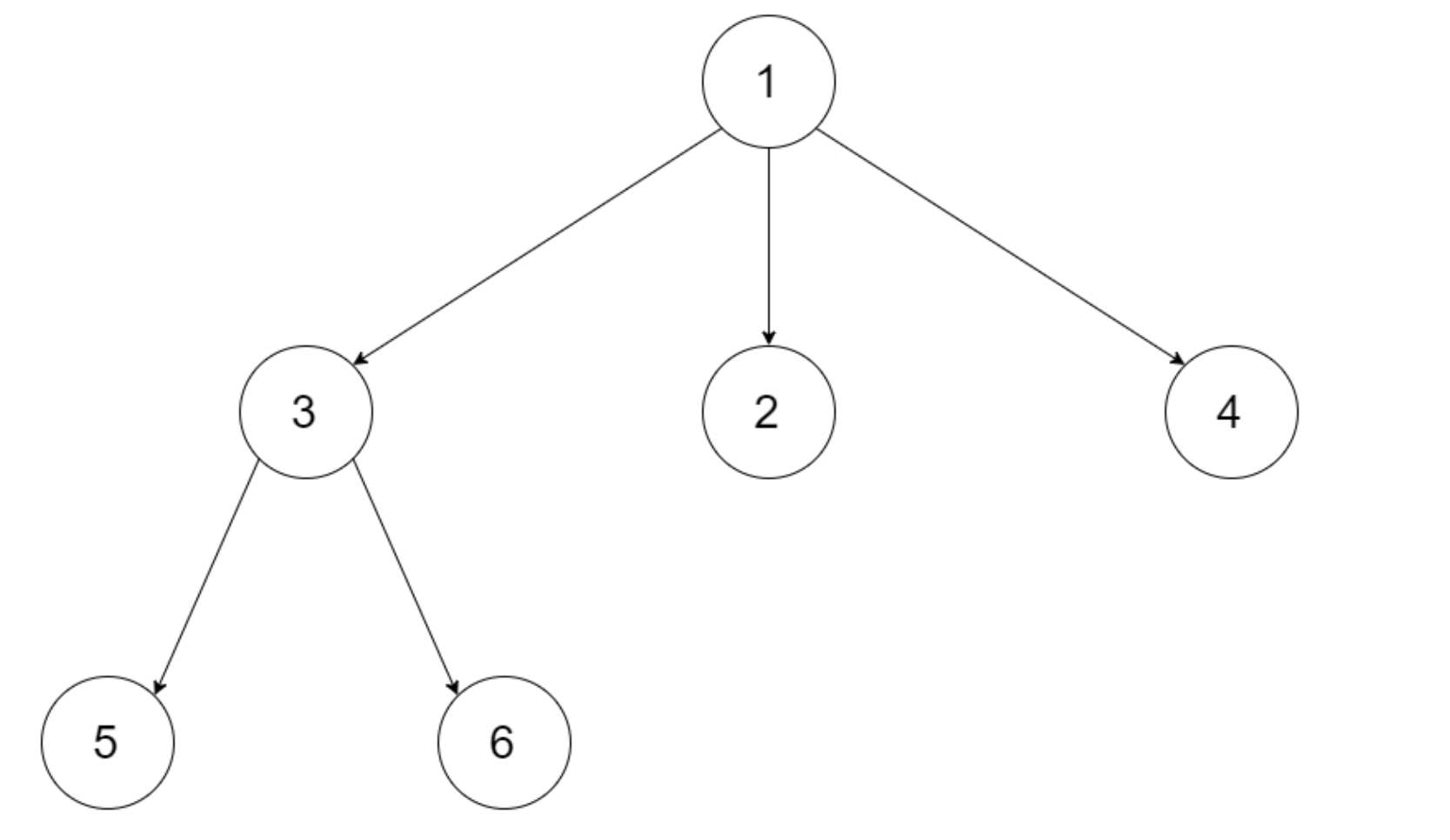
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

class Solution {
    public List<List<Integer>> levelOrder(Node root) {

        List<List<Integer>> ans= new ArrayList<List<Integer>>();
        Queue<Node> queue = new LinkedList<>();
        if(root==null) return ans;
        queue.add(root);
        while(!queue.isEmpty())
        {
            int len =queue.size();
            List<Integer> tmp=new ArrayList<>();
            while(len>0)
            {
                Node node =queue.poll();
                tmp.add(node.val);
                len--;
                List<Node> childrens =node.children;
                for(Node c:childrens)
                {
                    if(c!=null) 
                        queue.add(c);
                }

            }
            ans.add(tmp);
        }
        return ans;   
    }
}

515、找出每层的最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

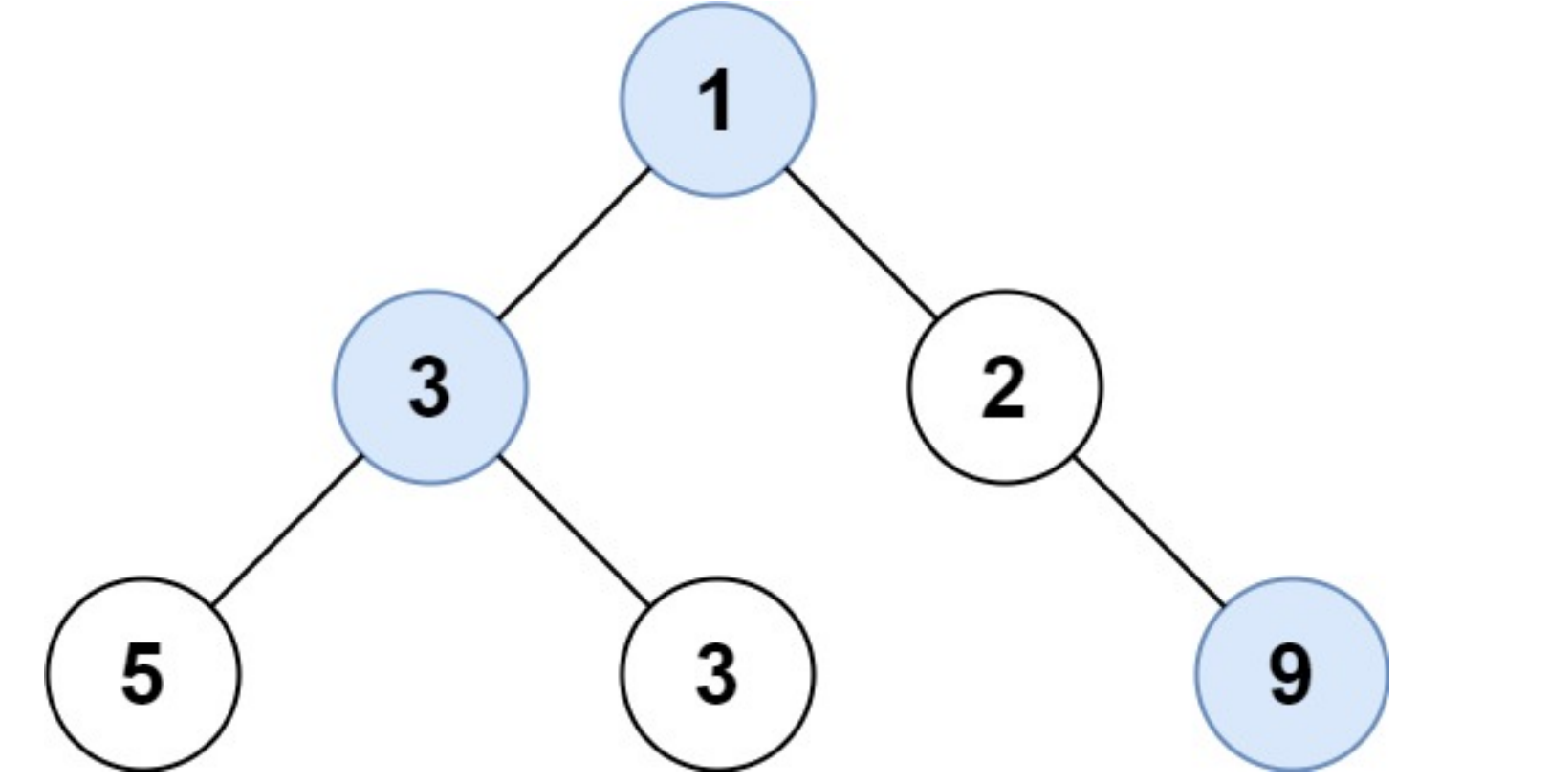
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

class Solution {
    public List<Integer> largestValues(TreeNode root) {
        List<Integer> ans =new ArrayList<>();
        if(root==null) return ans;
        Queue<TreeNode> queue =new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty())
        {
            int len =queue.size();
            int max=Integer.MIN_VALUE; //记录每一层的最大值
            while(len>0)
            {
                TreeNode node = queue.poll();
                if(node.val>max)
                    max=node.val;
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                len--;
            }
            ans.add(max);
        }
        return ans;


    }
}

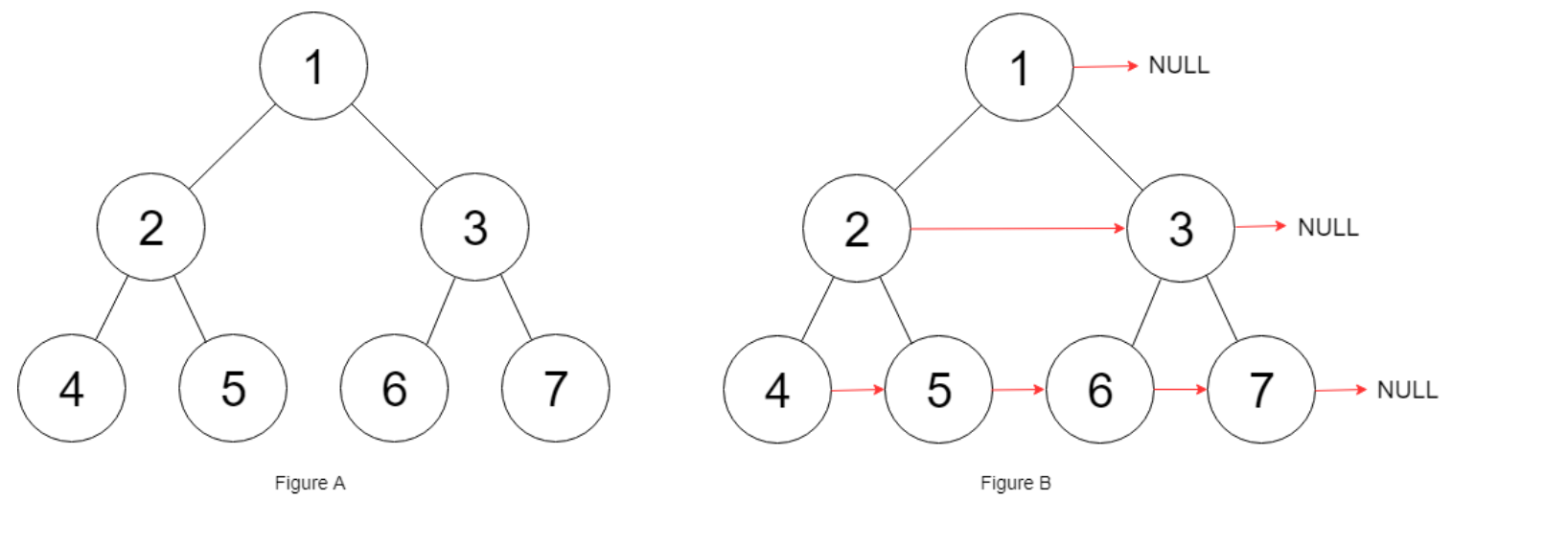
116、填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
    int val;
    Node *left;
    Node *right;
    Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

class Solution {
    public Node connect(Node root) {
        Queue<Node> queue =new LinkedList<>();
        if(root==null)  return root;
        queue.add(root);
        while(!queue.isEmpty())
        {
            int len =queue.size();
            while(len>0)
            {   
                Node node = queue.poll();  //本质上还是找到每层的最后一个结点
                if(len==1)
                {
                    node.next=null;
                }
                else
                {
                    Node nextNode =queue.peek();
                    node.next=nextNode;
                }
                len--;
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
            }
        }
        return root;
    }
}

#104、 二叉树的最大深度

使用前序求的就是深度，使用后序呢求的是高度

层序遍历：

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int hight=0;
        while(!queue.isEmpty())
        {
            int len=queue.size();
            while(len>0)
            {
                TreeNode node =queue.poll();
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                len--;
            }
            hight++;

        }
        return hight;


    }
}

后续遍历：

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null) return 0;
        int leftDepth =maxDepth(root.left); //左
        int rightDepth =maxDepth(root.right);  //右

        return Math.max(leftDepth,rightDepth)+1; //中

    }
}

前序遍历：

class Solution {
    public:
    int result;//使用result来记录最大深度
    void getDepth(TreeNode* node, int depth) {
        result = depth > result ? depth : result; // 中
        if (node->left == NULL && node->right == NULL) return ;
        if (node->left) { // 左
            getDepth(node->left, depth + 1);
        }
        if (node->right) { // 右
            getDepth(node->right, depth + 1);
        }
        return ;
    }
    int maxDepth(TreeNode* root) {
        result = 0;
        if (root == 0) return result;
        getDepth(root, 1);
        return result;
    }
};

101、 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

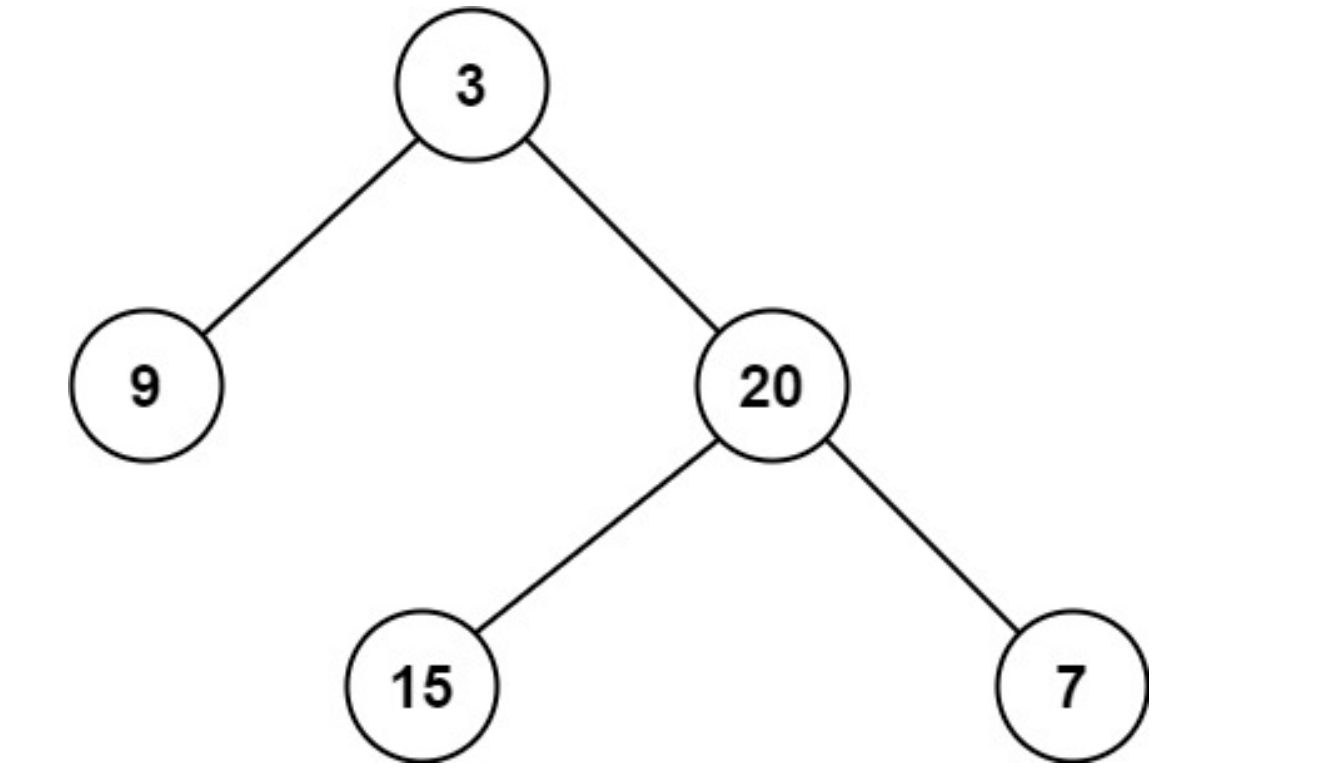
输入：root = [3,9,20,null,null,15,7]
输出：2

即当左右孩子都为空的时候就返回

层序遍历

class Solution {
    public int minDepth(TreeNode root) {
        if(root==null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int depth=0;
        while(!queue.isEmpty())
        {
            int len=queue.size();
            depth++;
            while(len>0)
            {

                TreeNode node =queue.poll();
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                if(node.right==null && node.left==null)
                    return depth;
                len--;
            }

        }
        return depth;

    }
}

递归法

如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

class Solution {
    //递归法
    public int minDepth(TreeNode root) {
        if(root==null) return 0;
        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);
        if(root.left==null)
            return rightDepth+1; //否则没有左孩子的分支会被当成最小值
        if(root.right==null)
            return leftDepth+1;
        return Math.min(leftDepth,rightDepth)+1;

    }
}

#226、翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

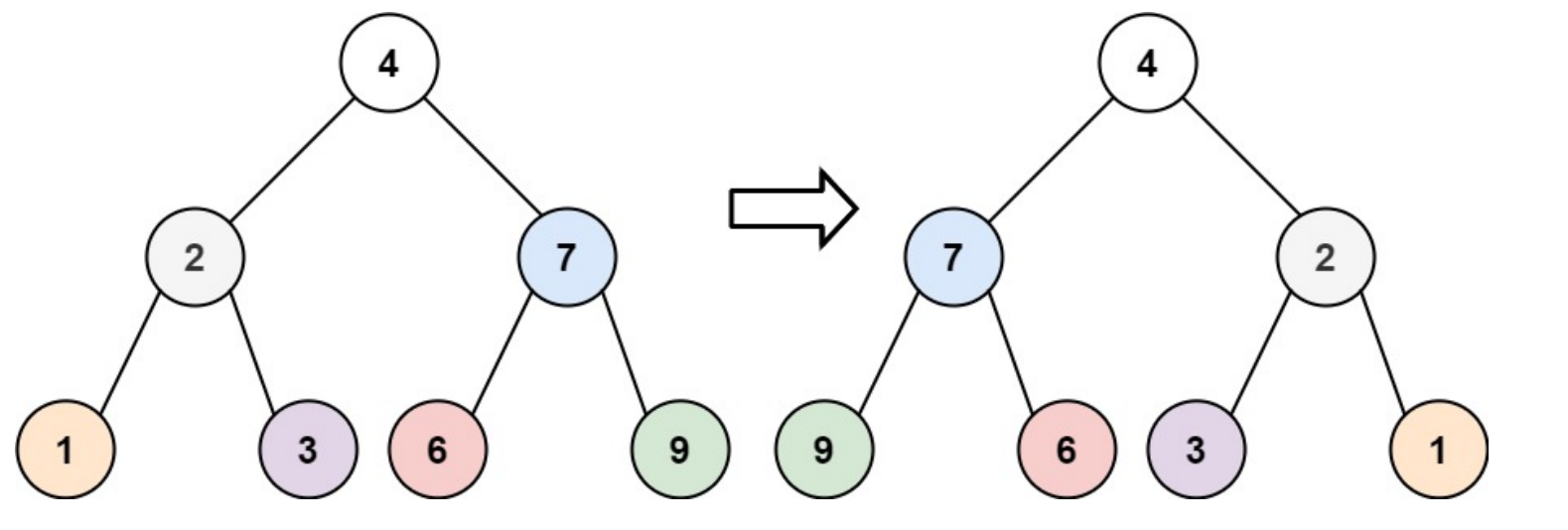
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

采用层序遍历，每取出一个结点就交换其左右孩子

class Solution {
    public TreeNode invertTree(TreeNode root) {
        //采用层序遍历
        Queue<TreeNode> queue =new LinkedList<>();
        if(root==null)  
            return root;
        queue.add(root);
        while(!queue.isEmpty())
        {
            int len =queue.size();
            while(len>0)
            {
                TreeNode node=queue.poll();
                TreeNode tmp =node.right;
                node.right=node.left;
                node.left=tmp;
                if(node.left!=null) queue.add(node.left);
                if(node.right!=null) queue.add(node.right);
                len--;
            }
        }
        return root;
    }
}

递归法：

对一个结点交换左右，然后进行左右递归

class Solution {
    /**
     * 前后序遍历都可以
     * 中序不行，因为先左孩子交换孩子，再根交换孩子（做完后，右孩子已经变成了原来的左孩子），再右孩子交换孩子（此时其实是对原来的左孩子做交换）
     */
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        invertTree(root.left);
        invertTree(root.right);
        swapChildren(root);    //也可以中左右
        return root;
    }

    private void swapChildren(TreeNode root) {
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}

#114、二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

  • 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
  • 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

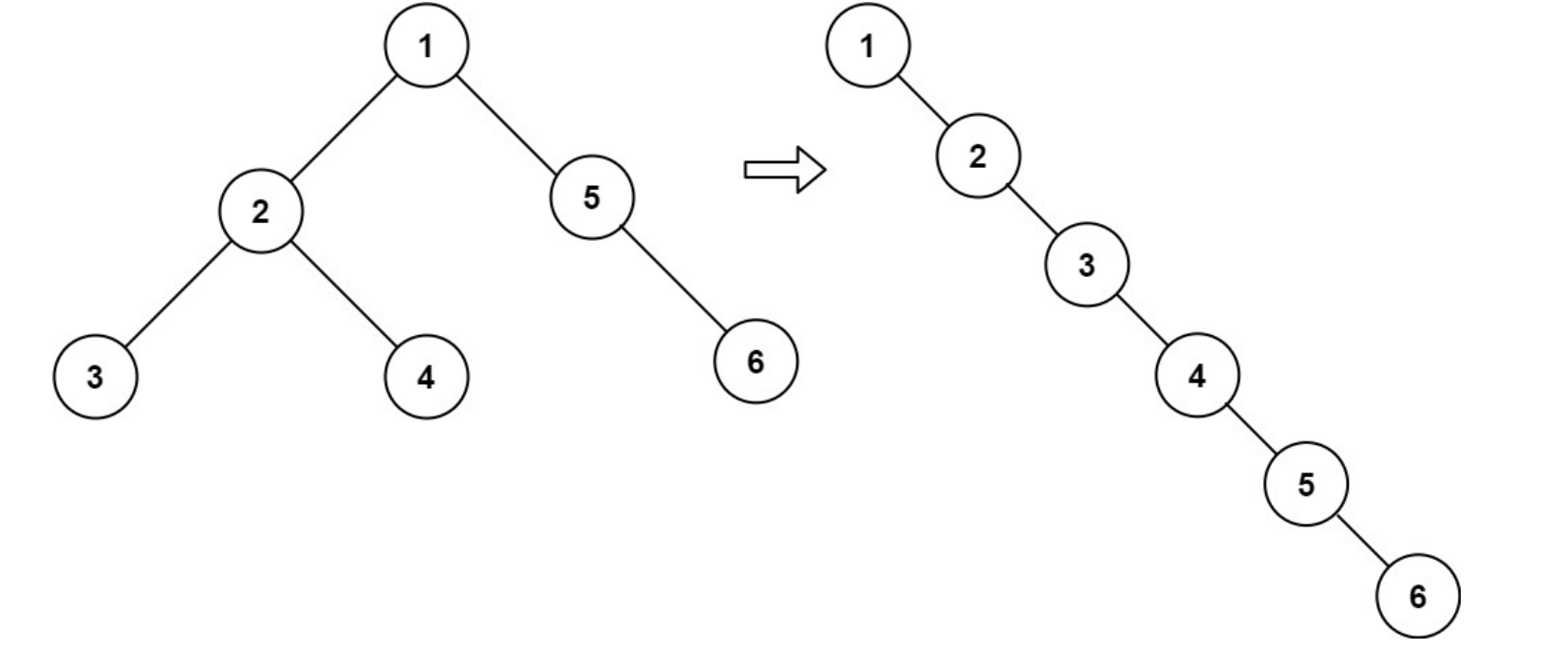
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

class Solution {
    //保存前序遍历的结果
    List<TreeNode> list=new ArrayList<>();
    public void flatten(TreeNode root) {
        preorder(root);
        for(int i=1;i<list.size();i++)
        {
            TreeNode pre=list.get(i-1);
            TreeNode cur=list.get(i);
            pre.left=null;
            pre.right=cur;
        }

    }
    //构造树，然后值是结点
    public void preorder(TreeNode root)
    {
        if(root==null)
            return;
        list.add(root);
        preorder(root.left);
        preorder(root.right);
    }
}

递归+回溯的思路，将前序遍历反过来遍历，那么第一次访问的就是前序遍历中最后一个节点。那么可以调整最后一个节点，再将最后一个节点保存到pre里，再调整倒数第二个节点，将它的右子树设置为pre，再调整倒数第三个节点，依次类推直到调整完毕。和反转链表的递归思路是一样的。

class Solution {
    //反前序遍历
    TreeNode pre;
    public void flatten(TreeNode root) {
        if(root==null)
            return;
        flatten(root.right);
        flatten(root.left);
        //先找到最后一个结点，然后记录
        root.left=null;
        root.right=pre;
        pre=root;
    }

}

#101、对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

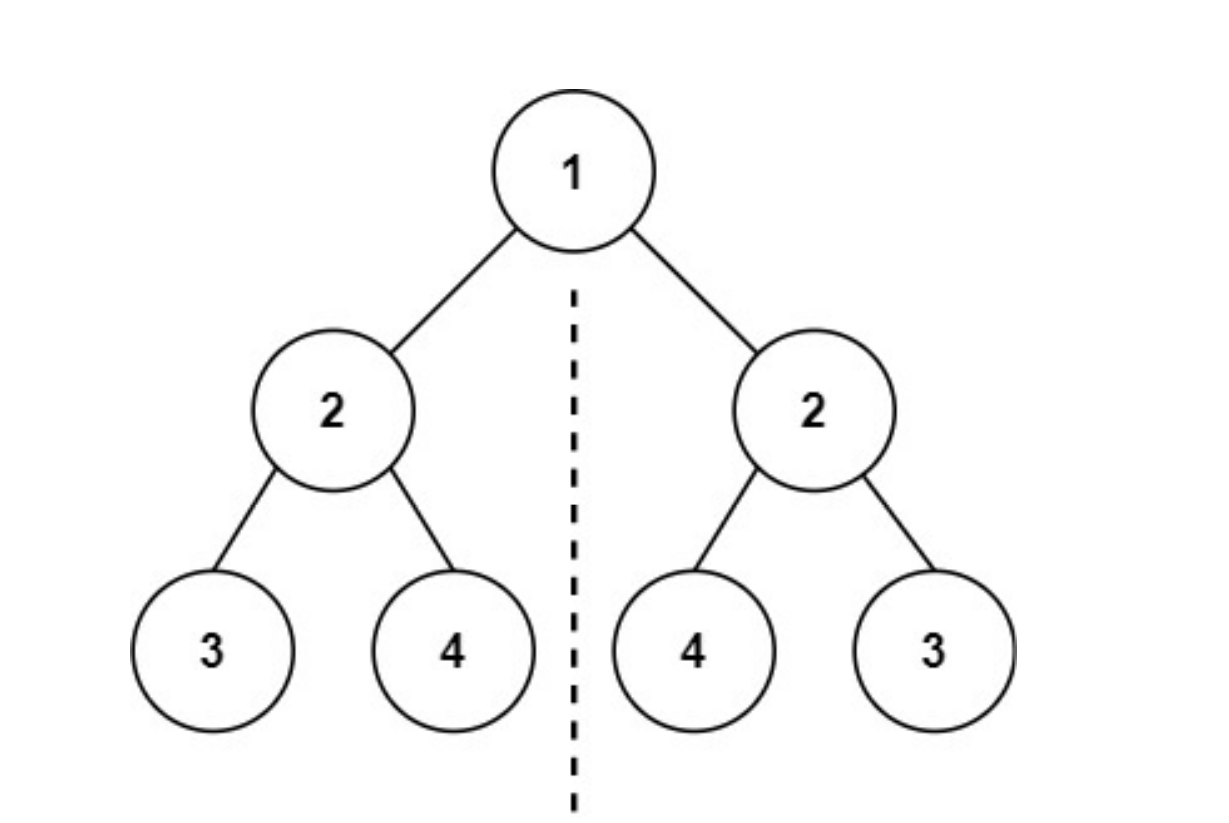
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

使用一个队列，类似于层序遍历的方式，只不过不用加len来判断层数，并且空结点也要入队。

而本题的迭代法中我们使用了队列，需要注意的是这不是层序遍历，而且仅仅通过一个容器来成对的存放我们要比较的元素，

class Solution {
    public boolean isSymmetric(TreeNode root) {
        //把空节点也看成结点
        Queue<TreeNode> queue =new LinkedList<>();
        queue.add(root.left);
        queue.add(root.right);
        while(!queue.isEmpty())
        {
            //不符合就返回false
            TreeNode leftnode =queue.poll();    //每次取出需要比较的两个结点
            TreeNode rightnode =queue.poll();    //每次取出需要比较的两个结点
            if(leftnode==null && rightnode ==null)
                continue;
            if(leftnode==null||rightnode==null||leftnode.val!=rightnode.val)
                return false;

            queue.add(leftnode.left);
            queue.add(rightnode.right);
            queue.add(leftnode.right);
            queue.add(rightnode.left);
        }

        return true;

    }
}

递归法：

class Solution {
    private boolean copmare(TreeNode leftnode, TreeNode rightnode)
    {
        if(leftnode==null && rightnode!=null) return false;
        else if(leftnode!=null && rightnode==null) return false;
        else if(leftnode==null && rightnode==null) return true;
        else if(leftnode.val!=rightnode.val) return false;    //也可以合在一起判断
        else  //说明leftnode和rightnode相等
            return copmare(leftnode.left,rightnode.right) && copmare(leftnode.right,rightnode.left);

    }
    public boolean isSymmetric(TreeNode root) {
        return copmare(root.left,root.right);

    }
}

100、相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

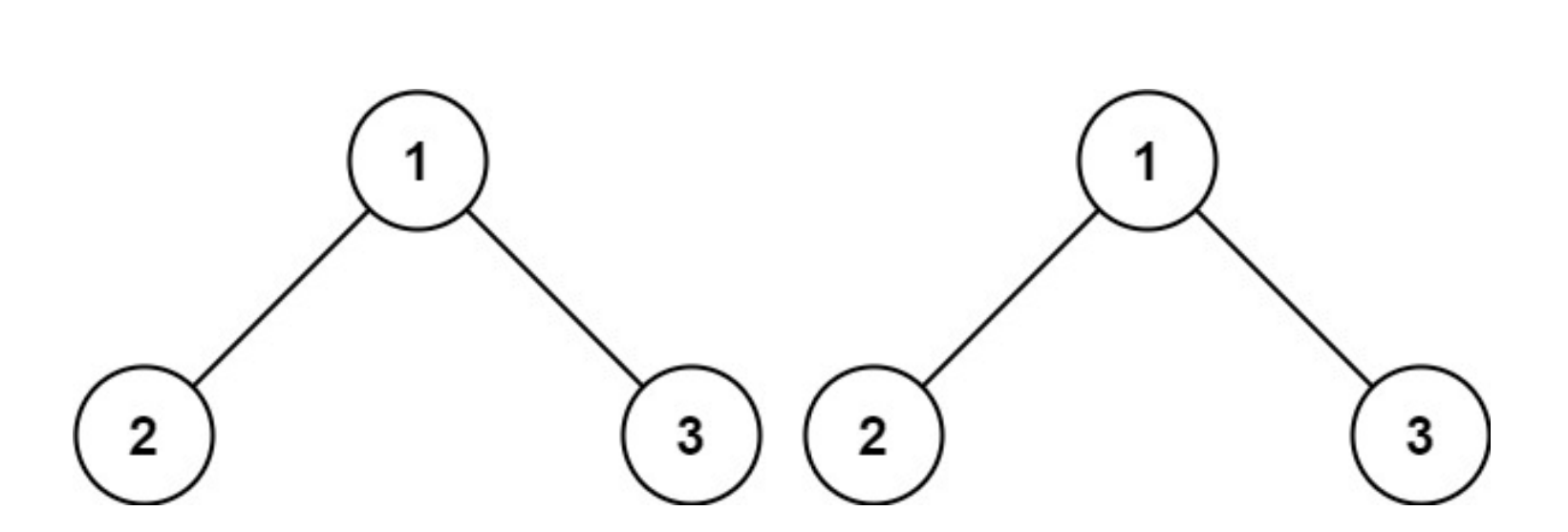
输入：p = [1,2,3], q = [1,2,3]
输出：true

和对称二叉树一样

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //使用同一个队列
        Queue<TreeNode> queue =new LinkedList<>();
        queue.add(p);
        queue.add(q);
        while(!queue.isEmpty())
        {

            TreeNode node1 =queue.poll();
            TreeNode node2 =queue.poll();
            if(node1==null && node2==null)
                continue;
            else if(node1==null &&node2!=null)
                return false;
            else if(node1!=null && node2==null)
                return false;
            else if(node1.val!=node2.val)
                return false;

            queue.add(node1.left);
            queue.add(node2.left);
            queue.add(node1.right);
            queue.add(node2.right);
        }
        return true;

    }
}

递归法

class Solution {
    //递归法：求树是否相等
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p==null&& q==null) return true;
        else if(p==null &&q!=null) return false;
        else if(p!=null &&q==null) return false;
        else if(p.val!=q.val) return false;
        else  //即结点相同，判读左右结点
        {
            return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
        }


    }
}

572、另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

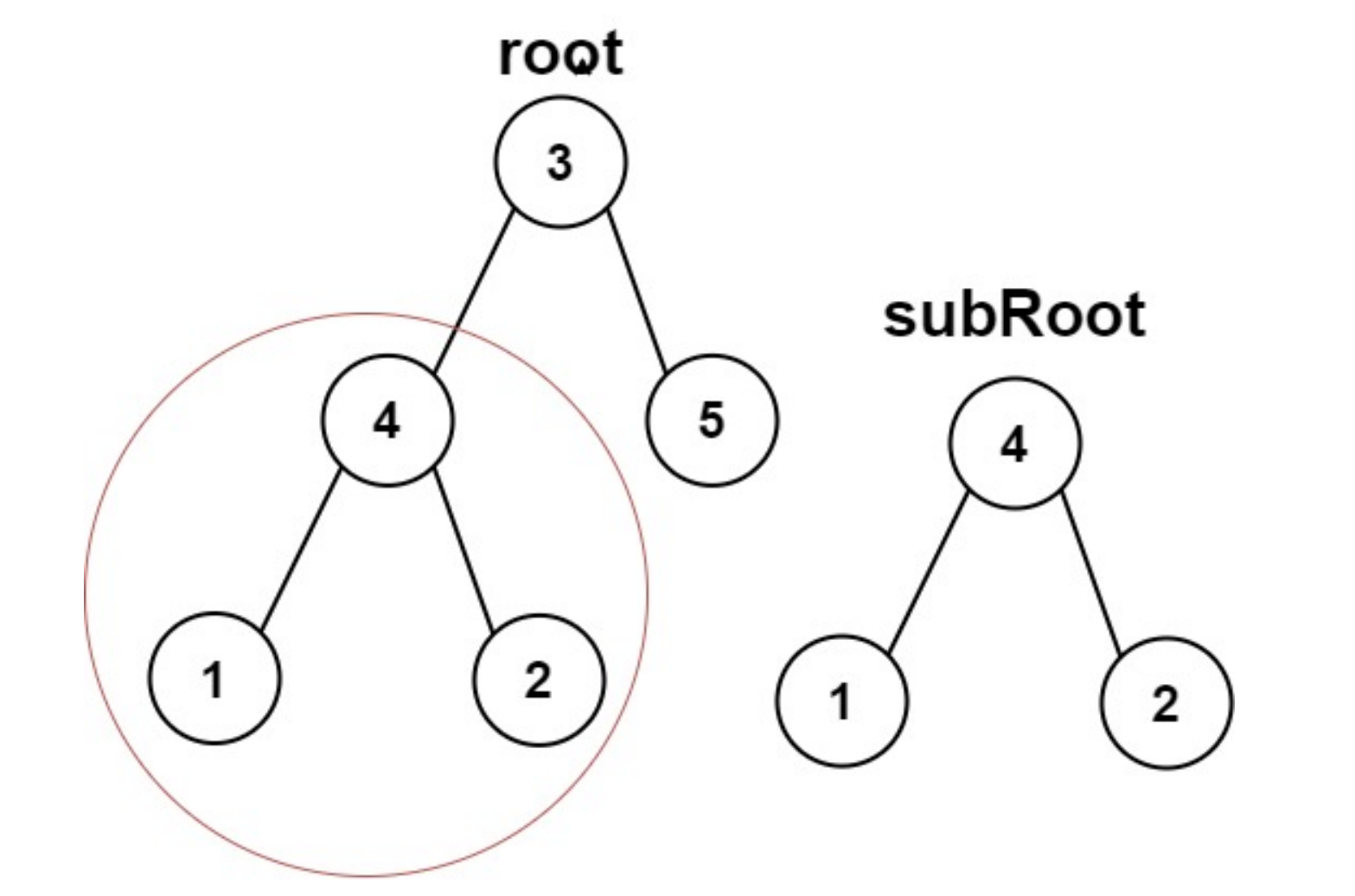
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

采用遍历+判断树是否相等

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q)
    {
        if(p==null && q==null)  return true;
        else if(p==null||q==null||p.val!=q.val)  return false;  //直接合在一起写
        else{ //说明结点值相同
            return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
        }
    }
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        Queue<TreeNode> queue =new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty())
        {
            TreeNode node =queue.poll();
            if(isSameTree(node,subRoot))
                return true;
            if(node.left!=null) queue.add(node.left);
            if(node.right!=null) queue.add(node.right);
        }
        return false;

    }
}

559、n叉树的最大深度

class Solution {
    /*递归法，后序遍历求root节点的高度*/
    public int maxDepth(Node root) {
        if (root == null) return 0;  //递归出口

        int depth = 0;
        if (root.children != null){
            for (Node child : root.children){
                depth = Math.max(depth, maxDepth(child));
            }
        }

        return depth + 1; //中节点
    }  
}

#110、平衡二叉树

在递归法求高度的基础上，每次递归要判断是否是平衡二叉树。

class Solution {  //递归法求高度，因为是求高度，所以是后序遍历：左右中
    private int getHight(TreeNode root)
    {
        if(root==null) return 0;
        int leftHight=getHight(root.left);
        if(leftHight==-1) 
            return -1;    //用-1代表不是平衡二叉树
        int rightHight=getHight(root.right);
        if(rightHight==-1) 
            return -1;

        if(Math.abs(leftHight-rightHight)>1)
            return -1;
        return Math.max(leftHight,rightHight)+1;
    }
    public boolean isBalanced(TreeNode root) {
        if(getHight(root)==-1) return false;
        else
            return true;

    }
}

层序遍历

class Solution {  //层次遍历求高度

    private int getHigth(TreeNode root) {
        if(root==null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int hight=0;
        while(!queue.isEmpty())
        {
            int len=queue.size();
            while(len>0)
            {
                TreeNode node =queue.poll();
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                len--;
            }
            hight++;
        }
        return hight;
    }

    //层次遍历判断
    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty())
        {
            int len=queue.size();
            while(len>0)
            {
                TreeNode node =queue.poll();
                int leftHight =getHigth(node.left);
                int rightHight =getHigth(node.right);
                if(Math.abs(leftHight-rightHight)>1)
                    return false;
                if(node.left!=null)
                    queue.add(node.left);
                if(node.right!=null)
                    queue.add(node.right);
                len--;
            }
        }
        return true;

    }
}

#543、二叉树的直径

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

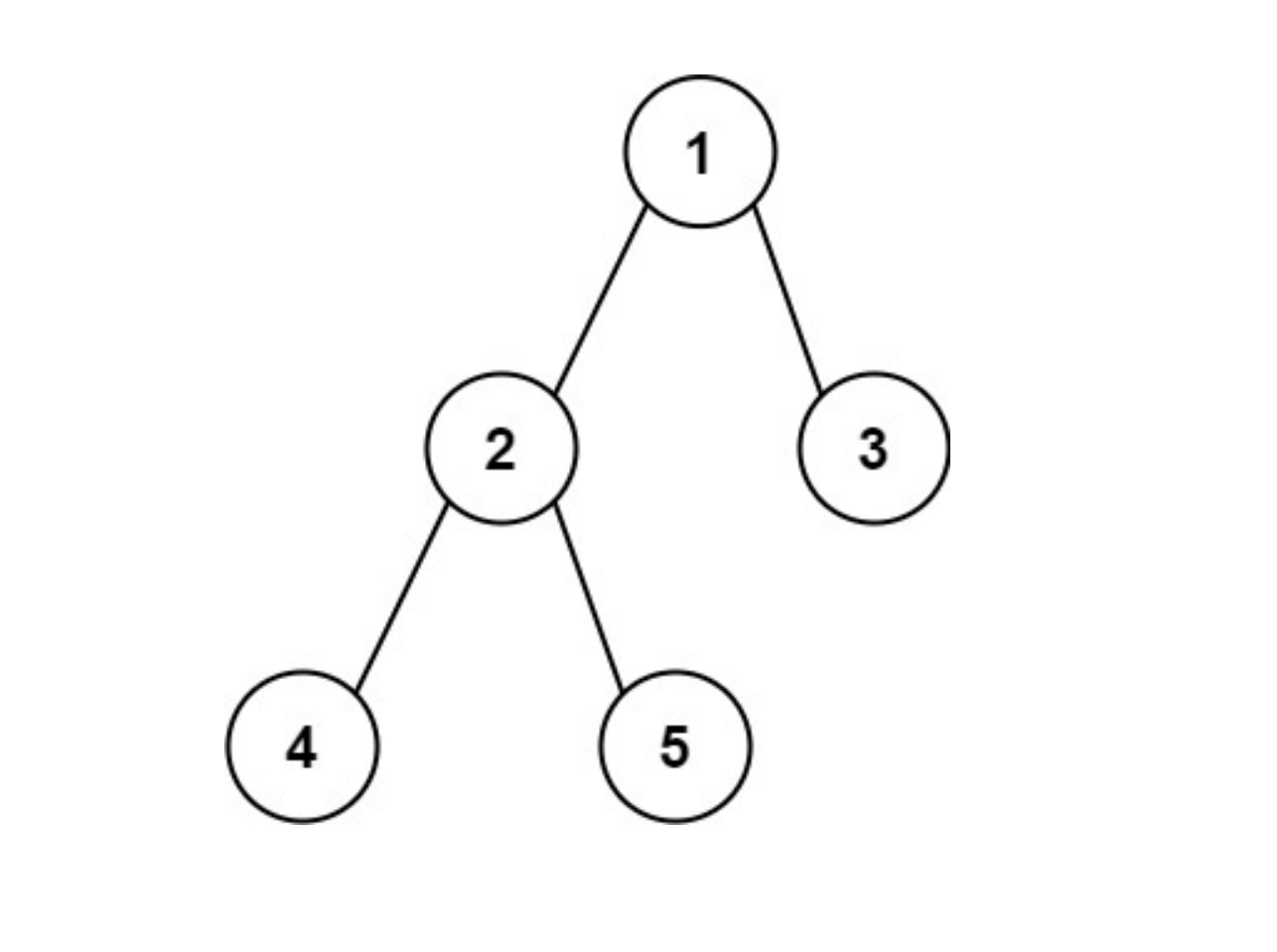
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

一开始以为就是根节点的左右子树的深度之和，后来发现最长路径不一定经过根结点。

class Solution {
    //直径，即树中找最长路径，最长路径不一定经过根结点
    //对于经过的每一个结点来说，最长路径就是左右子树的深度 之和
    int maxd=0;  //记录最大直径
    public int diameterOfBinaryTree(TreeNode root) {
        height(root);
        return maxd; 
    }

    //递归求深度
    public int height(TreeNode root)
    {
        if(root==null)
            return 0;
        int left=height(root.left);
        int right=height(root.right);
        //在遍历的过程中找以每个结点为根的最大直径
        maxd=Math.max(maxd,left+right); //将每个节点最大直径(左子树深度+右子树深度)当前最大值比较并取大者
        return Math.max(left,right)+1;  //返回结点深度
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2195433.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

公开数据集网站分享

公开数据集网站分享

参考链接&#xff1a;常用的医学组织切片细胞图像数据集_细胞分割数据集-CSDN博客文章浏览阅读1.3w次&#xff0c;点赞32次&#xff0c;收藏133次。乳腺癌细胞图像数据集、血细胞图像数据集、HE染色切片、疟疾细胞图像图像识别、分类、分割_细胞分割数据集https://blog.csdn.ne…
阅读更多...
Redis list 类型

Redis list 类型

list类型 类型介绍 列表类型 list 相当于 数组或者顺序表 list内部的编码方式更接近于 双端队列 &#xff0c;支持头插 头删 尾插 尾删。 需要注意的是&#xff0c;Redis的下标支持负数下标。 比如数组大小为5&#xff0c;那么要访问下标为 -2 的值可以理解为访问 5 - 2 3 …
阅读更多...
Linux dlsym和直接调用函数地址解析分析

Linux dlsym和直接调用函数地址解析分析

dlsym 函数是 Linux 下动态链接库&#xff08;shared library&#xff09;编程中的一个重要函数。它用于在运行时获取动态链接库中符号的地址&#xff0c;通常用于获取函数指针或变量的地址。 以下是 dlsym 函数的基本用法和示例。 1. 函数原型 void *dlsym(void *handle, c…
阅读更多...
【超详细】基于YOLOv11的PCB缺陷检测

【超详细】基于YOLOv11的PCB缺陷检测

主要内容如下&#xff1a; 1、数据集介绍 2、下载PCB数据集 3、不同格式数据集预处理&#xff08;Json/xml&#xff09;&#xff0c;制作YOLO格式训练集 4、模型训练及可视化 5、Onnxruntime推理 运行环境&#xff1a;Python3.8&#xff08;要求>3.8&#xff09;&#xff…
阅读更多...
ubuntu ssh远程执行k8s命令报错the connection to the server localhost:8080 was refused

ubuntu ssh远程执行k8s命令报错the connection to the server localhost:8080 was refused

修改前&#xff1a; ssh root192.168.31.167 kubectl apply -f /root/jenkinsexcute/saas.demo.api.k8s.yml --recordecho "export KUBECONFIG/etc/kubernetes/admin.conf" >> /root/.bashrc 修改后 添加一段&#xff1a;export KUBECONFIG/etc/kubernetes/a…
阅读更多...
【专题】操作系统概述

【专题】操作系统概述

1. 操作系统的目标和作用 操作系统的目标与应用环境有关。 在查询系统中所用的OS&#xff0c;希望能提供良好的人—机交互性&#xff1b; 对于应用于工 业控制、武器控制以及多媒体环境下的OS&#xff0c;要求其具有实时性&#xff1b; 对于微机上配置的OS&#xff0c;则更看…
阅读更多...
什么是强基计划？

什么是强基计划？

“强基计划”是中国教育部于2020年推出的一项全新的高等教育招生改革计划&#xff0c;旨在通过更加科学、公正的选拔机制&#xff0c;选拔出有志于基础学科并具备扎实学科功底、创新潜质的优秀学生&#xff0c;从而推动国家基础学科的发展&#xff0c;提升自主创新能力。与传统…
阅读更多...
【自动驾驶】UniAD代码解析

【自动驾驶】UniAD代码解析

1.参考 论文&#xff1a;https://arxiv.org/pdf/2212.10156 代码&#xff1a;https://github.com/OpenDriveLab/UniAD 2.环境配置 docs/INSTALL.md &#xff08;1&#xff09;虚拟conda环境 conda create -n uniad python3.8 -y conda activate uniad &#xff08;2&#…
阅读更多...
微信小程序和抖音小程序的分享和广告接入代码

微信小程序和抖音小程序的分享和广告接入代码

开发完成小程序或者小游戏之后&#xff0c;我们为什么要接入分享和广告视频功能&#xff0c;主要原因有以下几个方面。 微信小程序和抖音小程序接入分享和广告功能主要基于以下几个原因&#xff1a; 用户获取与增长&#xff1a;分享功能可以帮助用户将小程序内容传播给更多人&…
阅读更多...
C语言刷题--有关闰年

C语言刷题--有关闰年

满足以下一种即是闰年 能被4整除&#xff0c;但不能被100整除能被400整除 //输入年&#xff0c;月&#xff0c;输出该月的天数 //1月 31,28,31,30,31,30,31,31,30,31,30,31int is_leap_year(int y) {if (((y % 4 0) && (y % 100 ! 0)) || y % 400 0)return 1;return…
阅读更多...
步进电机和步进电机驱动器详解

步进电机和步进电机驱动器详解

一、步进电机的概念 步进电机是通过步进电机配套的驱动器&#xff0c;将控制器传来的脉冲信号转换成角位移的开环电机&#xff08;没有反馈&#xff09;。 步进电机工作时的位置和速度信号不反馈给控制系统&#xff0c;如果电机工作时的位置和速度信号反馈给控制系统&#xff…
阅读更多...
《从零开始大模型开发与微调》真的把大模型说透了！零基础入门一定要看！

《从零开始大模型开发与微调》真的把大模型说透了！零基础入门一定要看！

2022年底&#xff0c;ChatGPT震撼上线&#xff0c;大语言模型技术迅速“席卷”了整个社会&#xff0c;人工智能技术因此迎来了一次重要进展。与大语言模型相关的研发岗薪资更是水涨船高&#xff0c;基本都是5w月薪起。很多程序员也想跟上ChatGPT脚步&#xff0c;今天给大家带来…
阅读更多...
apache.poi读取.xls文件时The content of an excel record cannot exceed 8224 bytes

apache.poi读取.xls文件时The content of an excel record cannot exceed 8224 bytes

目录 问题描述版本定位&#xff1a;打印size最大的Record定位&#xff1a;RefSubRecord解决代码 问题描述 使用apache.poi读取.xls文件时有The content of an excel record cannot exceed 8224 bytes的报错。待读取的文件的内容也是通过apache.poi写入的&#xff0c;我的文件修…
阅读更多...
【sqlmap】sqli-labs速通攻略

【sqlmap】sqli-labs速通攻略

sqli-labs工具速通 Less-1 sqlmap -u http://127.0.0.1:8081/Less-1/?id1 --batch --dbs sqlmap -u http://127.0.0.1:8081/Less-1/?id1 --batch -D security --tables sqlmap -u http://127.0.0.1:8081/Less-1/?id1 --batch -D security -T users --columns sqlmap -u ht…
阅读更多...
购物清单 | 双十一加购率最高好物合集，数码购物车必备！

购物清单 | 双十一加购率最高好物合集，数码购物车必备！

​双十一来临&#xff0c;小伙伴们肯定已经被种草了很多很多清单&#xff0c;开始买买买了&#xff01;但是&#xff0c;作为一个数码博主&#xff0c;怎么能少了数码产品&#xff01;今天我给大家准备了一份数码人专属的购物清单&#xff0c;快来看看吧&#xff01; 运动耳机…
阅读更多...
[水墨：创作周年纪念] 特别篇！

[水墨：创作周年纪念] 特别篇！

本篇是特别篇&#xff01;&#xff01; 个人主页水墨不写bug // _ooOoo_ // // o8888888o // // 88" . "88 …
阅读更多...
如何方便地打出「」和『』

如何方便地打出「」和『』

比起英文中的引号 ‘’和 “”&#xff0c;我更喜欢使用中文直角引号&#xff1a;「」和 『』。 此外&#xff0c;在港澳台、日本这几个地区中&#xff0c;就经常使用『』和「」&#xff1a; ​ ‍ 注意&#xff1a;不同地区的习惯可能有所不同。在汉语中『』、「」分别为双…
阅读更多...
数学公式编辑器免费版下载，mathtype和latex哪个好用

数学公式编辑器免费版下载，mathtype和latex哪个好用

选择适合自己的公式编辑器需要考虑多个因素。首先&#xff0c;您需要确定编辑器支持的功能和格式是否符合您的需求&#xff0c;例如是否可以插入图片、导出各种文件格式等。其次&#xff0c;您可以考虑编辑器的易用性和界面设计是否符合您的个人喜好。另外&#xff0c;您还可以…
阅读更多...
面向对象特性中 继承详解

面向对象特性中 继承详解

目录 概念&#xff1a; 定义&#xff1a; 定义格式 继承关系和访问限定符 基类和派生类对象赋值转换&#xff1a; 继承中的作用域&#xff1a; 派生类的默认成员函数 继承与友元&#xff1a; 继承与静态成员&#xff1a; 复杂的菱形继承及菱形虚拟继承&#xff1a; 虚…
阅读更多...
手机号归属地查询-手机号归属地-手机号归属地-运营商归属地查询-手机号码归属地查询手机号归属地-运营商归属地

手机号归属地查询-手机号归属地-手机号归属地-运营商归属地查询-手机号码归属地查询手机号归属地-运营商归属地

手机号归属地查询API接口是一种网络服务接口&#xff0c;允许开发者通过编程方式查询手机号码的注册地信息。关于快证签API接口提供的手机号归属地查询服务&#xff0c;以下是一些关键信息&#xff1a; 一、快证签API接口简介 快证签API接口可能是一个提供多种验证和查询服务…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023