思维导图汇总

深度优先搜索理论基础

• 深度优先搜索（dfs）与广度优先搜索（bfs）区别：

  • dfs是可一个方向去搜，不到黄河不回头，直到遇到绝境了，搜不下去了，再换方向（换方向的过程就涉及到了回溯）。

  • bfs是先把本节点所连接的所有节点遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索方向更像是广度，四面八方的搜索过程。

• 深搜三部曲

  1. 确认递归函数，参数
  2. 确认终止条件

  if (终止条件) {
      存放结果;
      return;
  }
  

  终止添加不仅是结束本层递归，同时也是我们收获结果的时候。

  3. 处理从目前搜索节点出发的路径

  一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。

  for (选择：本节点所连接的其他节点) {
      处理节点;
      dfs(图，选择的节点); // 递归
      回溯，撤销处理结果
  }
  

汇总即：

void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

(摘自代码随想录)

98.所有可达路径(卡码网)

题目描述

给定一个有 n 个节点的有向无环图，节点编号从 1 到 n。请编写一个函数，找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。

输入描述

第一行包含两个整数 N，M，表示图中拥有 N 个节点，M 条边

后续 M 行，每行包含两个整数 s 和 t，表示图中的 s 节点与 t 节点中有一条路径

输出描述

输出所有的可达路径，路径中所有节点之间空格隔开，每条路径独占一行，存在多条路径，路径输出的顺序可任意。如果不存在任何一条路径，则输出 -1。

注意输出的序列中，最后一个节点后面没有空格！ 例如正确的答案是 1 3 5,而不是 1 3 5 ， 5后面没有空格！

输入示例

5 5
1 3
3 5
1 2
2 4
4 5

输出示例

1 3 5
1 2 4 5

提示信息

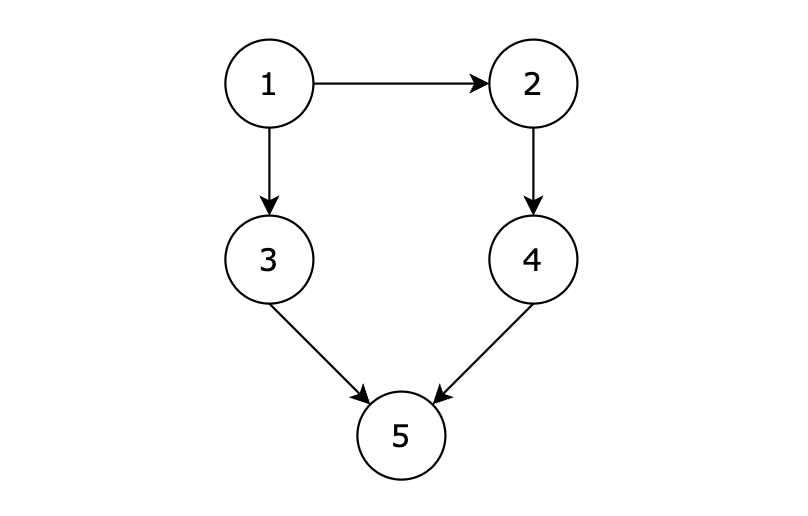
用例解释：

有五个节点，其中的从 1 到达 5 的路径有两个，分别是 1 -> 3 -> 5 和 1 -> 2 -> 4 -> 5。

因为拥有多条路径，所以输出结果为：

1 3 5
1 2 4 5

或

1 2 4 5
1 3 5
都算正确。

数据范围：

• 图中不存在自环
• 图中不存在平行边
• 1 <= N <= 100
• 1 <= M <= 500

1.邻接矩阵法

#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> result;
vector<int> path;

void dfs(vector<vector<int>>&graph,int x,int n)
{
    if(x==n)
    {
        result.push_back(path);
        return;
    }
    for(int i=1;i<=n;i++)
    {
        if(graph[x][i]==1)
        {
            path.push_back(i);
            dfs(graph,i,n);
            path.pop_back();
        }
    }
}

int main()
{
    int n,m,s,t;
    cin>>n>>m;
    vector<vector<int>> graph(n+1,vector<int>(n+1,0));
    while(m--)
    {
        cin>>s>>t;
        graph[s][t]=1;
    }
    path.push_back(1);
    dfs(graph,1,n);
    if(result.size()==0) cout<<-1<<endl;
    for(int i=0;i<result.size();i++)
    {
        for(int j=0;j<result[i].size()-1;j++)
        {
            cout<<result[i][j]<<" ";
        }
        cout<<result[i][result[i].size()-1]<<endl;
    }
    return 0;
}

2.邻接表法

#include <iostream>
#include <vector>
#include <list>
using namespace std;

vector<vector<int>> result;
vector<int> path;

void dfs(vector<list<int>> &graph,int x,int n)
{
    if(x==n)
    {
        result.push_back(path);
        return;
    }
    for(int i:graph[x])
    {
        path.push_back(i);
        dfs(graph,i,n);
        path.pop_back();
    }
}
int main()
{
    int n,m,s,t;
    cin>>n>>m;

    vector<list<int>> graph(n+1);
    while(m--)
    {
        cin>>s>>t;
        graph[s].push_back(t);
    }

    path.push_back(1);
    dfs(graph,1,n);

    if(result.size()==0) cout<<-1<<endl;
    for(int i=0;i<result.size();i++)
    {
        for(int j=0;j<result[i].size()-1;j++)
        {
            cout<<result[i][j]<<" ";
        }
        cout<<result[i][result[i].size()-1]<<endl;
    }
    return 0;
}