xtu oj 神经网络

news2024/12/23 9:05:12

回顾

Dedicated to you.

A+B III
问题 H: 三角数
问题 G: 3个数
等式数组下标查询，降低时间复杂度
1405 问题 E: 世界杯
xtu 数码串

题目

某神经网络模型是如下
1.一共有m层，每层都有几个神经元，从上到下编号为1到n。
2.第 i 层的神经元只有第 i + 1 层的神经元单向联系，第 m 层没有与其他神经元联系。
3.对于第 i 层的第 j 个神经元，将于第 i + 1 层的第 k 个神经元联系，且对于不同的 j ，对应的 k 也不同。
4.所有层之间的联系对应关系是一样的。
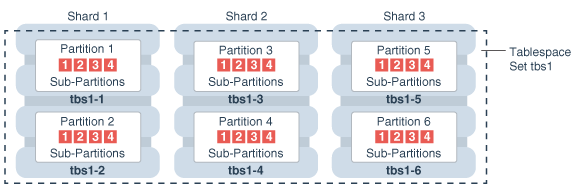
5.对于联系的神经元对 < j,k > ,如果 k>1 ,将影响 k 和 k-1 号神经元:否则只影响第 1 号神经元比如如下图所示。一共 3 层，每层 4 个神经元，前一层的神经元依次影响后一层的神经元序号为 (3,2,4,1) 。
在这里插入图片描述

思路

对笔者来说这题还是比较难的。主要是前面一个神经元映射到后面那层的神经元，然后还要往后继续映射，我该怎么保存哪个神经元被映射了呢？下面为了描述方便，笔者把神经元简称为元素。
题目描述的意思是，映射规则每一层都是一样的，这里的层和日常生活中的层不太一样，这里是竖着的层，可能需要我们在思维上绕一下。只要映射到的元素不是所在层的最上面的元素，那么该元素的上面一个元素也会被映射到，或者说被影响到。这里说的映射就是题干里面描述的影响。也就是说，有直接映射和间接映射两种情况。
我们需要把前面被直接映射和被间接映射到的元素标记出来，因为只有被映射的元素才能影响后面的元素。（请仔细思考这句话，思考要怎么实现这个逻辑，这是解题的关键）
还有一个，线性代数里面的知识点，可能也不算吧，可能算基本常识，反正笔者觉得比较绕，就是这一段话。

我们可以用一个矩阵来表示这个影响关系，如果第 1 层的第 j 个神经元影响第 3 层的第 i 个神经元，则 $a_{ij}=1$ ;否则 $a_{ij}=0$

上面的话的意思是，一个二维矩阵，我们是一列一列来看的，就是和我们的日常习惯一行一行看不太一样，是一列一列看这个元素，一列看下来，数字为 $1$ 就表示该行号对应的元素被列号表示的元素影响了，比如说 $a_{12}$ 表示最后一层的第二个元素被第一层的第一个元素影响了。该题需要输出的是，第一层的元素和最后一层元素之间的映射关系，或者说影响矩阵。顺带说一句，数字和数字之间不能输出空格（血泪教训）
也就是说，行号表示的是一层被影响的元素，列号表示的是第一层的元素，请记住这一点再看代码。
假设有三层，需要映射两次，那么有 m 层，需要映射 m-1 次。第一层的每一个元素都需要映射 m-1 次，从第一层的一个元素经过第一次映射到第二层之后，进行第二次映射的时候，我们不知道被影响的元素是哪些，第一次映射的前提是我们知道映射的自变量是什么，但是第二次映射的时候我们不知道映射的自变量是什么（可以理解为手电筒发出光源，不知道手电筒在哪里）。所以需要对被影响的元素做上标记，标记的内容是第多少次映射（具体到我的这份代码里面就是 j ，1~m-1 那个循环里面的 j）。
二维数组 ans 表示的就是答案数组，请参考 6. 写的，行号表示被影响的元素，列号表示自变量（发出映射的源头），有点像一个这样的过程：从下标到一个数值，把这个数值作为下标，再得到一个数值，不断循环，让这个过程转起来
flag 是标记数组，或者称之为中间临时变量也可以，因为它的作用就是在中间的时候判断一下，前面这个元素在上一次映射里面 ( j-1 ) 有没有被映射到，假设被映射到了，在当前这次映射里面（第 j 次映射）就可以作为映射的自变量（源头）

if(ans[i][j]==m-1){
   	ans[i][j]=1;
}else{
   ans[i][j]=0;
}

这里判断和 m-1 是否相等的意思就是，判断最后一层的第 i 个元素在最后一次映射（第 m-1 次）有没有被映射到，这个映射的根源是第一层的第 j 个元素，被映射到了，说明就是被影响了。

c 语言代码

#include<stdio.h>
#define N 110

int ans[N][N];
int a[N];
int flag[N];

int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		int n,m;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++){
			scanf("%d",&a[i]);
		}
		
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				flag[j]=0;
			}
			
			for(int j=1;j<=m-1;j++){
				for(int k=1;k<=n;k++){
					if(j==1){
						ans[a[i]][i]=j;
						if(a[i]!=1){
							ans[a[i]-1][i]=j;
						}
					}else if(flag[k]==j-1){
						ans[a[k]][i]=j;
						if(a[k]!=1){
							ans[a[k]-1][i]=j;
						}
					}
				}
				
				for(int k=1;k<=n;k++){
					flag[k]=ans[k][i];
				}
			}
		}
		
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(ans[i][j]==m-1){
					ans[i][j]=1;
				}else{
					ans[i][j]=0;
				}
				printf("%d",ans[i][j]);
			}
			puts("");
		}
		puts("");
		
		for(int i=0;i<N;i++){
			for(int j=0;j<N;j++){
				ans[i][j]=0;
			}
		}
	}
	
	return 0;
}