目录
- 树的基本概念
- 树的定义
- 树的特点
- 树的相关术语
- 度
- 层数
- 高度
- 路径
- 二叉树
- 定义
- 特点
- 定理
- 满二叉树
- 定义
- 特点
- 完全二叉树
- 定义
- 特点
- 二叉树的存储结构
- 顺序存储
- 结点结构
- 优点缺点
- 链式存储
- 结点结构
- 三叉链表表示法
- 算法
- 搜索结点的父结点
- 搜索符合数据域条件的结点
- 删除给定结点及其左右子树
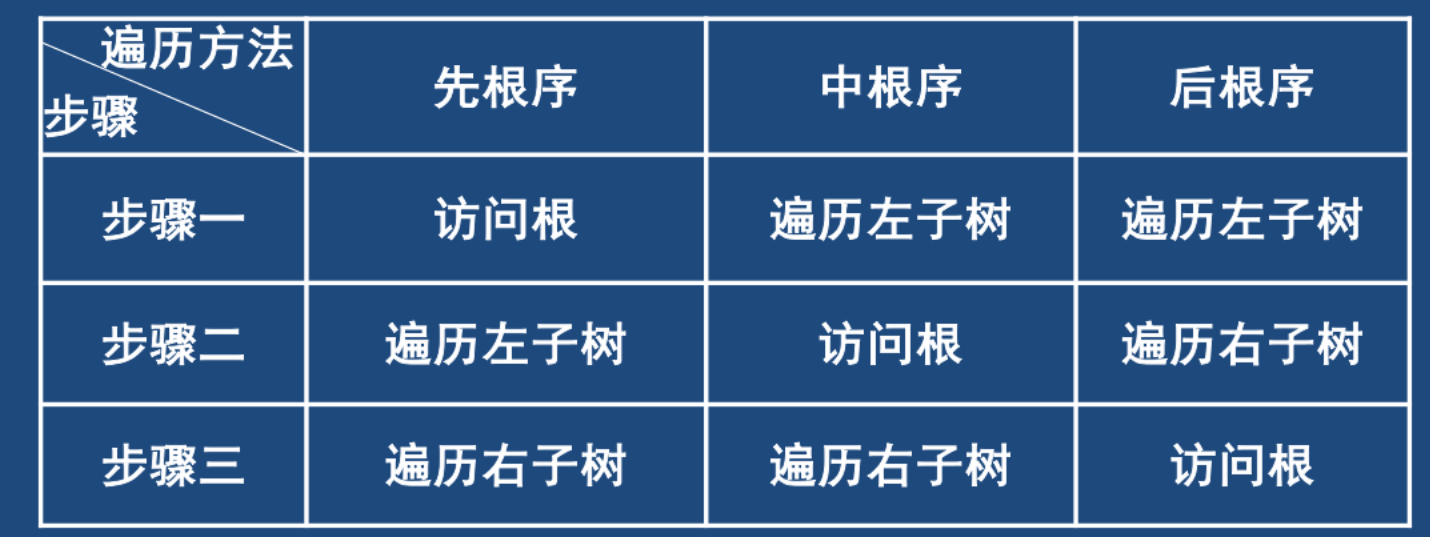
- 二叉树遍历
- 先根遍历
树的基本概念
- 树结构在客观世界中大量存在,例如家谱、行政组织机构都可用树结构形象地表示
- 树在计算机领域中也有着广泛的应用,例如在编译程序中,用树来表示源程序的语法结构;在数据库系统中,可用树来组织信息;在分析算法的行为时,可用树来描述其执行过程


树的定义
-
(递归定义)定义:一个树(或树形)就是一个有限非空的结点集合T,其中:
-
有一个特别标出的被称为该树(或树形)之根root(T)的结点
-
其余结点 (根除外)被分成m≥0个不相交的集合T1,T2,...,Tm,且T1,T2,...,Tm又都是树(或树形)。树(或树形)T1,T2,...,Tm被称作root(T)的子树(或子树形)
-
-
(非递归定义)定义:树是包含n(n≥1)个结点且满足如下条件的有限集合
-
存在一个唯一的结点v0,它没有前驱结点,称为树的根(或根结点)
-
任何非根结点都有且仅有前驱节点,称为该节点的父结点
-
任何结点都可能有多个(≤n-1)后继结点,称之为该结点的子结点;若某结点没有后继结点,则称之为叶结点
-
任一非根结点vk都有且仅有一条从v0到该结点序列(或路径)v0 → v1 → ...→ vk,其中vi是vi-1(1≤i≤k)的子结点
-
-
其他定义:t是有一个有限元素的集合,其中一个元素为根,余下的元素(如果有的话)组成t的子树(subtree)。层次中最高层的元素为根,其下一级的元素是余下元素所构成的子树的根
例:
下图为一颗由根结点A发出的树,其中
- A有三个子结点B、C和D(换句话说A是B、C和D的父结点)
- B有一个子结点E
- E有一个子结点F
- C有两个子结点G和H;D有一个子结点I;F、G、H、I是叶子结点,因为它们没有子结点

- 若断掉一个结点与其父结点的连接,把该结点和它的子孙们单独拿出,就是一棵以该结点为根结点的树,称之为“子树”。

树的特点

- 树中任一结点都可以有零个或多个直接后继(即子结点),但至多只能有一个直接前驱(即父结点)
- 树中只有根结点无前驱,它是始结点;叶结点无后继,它们是终结点
- 树中某些结点之间具有父子关系或者祖先、子孙关系,祖先、子孙关系是对父子关系的扩展,一些结点之间,如兄弟结点(同一个父亲的诸子结点被称为兄弟结点)之间就没有这种关系
- 有一个树根
- 没有分枝相交
- 树有层次
树的相关术语
度
- 结点的度
- 一个结点的子结点的数目,称为该结点的度或者次数。一棵树的度为maxi=1,...,nD(i),其中n为树中结点总数,i指树中的第i个结点,D(i)表示结点i的度
- 树的度
- 树中各结点的最大值
- 示例:
- B有一个子结点E,度为1;A有三个子结点B、C和D(换言之,A是B、C和D的父结
点),度为3,这棵树的度也为3
- B有一个子结点E,度为1;A有三个子结点B、C和D(换言之,A是B、C和D的父结

层数
- 结点的层数:树形T中结点的层数递归定义如下
- root(T)层数为0
- 其余结点的层数为其前驱结点的层数加一

高度
-
树的高度为maxi=1,...,nNL(i),其中n为树中结点总数,i指数中第i个结点,NL(i)之值为结点i的层数
-
树的高度是指树中结点的最大层数
路径
- 树形中结点间的连线被称为边。若树形T中存在结点序列vm→vm+1→...→vm+k,1≤k≤T的最大层数满足vi+1是vi;(m≤i≤m+k-1)的子结点,则称此结点序列为vm到vm+k的路径,该路径所经历的边数k被称为路度径长
- 子孙结点、祖宗结点
- 一棵树中若存在结点vm到vn的路径,则称vn为vm的子孙结点,vm为vn的祖宗结点
- 一个结点到它某个子孙结点有且仅有条路径
二叉树
定义
二叉树(形)是结点的有限集合,它或者是空集,或者由一个根及两个不相交的,称为这个根的左、右子树形的二叉树组成
特点
- 二叉树每个结点最多有两个子结点
- 二叉树的子树有左右之分
- 树与二叉树的主要区别
- 二叉树每个结点最多有两个子结点,树则没有限制
- 二叉树中结点的子树分成左子树和右子树,即使某结点只有一颗子树,也要指明该子树是左子树还是右子树,就是说二叉树是有序的
- 含有三个结点的不同二叉树

定理
- 二叉树中层数为i的结点至多有2^i个,i≥0
- 证明:
- 当i=0时,仅有一个根结点,其层数为0,因此i=0时引理成立
- 假定当i=j(j≥0)时,引理成立,即第j层上至多有2个结点
- 对于二叉树的任意结点,其子结点个数最大为2,故第j+1层上至多有2*
2^j=2^(j+1)个结点,因此当i=j+1时,引理成立 - 由数学归纳法可知,对于所有的i≥0,均有“第i层上至多有2^i个结点,证毕。
- 证明:
- 高度为k(k≥0)的二叉树中至少有k+1个结点,含有k(k≥1)个结点的二叉树高度至多为k-1
例:

- 高度为k的二叉树中至多有2^(k+1)-1(k≧0)个结点
- 证明
- 第0层上至多有2^0个结点
- 第1层上至多有2^1个结点
- 第2层上至多有2^2个结点
- ......
- 第k层上至多有2^k个结点
- 因此,高度为k的二叉树中至多有2^0+2^1+...+2^k=2^(k+1)-1个结点
- 证明
- 设T是由m个结点构成的二叉树,其中度为2的结点个数为n2,度为0(叶结点)的个数为n0,则n0=n2+1
- 证明:
- 若度为1的结点个数为n1,总结点个数为n,则n=n0+n1+n2
- 所有度为2结点的子结点总数的结点总数为2*n2,同理度为1结点的子结点总数为1*n1,度为0结点的子结点总数为0,则n=2*n2+n1+1(加上树的根)
- n0+n1+n2 = 2*n2+n1+1
- n0=n2+1
- 证明:
满二叉树
定义
一棵非空高度为k(k≥0)的满二叉树,是有2^(k+1)-1个结点的二叉树

特点
- 高度为k(非空)二叉树至多有2^(k+1)-1个结点
- 满二叉树的特点是:
- 叶结点都在第k层上
- 每个分支结点都有两个子结点
- 叶结点的个数等于非叶结点个数加1
- 除叶结点外,其他结点的度均为2
完全二叉树
定义
- 一棵有n个结点、高为k的二叉树T,一棵高为k的满二叉树T*,用正整数按层次顺序分别编号T和T*的所有结点,如果T之所有结点恰好对应于T*的前n个结点,则称T为完全二叉树
- 层次顺序:按从上至下,即从第0至第k层,每层由左到右的次序

特点
-
具有n个结点高度为k的完全二叉树具有如下特点
- 树中只有最下面两层结点的度可以小于2
- 树中最下面一层的结点都集中在该层最左边的若干位置上(满二叉树意义上)
- 树中叶结点只能在层数最大的两层上出现,即存在一个非负整数k使得树中每个叶结点或在第k层或第k+1层上
- 对树中所有结点,按层次顺序,用自然数从1开始编号,仅仅编号最大的非叶结点可以没有右孩子,其余非叶结点都有两个孩子结点
- 若将一棵具有n个结点的完全二叉树按层次次序从1开始编号,则对编号为i(1≤i≤n)的结点有
- 若i≠1,则编号为i的结点的父节点的编号为i/2
- 若2i≤n,则编号为i的结点的左孩子的编号为2i,否则i无左孩子
- 若2i+1≤n,则编号为i的结点的右孩子的编号为2i+1,否则i无右孩子
- 仅仅编号最大的非叶结点可无右孩子,但必须有左孩子,其余非叶结点都有两个孩子结点
- 用归纳法证明
- 若i=1,如果n≥2,则左孩子的编号显然为2
- 假定对所有j(1≤j≤i,2i≤n),有j的左孩子编号为2j
- 那么对于结点i+1,证明其左孩子编号为2(i+1)
- 如果2(i+1)≤n,则由层次次序得知,i+1的左孩子之前的两个结点就是i的左孩子和右孩子,因为i的左孩子编号为2i(归纳假设),故i的右孩子编号为2i+1,从而i+1的左孩子编号为2i+2=2(i+1)
- 证毕
- 具有n个结点的完全二叉树的高度是
- 设二叉树高度为k,由定义知,完全二叉树的结点个数介于高度为k-1和高度为k的满二叉树的结点数之间,即有:2^k-1<n≤2^(k+1)-1
- 从而有2^k≤n<2^(k+1),即k≤log2n<k+1,因为k为整数,故有k=log2n
二叉树的存储结构
要存储一棵二叉树,需存储其所有结点的数据信息,以及其左、右孩子的地址
通常有两种存储方式:
- 顺序存储
- 链接存储
顺序存储
指将二叉树的所有结点按照层次顺序存放在一块地址连续的存储空间中,同时要反映二叉树中的结点间的逻辑顺序
结点结构
- 完全二叉树顺序存储方式:按照层次顺序
- 结点编号恰好反映了结点间的逻辑关系
- 示例:一维数组A存储二叉树
- A[1]存储二叉树的根结点,A[i]存储二叉树中编号为i的结点,并且结点A[i]的左孩子(若存在)存放在A[2i]处,而A[i]的右孩子(若存在)存放在A[2i+1]处


优点缺点
- 顺序存储的完全二叉树:
- 优点:简单、节省空间
- 只存储结点信息域、未存储其左孩子和右孩子。通过计算可找到它的左孩子、右孩子和父节点,寻找子孙结点和祖先结点也非常方便
- 顺序存储存储非完全二叉树
- 编号不能与结点一一对应
- 解决方案:先加入若干虚结点将其转化成一棵“完全二叉树”,然后再将对原来的结点和虚结点统一编号,最后完成顺序存储。但这增加了用于存储虚结点的空间
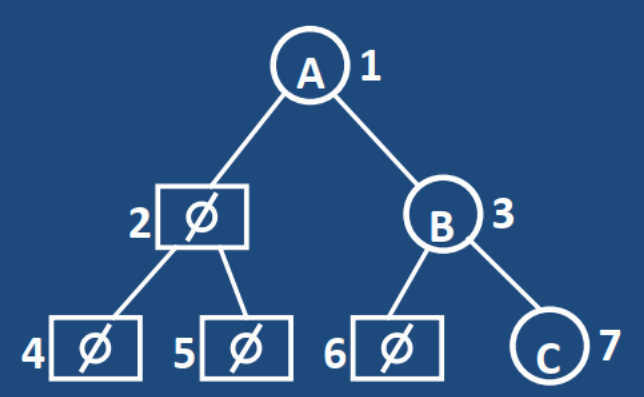
链式存储
二叉树各结点随机存放在内存空间中,结点之间的关系用指针标识
- 有一个指向根节点的指针,称为根指针root,二叉树通过根指针来访问,二叉树为空,即root = NULL
- 若某结点左孩子或右孩子不存在,则对应指针为NULL
- 包含n个结点的二叉树用链式存储表示,需要2n个指针域,其中n-1个用来表示结点的左右孩子,其余n+1个指针域为空
结点结构
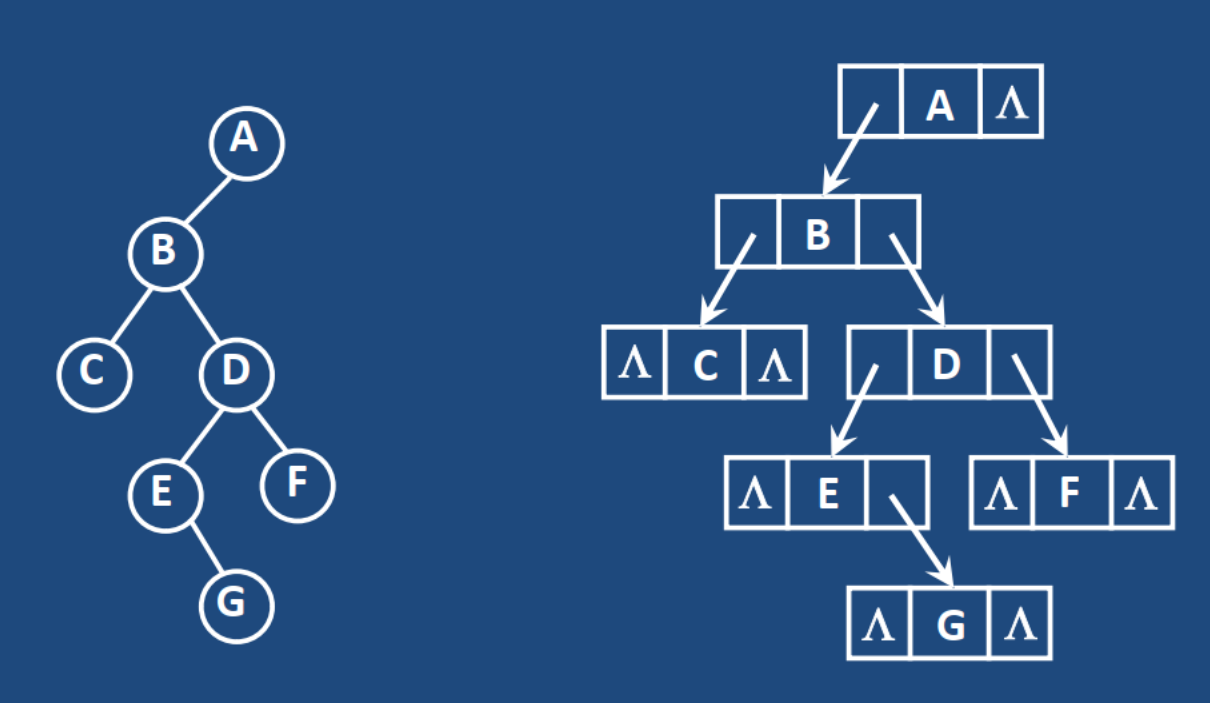
二叉树结点应包含三个域:数据域data、指针域left(左指针)和指针域right(右指针),其中左、右指针分别指向该结点的左、右子树的根结点

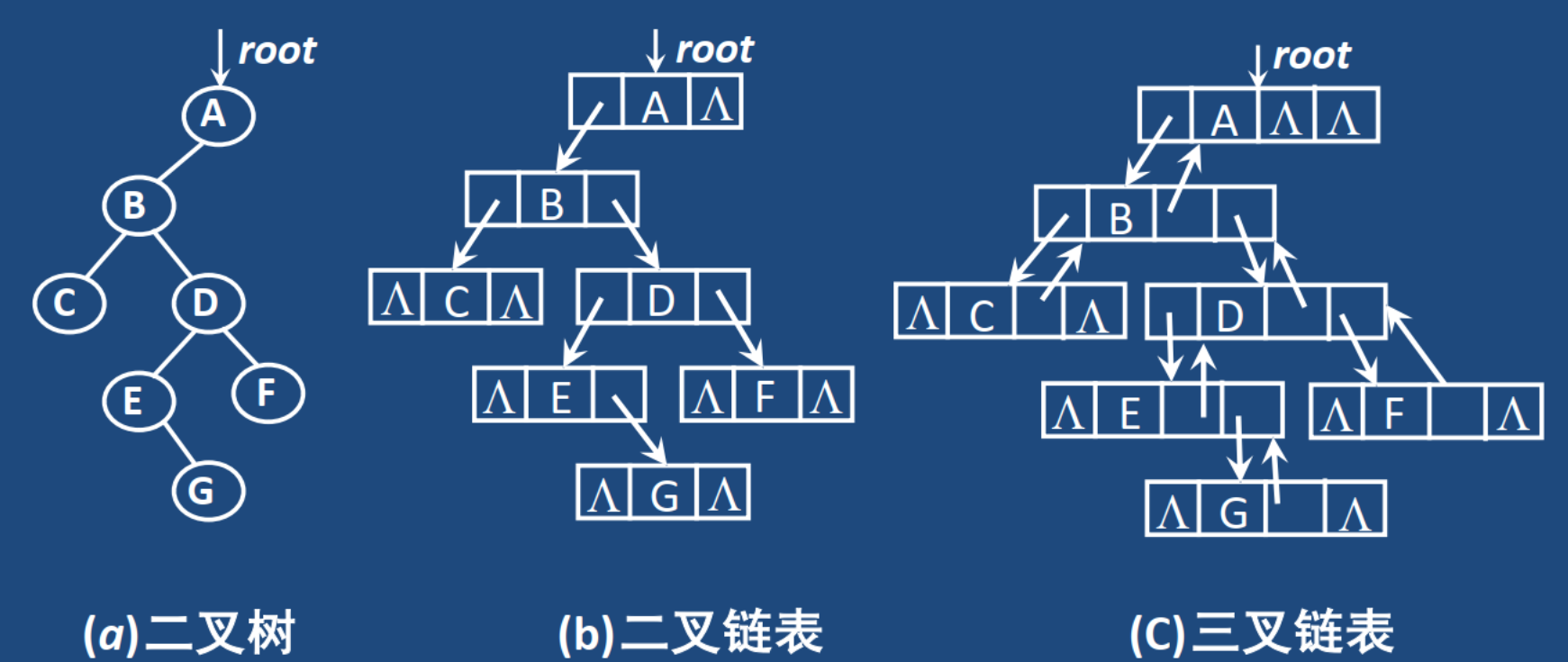
三叉链表表示法
结点包括三个指针域,parent域中的指针指向其父结点

算法
搜索结点的父结点
#include <iostream>
using namespace std;
class Tree
{
protected:
int data;
Tree *left;
Tree *right;
public:
Tree(int d) // 构造函数,创建树的节点
{
data = d;
left = NULL;
right = NULL;
}
Tree* Left() // 返回左子树
{
return left;
}
Tree* Right() // 返回右子树
{
return right;
}
int Data() // 返回节点数据
{
return data;
}
void setLeft(Tree *l) // 设置左子树
{
left = l;
}
void setRight(Tree *r) // 设置右子树
{
right = r;
}
};
// Father 函数用于查找某个节点的父节点
void Father(Tree* t, Tree* p, Tree*& q) // 通过引用传递 q
{
if (t == NULL || t == p)
{
q = NULL;
return;
}
if (t->Left() == p || t->Right() == p) // 找到父节点
{
q = t;
return;
}
Father(t->Left(), p, q); // 递归搜索左子树
if (q == NULL)
{
Father(t->Right(), p, q); // 递归搜索右子树
}
return;
}
int main()
{
// 创建树节点
Tree *t = new Tree(1);
t->setLeft(new Tree(2));
t->setRight(new Tree(3));
t->Left()->setLeft(new Tree(4));
t->Left()->setRight(new Tree(5));
t->Right()->setLeft(new Tree(6));
t->Right()->setRight(new Tree(7));
// 查找节点 t->Left()->Left()(也就是节点 4)的父节点
Tree *p = t->Left()->Left();
Tree *q = NULL;
Father(t, p, q);
// 输出父节点的数据,如果父节点存在
if (q != NULL)
{
cout << q->Data() << endl;
}
else
{
cout << "NULL" << endl;
}
return 0;
}
搜索符合数据域条件的结点
// Find 函数用于查找某个节点
Tree* Find(Tree* t,int data,Tree*& q) // 通过引用传递 q
{
if(t==NULL)
{
q=NULL;
return q;
}
if(t->Data()==data)
{
q=t;
return q;
}
q=Find(t->Left(),data,q);
if(q==NULL)
{
q=Find(t->Right(),data,q);
}
return q;
}
int main()
{
// 创建树节点
Tree *t = new Tree(1);
t->setLeft(new Tree(2));
t->setRight(new Tree(3));
t->Left()->setLeft(new Tree(4));
t->Left()->setRight(new Tree(5));
t->Right()->setLeft(new Tree(6));
t->Right()->setRight(new Tree(7));
// 查找节点 t->Left()->Left()(也就是节点 4)值为4
Tree *p = t->Left()->Left();
Tree *q = NULL;
q = Find(t,p->Data(),q);
// 输出找到结点的值
if (q != NULL)
{
cout << q->Data() << endl;
}
else
{
cout << "NULL" << endl;
}
return 0;
}删除给定结点及其左右子树
// 递归删除给定节点及其左右子树
void Del(Tree* root)
{
if (root == NULL)
return;
// 递归删除左子树和右子树
Del(root->Left());
Del(root->Right());
delete root;
}
// 查找并删除树中的某个节点及其左右子树
void DeleteNode(Tree* root, Tree* target)
{
if (target == NULL) return;
if (target == root)
{
Del(root);
root = NULL;
return;
}
Tree* parent = NULL;
// 查找目标节点的父节点
Father(root, target, parent);
if (parent->Left() == target) parent->setLeft(NULL);
if (parent->Right() == target) parent->setRight(NULL);
Del(target);
target = NULL;
return;
}
int main()
{
// 创建二叉树
Tree* t = new Tree(10);
t->setLeft(new Tree(5));
t->setRight(new Tree(15));
t->Left()->setLeft(new Tree(3));
t->Left()->setRight(new Tree(7));
t->Right()->setLeft(new Tree(12));
t->Right()->setRight(new Tree(18));
// 目标节点为 t->Left()(节点 5),我们要删除它及其左右子树
Tree* target = t->Left();
DeleteNode(t, target);
return 0;
}二叉树遍历
二叉树为空则什么都不做;否则遍历分三步进行
例子:
- 先根遍历得到的结点序列:x+AB+x-CDEF
- 中根遍历得到的结点序列:A+BxC-DxE+F
- 后根遍历得到的结点序列:AB+CD-ExF+X
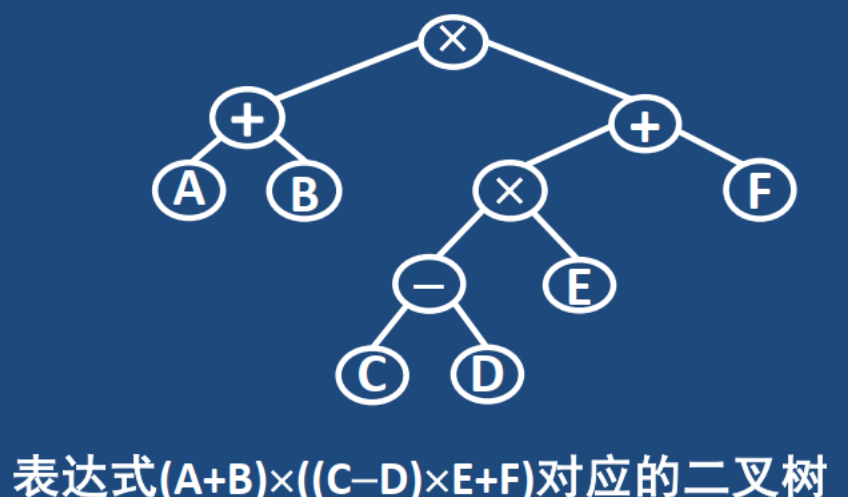
- 对于给定的一棵二叉树,可给出在先根序、中根序和后根序下的唯一结点排列
- 三种遍历序列的叶结点间的相对次序是相同的,叶结点都是按着从左到右的次序排列,区别仅在于非叶结点间的次序以及非叶结点和叶结点间的次序有所不同
先根遍历
- 若二叉树为空,则空操作
- 否则
- 访问根节点
- 先根遍历左子树
- 先根遍历右子树
Preorder(t)
{
if t !=NULL;
{
print(data(t));
Perorder(Left(t));
Perorder(Right(t));
}
}
其他遍历方法即是将 print(data(t));Perorder(Left(t));Perorder(Right(t));三者顺序调换