摘要
本研究基于MATLAB仿真平台,探讨了储能系统在电力系统中辅助调峰的容量需求问题。通过对风电、微型燃气机等分布式能源的实际出力曲线与理论输出进行比较分析,我们探讨了在不同负荷条件下储能系统的调峰能力。实验结果表明,储能系统的合理配置可以有效平滑电力波动,减少电力系统的调峰压力。
理论
电力系统的调峰需求与负荷特性和可再生能源的输出波动性密切相关。储能系统可以通过在负荷低谷时充电、高峰时放电,平衡系统的供需差异。本文采用的调峰模型包括风电出力的理论值与实际值对比,以及储能系统在不同时间段内的充放电行为分析。理论基础包括功率平衡方程和储能系统的功率变化率公式,具体为:
![]()
实验结果
通过MATLAB进行仿真,分别得到了风电出力的理论值和实际值、储能系统的充放电功率随时间的变化,以及微型燃气机和风电联合运行下的电力平衡图。以下为关键实验图表分析:
-
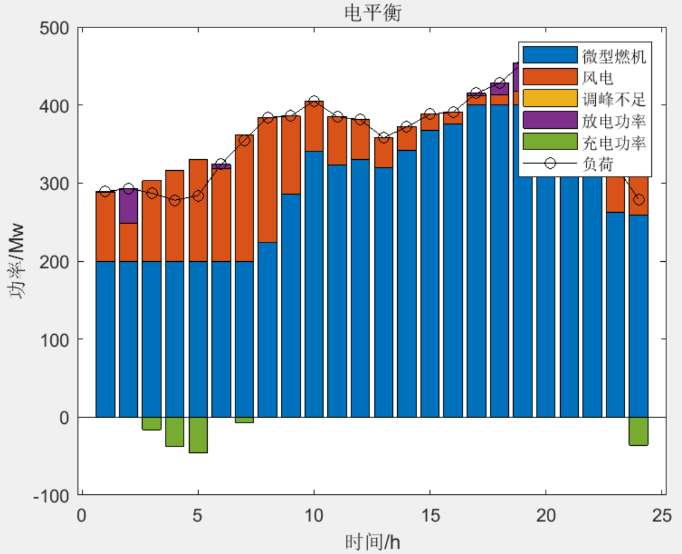
图1:功率平衡分析,包括风电、微型燃气机和储能系统的功率变化。
-
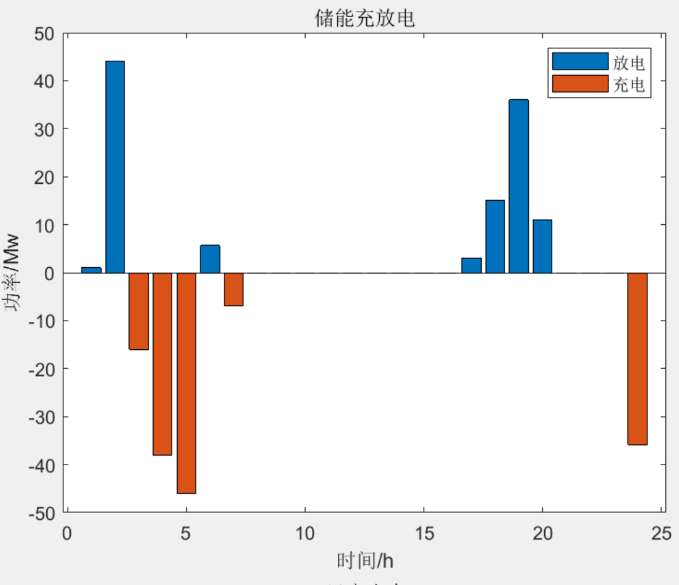
图2:储能系统在不同时间段的充放电行为。
-
图3:风电的理论出力与实际出力比较,验证了储能系统调峰的必要性。

部分代码
% 风电出力仿真
time = 0:1:24; % 时间区间
P_theoretical = 160 * sin(pi * time / 12); % 理论风电功率
P_actual = P_theoretical - randn(1, 25) * 10; % 实际风电功率
% 绘制理论出力和实际出力对比图
figure;
plot(time, P_theoretical, 'b-o', 'DisplayName', '理论出力');
hold on;
plot(time, P_actual, 'r-*', 'DisplayName', '实际出力');
xlabel('时间/h');
ylabel('功率/Mw');
title('风电出力');
legend;
% 储能系统充放电仿真
P_storage_charge = zeros(1, 25); % 初始化充电功率
P_storage_discharge = zeros(1, 25); % 初始化放电功率
% 设定充放电时间和功率
P_storage_charge(5:7) = -40; % 在5-7时充电
P_storage_discharge(19:21) = 40; % 在19-21时放电
% 绘制储能系统充放电功率图
figure;
bar(time, [P_storage_discharge', P_storage_charge'], 'stacked');
xlabel('时间/h');
ylabel('功率/Mw');
title('储能充放电');
legend('放电', '充电');
参考文献
❝
Banos, R., Manzano-Agugliaro, F., Montoya, F. G., Gil, C., Alcayde, A., & Gómez, J. (2011). Optimization methods applied to renewable and sustainable energy: A review. Renewable and Sustainable Energy Reviews, 15(4), 1753-1766.
Zhang, H., Wang, C., Xu, G., Zhang, X., & Tan, Z. (2019). A review of the applications of energy storage systems in renewable energy integration. Renewable Energy, 139, 599-617.
Li, Y., & Dai, H. (2020). Capacity optimization of energy storage system considering power system peak shaving demand. Applied Energy, 262, 114550.