学习文档:代码随想录 (programmercarl.com)
Leetcode 669. 修剪二叉搜索树
题目描述
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
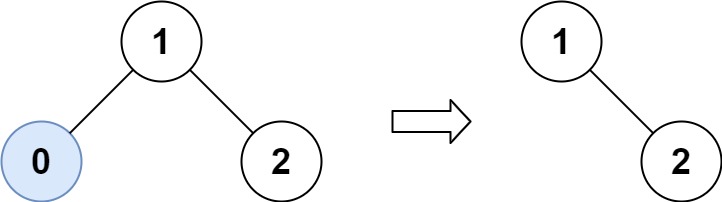
输入:root = [1,0,2], low = 1, high = 2 输出:[1,null,2]
解题思路
直接想法就是:递归处理,然后遇到 root->val < low || root->val > high 的时候直接return NULL。但是要考虑到特殊情况:要考虑到0的右子树,可以将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点0从二叉树中移除),因为是二叉搜索树,节点0小于low,那么只需要将右子树赋给节点3的左孩子即可。

完整代码
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr ) return nullptr;
// 如果root的元素小于low的数值,那么应该递归右子树,并返回右子树符合条件的头结点
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
return right;
}
// 如果root的元素大于high的数值,那么应该递归左子树,并返回左子树符合条件的头结点
if (root->val > high) {
TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
return left;
}
root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
return root;
}
};Leetcode 108. 将有序数组转换为二叉搜索树
题目描述
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵
平衡
二叉搜索树。
示例 1:
输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
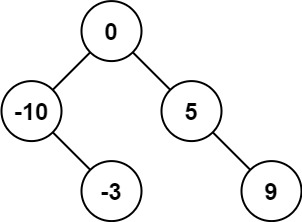
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
解题思路
在二叉树:构造二叉树登场! (opens new window)和代码随想录 (programmercarl.com)中其实已经讲过了,如果根据数组构造一棵二叉树。
本质就是寻找分割点,分割点作为当前节点,然后递归左区间和右区间。分割点就是数组中间位置的节点。如果数组长度为偶数,中间节点有两个,取哪一个?取哪一个都可以,只不过构成了不同的平衡二叉搜索树。
完整代码
class Solution {
private:
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left > right) return nullptr;
// 保证操作不会越界
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
TreeNode* root = traversal(nums, 0, nums.size() - 1);
return root;
}
};Leetcode 538.把二叉搜索树转换为累加树
题目描述
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。
示例 1:
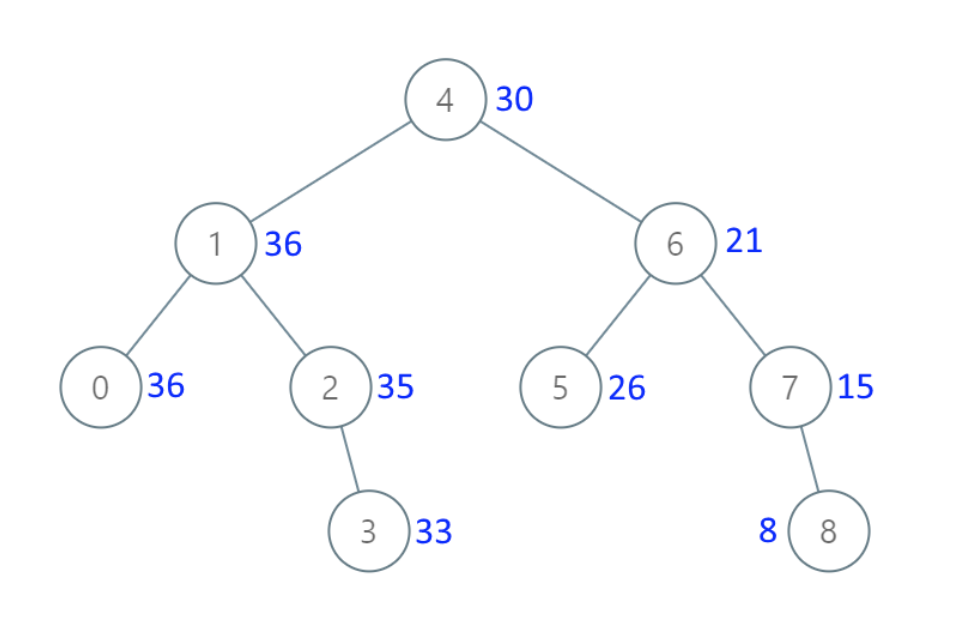
- 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
- 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
解题思路
将这个二叉搜索树 转化为有序数组来思考就是求这个数组从后到前的累加数组,[2, 5, 13]->[20, 18, 13],那么知道如何遍历这个二叉树,也就迎刃而解了,从树中可以看出累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,然后顺序累加就可以了。
需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加
完整代码
class Solution {
private:
int pre = 0; // 记录前一个节点的数值
void traversal(TreeNode* cur) { // 右中左遍历
if (cur == NULL) return;
traversal(cur->right);
cur->val += pre;
pre = cur->val;
traversal(cur->left);
}
public:
TreeNode* convertBST(TreeNode* root) {
pre = 0;
traversal(root);
return root;
}
};


















