代码随想录 | Day28 | 回溯算法:组合&&组合总和III
关于这个章节,大家最好是对递归函数的理解要比较到位,听着b站视频课可能呢才舒服点,可以先去搜一搜关于递归函数的讲解,理解,再开始这个章节会比较好一些
我觉得回溯就是对传入递归函数的参数加加减减,加了的减掉,减了的加上
主要学习内容:
组合题目的模板
77.组合
[77. 组合 - 力扣(LeetCode)](https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/description/)
解法思路:
首先,把问题转换为树形结构,树的每一层的各个结点都是由本层逻辑的for循环产生的,树的深度是由我们所求集合的大小决定的。
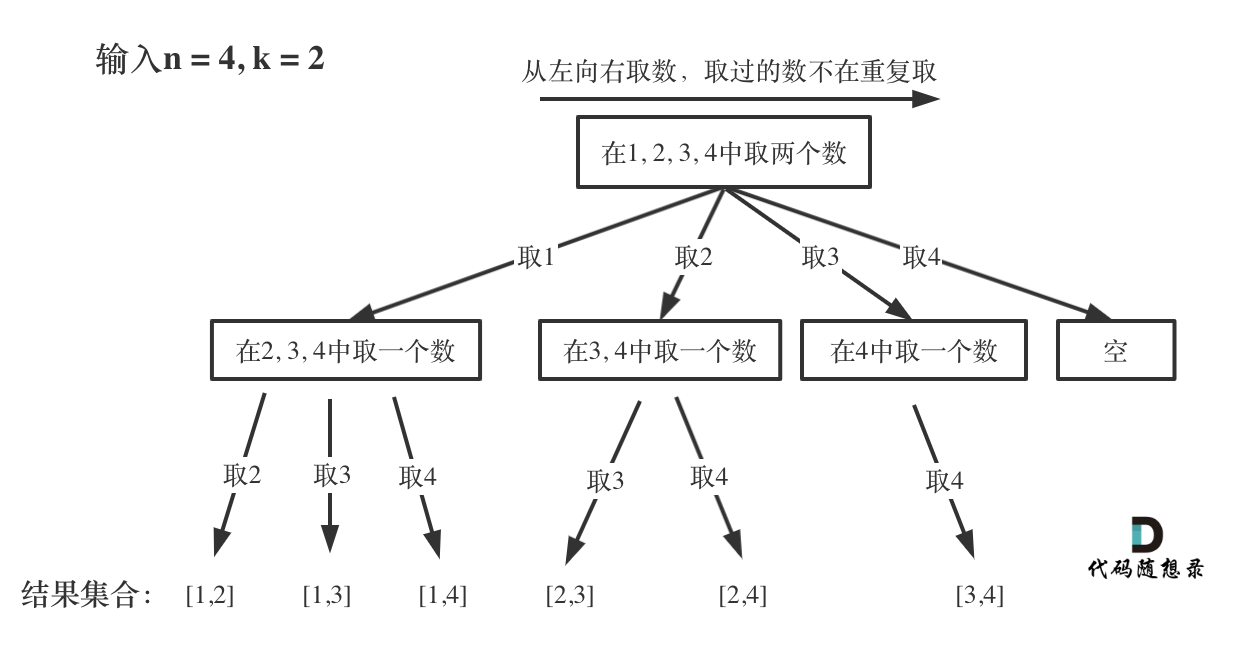
我们在第一层取出一个数字,第一层就是 1 ,2 ,3 ,4
第二层从剩余的集合中取出一个数字,那就是 [1,2] [1,3] [1,4] …
而我们集合大小为2,那么就只有这两层,树的深度也就这两层
而我们选完[1,2]怎么返回[1]的时候去选择[1,3]呢?
这时候就是回溯算法,回溯就是恢复你选择之前的状态,让你去选择另外一个,本质上是穷举的思想
1.函数参数和返回值
vector<vector<int>> res;
void backtracking(vector<int> path,int n,int k,int index)
res存放结果,path是当前已经收集的组合,n,k不必说,index表示我们已经选到哪个数字了,防止出现重复的组合
2.终止条件
我们当前收集的集合大小等于要求的大小就收集到最后的结果集中,然后返回,这也是能够控制树的深度只有两层的原因
if(path.size()==k)
{
res.push_back(path);
return;
}
3.本层代码逻辑
其实最难理解的就是for循环部分。
由于题目要求的是组合,我们只要防止重复,所以引入index,让index之前的已经选过的数不再出现,比如第一层选了2之后,index会让1和2不再出现,只会出现3,4,不会同时出现[1,2]和[2,1]这两个组合了
对for的理解可以脑补一下,举例比如选了1之后,本层的递归函数index是1
进入for循环,传入的先是2,在树的下一层,产生了[1,2]组合,大小满足2,结束递归返回上层,上层将2弹出,继续下一次循环,传入的就是3,产生了[1,3],以此类推
需要注意的是不要写成index+1,这个是错误的,会出现:在你选完第一层的数字后,不管你第一层选的数是多少,第二层都是从2开始的
错误案例
n=4,k=2

最后递归函数返回来以后,把咱压入的元素再弹出就好
for(int i=index;i<=n;i++)
{
path.push_back(i);
backtracking(path,n,k,i+1);//注意不是index+1
path.pop_back();//回溯,恢复现场
}
完整代码:
class Solution {
public:
vector<vector<int>> res;
void backtracking(vector<int> path,int n,int k,int index)
{
if(path.size()==k)
{
res.push_back(path);
return;
}
for(int i=index;i<=n;i++)
{
path.push_back(i);
backtracking(path,n,k,i+1);//注意不是index+1
path.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
vector<int> path;
backtracking(path,n,k,1);
return res;
}
};
优化
注意代码中i,就是for循环里选择的起始位置,可以循环的次数少一点。(大家可以看代码随想录中的)
for (int i = startIndex; i <= n; i++) {
接下来看一下优化过程如下:
- 已经选择的元素个数:path.size();
- 所需需要的元素个数为: k - path.size();
- 列表中剩余元素(n-i) >= 所需需要的元素个数(k - path.size())
- 在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
从2开始搜索都是合理的,可以是组合[2, 3, 4]。
所以优化之后的for循环是:
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
216.组合总和III
216. 组合总和 III - 力扣(LeetCode)
思路:
思路和上一题一模一样,就是上一题给定的n换成了9,然后多了一个加和的操作
加和的操作你可以等到有3个数以后再加起来进行比较,也可以在递归的过程中累加并且比较
1.函数返回值和参数
vector<vector<int>> res;
void backtracking(vector<int> path,int k,int sum,int n,int index)
res记录结果
path收集当前组合
k组合大小
n总和值
sum当前集合的总和
index从哪个数开始
2.终止条件
当前总和已经大于n了,没必要再递归了
如果大小等于k并且加起来等于n,收集结果,不等于n直接返回
if(sum>n)
return ;
if(path.size()==k)
{
if(sum==n)
res.push_back(path);
return;
}
3.本层逻辑
优化的思路一样的直接套用了
和上一题不一样的就是多加了一个总和值sum
让sum加上我们压入path的值i传入下层即可,下层函数会在终止条件进行比较。
for(int i=index;i<=9-(k-path.size())+1;i++)
{
path.push_back(i);
backtracking(path,k,sum+i,n,i+1);//也可以写成 递归函数前写sum+=i,递归函数后写sum-=i,也可以写在递归函数参数中,比如我这样的
path.pop_back();//回溯过程
}
完整代码:
class Solution {
public:
vector<vector<int>> res;
void backtracking(vector<int> path,int k,int sum,int n,int index)
{
if(sum>n)
return ;
if(path.size()==k)
{
if(sum==n)
res.push_back(path);
return;
}
for(int i=index;i<=9-(k-path.size())+1;i++)
{
path.push_back(i);
backtracking(path,k,sum+i,n,i+1);
path.pop_back();
}
}
vector<vector<int>> combinationSum3(int k, int n) {
vector<int> path;
backtracking(path,k,0,n,1);
return res;
}
};