算法题总结（七）—

1、栈常用操作

（1）栈定义
Stack<Integer> stack = new Stack<Integer>();

（2）栈操作
.栈是否为空
isEmpty();
.查询栈顶元素，不改变栈
peek();
.弹出栈顶元素，改变栈
pop();
.压入栈顶
push();
.栈中元素的个数
size();

2、队列常用操作

Queue queue = new LinkedList();

Queue 单端队列：

Deque双端队列：

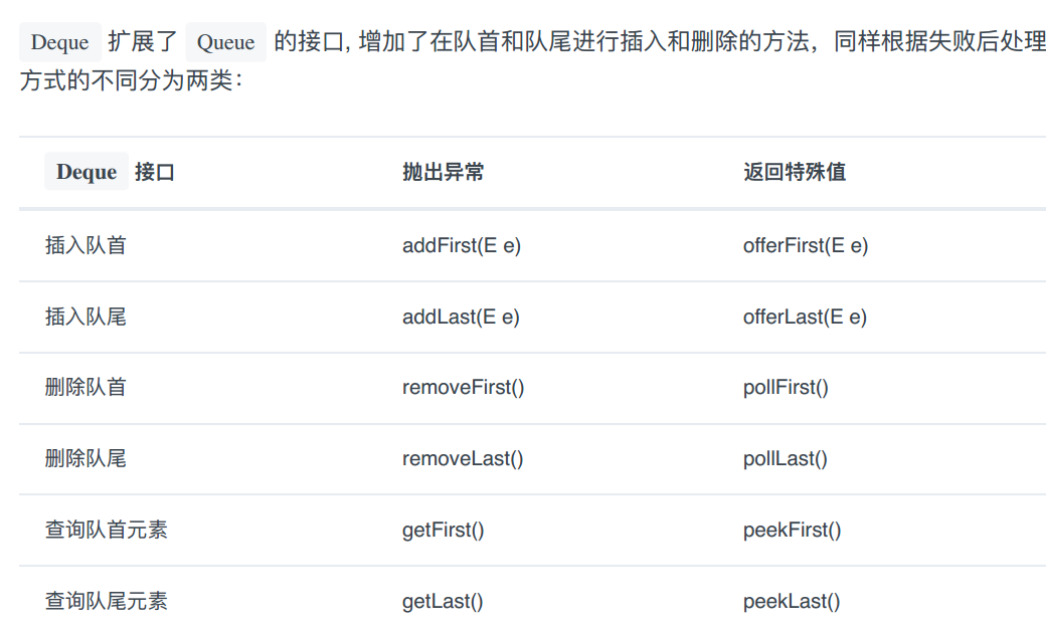
3、用栈实现队列

用两个栈来模拟队列，一个负责进栈，一个负责出栈，当出队的时候，从输出栈里出，如果是空的，把入栈全部放入输出栈中。

、class MyQueue {
    Stack<Integer> StackIn;
    Stack<Integer> StackOut;

    public MyQueue() {
        StackIn =new Stack<>(); //负责进栈
        StackOut =new Stack<>(); //负责出栈
    }

    public void push(int x) {
        StackIn.push(x);

    }

    public int pop() {
        dumpstackIn();
        return StackOut.pop();
    }

    public int peek() {

        dumpstackIn();
        return StackOut.peek();

    }

    public boolean empty() {

        return StackIn.isEmpty() && StackOut.isEmpty();

    }

    //判断输出栈是否为空，如果为空，把输入栈的元素全部放入输出栈中
    private void dumpstackIn()
    {
        if(!StackOut.isEmpty())  return ;
        while(!StackIn.isEmpty())
        {
            StackOut.push(StackIn.pop());
        }
    }

}

4、用队列实现栈

用一个队列来实现栈的操作，弹出栈或者得到栈顶元素的时候，把队列的前n-1和元素重新插到队尾，然后出队

class MyStack {

    // 用一个队列来实现栈的操作
    Queue<Integer> queue;

    public MyStack() {
        queue= new LinkedList<>();
    }

    public void push(int x) {
        queue.add(x);
    }

    public int pop() {
        RePosition();
        return queue.poll();
    }

    public int top() {
        RePosition();
        int result =queue.poll();
        queue.add(result);
        return result;
    }

    public boolean empty() {
        return queue.isEmpty();

    }
    //把队列的前n-1和元素重新插到队尾
    private void RePosition()
    {
        int size =queue.size();
        size--;
        while(size>0)
        {
            queue.add(queue.poll());
            size--;
        }
    }
}

20、有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

首先应该明确三种不匹配的情况：

第一种情况，字符串里左方向的括号多余了，所以不匹配。

第二种情况，括号没有多余，但是括号的类型没有匹配上。

第三种情况，字符串里右方向的括号多余了，所以不匹配。

即：

第一种情况：已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false

第二种情况：遍历字符串匹配的过程中，发现栈里没有要匹配的字符。所以return false

第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号return false

那么什么时候说明左括号和右括号全都匹配了呢，就是字符串遍历完之后，栈是空的，就说明全都匹配了。

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for(int i=0;i<s.length();i++)
        {
            //如果是左括号，就把相应的右括号入栈,这样后面碰见右括号直接和栈顶元素比较是否相等就可以了，不需要再分情况讨论。
            char ch=s.charAt(i);
            if(ch=='(')  stack.push(')');
            else if(ch=='{')    stack.push('}');
            else if(ch=='[')  stack.push(']');
                //其余是右括号
            else{
                //第三种情况，栈为空
                if(stack.isEmpty())
                    return false;
                    //第二种情况:括号不匹配
                else if(ch!=stack.peek())
                    return false; 
                else if(ch==stack.peek())
                    stack.pop();
            }
        }
        if(stack.isEmpty())
            return true;
            //第一种情况：遍历完成后栈不为空
        else
            return false;

    }
}

1047、删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

方法一：使用栈

class Solution {
    public String removeDuplicates(String s) {
        //使用栈，判断当前元素与上一个元素是否相等
        Stack<Character> stack =new Stack<>();

        char ch;
        for(int i=0;i<s.length();i++)
        {
            ch=s.charAt(i);
            //等于空或者不相等
            if(stack.isEmpty() || stack.peek()!=ch)
                stack.push(ch);
            else if(!stack.isEmpty() && stack.peek()==ch)
            {
                stack.pop();
            }

        }

        //用字符串拼接的方法

        // String str= "";
        // while(!stack.isEmpty()) 
        //  {
        //      str=stack.pop()+ str;   //使用string加在前面
        //}

        //用一个数组从后往前接收
        int n=stack.size();
        char[] chars =new char[n];
        n--;
        while(!stack.isEmpty())
        {
            chars[n--]=stack.pop();
        }
        return new String(chars);  

    }
}

方法二：使用StringBuilder来代替栈：

class Solution {
    public String removeDuplicates(String s) {
        //使用StringBuilder来代替栈
        StringBuilder sb =new StringBuilder();
        int top=-1; //充当栈指针
        char ch;
        for(int i=0;i<s.length();i++)
        {
            ch=s.charAt(i);
            if(top>=0 && ch==sb.charAt(top))
            {
                sb.deleteCharAt(top);
                top--;
            }
            else
            {   
                sb.append(ch);
                top++;
            }
        }
        return sb.toString();    
    }
}

方法三：使用双指针

class Solution {
    public String removeDuplicates(String s) {
        //使用双指针
        char[] chars=s.toCharArray();
        int slow=0;
        for(int fast=0;fast<chars.length;fast++)
        {
            //因为移动新元素后还有可能消除，所以先覆盖，再判断，即本题是在新的数组上进行判断比较的
            chars[slow]=chars[fast];
            if(slow>0 && chars[slow]==chars[slow-1])
                slow--;
            else
                slow++;
        }
        return new String(chars,0,slow);
    }
}

150、逆波兰表达式求值

给你一个字符串数组 tokens ，表示一个根据逆波兰表示法表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

class Solution {
    public int evalRPN(String[] tokens) {

        Stack<Integer> stack =new Stack<>();
        for(String s:tokens)
        {
            if(s.equals("+")) stack.push(stack.pop()+stack.pop());
            else if(s.equals("-")) 
                stack.push( -stack.pop()+stack.pop()); //注意先取出来的是负的
            else if(s.equals("*")) 
                stack.push(stack.pop() * stack.pop());
            else if(s.equals("/"))
            {    int temp1=stack.pop();
             int temp2=stack.pop();
             stack.push(temp2/temp1);

            }
            else{

                stack.push(Integer.valueOf(s));
            }
        }
        return stack.peek();

    }
}

Integer和String的转换

//Integer转为String
//方法一:Integer类的静态方法toString()
Integer a = 2;
String str = Integer.toString(a)

//方法二:Integer类的成员方法toString()
Integer a = 2;
String str = a.toString();

//方法三:String类的静态方法valueOf()
Integer a = 2;
String str = String.valueOf(a);

//String转为Integer
i = Integer.valueOf(str);

#239、滑动窗口的最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]

定义一个单调队列，里面维护能成为最大值的元素，当窗口滑动时，滑出的元素和单调队列的最大值，即出口元素进行比较，如果相等则弹出。

滑进的元素，和队列元素相比，如果大于队尾元素，则队尾元素出队。

class MyQueue {
    Deque<Integer> deque = new LinkedList<>();
    //弹出元素时，比较当前要弹出的数值是否等于队列出口的数值，如果相等则弹出
    //同时判断队列当前是否为空
    void poll(int val) {
        if (!deque.isEmpty() && val == deque.peek()) {
            deque.poll();
        }
    }
    //添加元素时，如果要添加的元素大于入口处的元素，就将入口元素弹出
    //保证队列元素单调递减
    //比如此时队列元素3,1，2将要入队，比1大，所以1弹出，此时队列：3,2
    void add(int val) {
        while (!deque.isEmpty() && val > deque.getLast()) {
            deque.removeLast();
        }
        deque.add(val);
    }
    //队列队顶元素始终为最大值
    int peek() {
        return deque.peek();
    }
}

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums.length == 1) {
            return nums;
        }
        int len = nums.length - k + 1;
        //存放结果元素的数组
        int[] res = new int[len];
        int num = 0;
        //自定义队列
        MyQueue myQueue = new MyQueue();
        //先将前k的元素放入队列
        for (int i = 0; i < k; i++) {
            myQueue.add(nums[i]);
        }
        res[num++] = myQueue.peek();
        for (int i = k; i < nums.length; i++) {
            //滑动窗口移除最前面的元素，移除是判断该元素是否放入队列
            myQueue.poll(nums[i - k]);
            //滑动窗口加入最后面的元素
            myQueue.add(nums[i]);
            //记录对应的最大值
            res[num++] = myQueue.peek();
        }
        return res;
    }
}

使用双端队列作为单调队列。

class Solution {
    //单调队列,维护一个单调递减队列,队头维护的是最大值
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n=nums.length;
        Deque<Integer> duque=new LinkedList<>();
        int[] ans = new int[n-k+1];
        for(int i=0;i<k;i++)
        {   
            //右边的元素如果大于左边的，那么就可以把左边的元素除去
            while(!duque.isEmpty()&& nums[i]>duque.peekLast())
            {    
                duque.pollLast();
            }
            duque.offerLast(nums[i]);         
        }
        ans[0]=duque.peekFirst();
        for(int i=k;i<n;i++)
        {
            while(!duque.isEmpty()&&nums[i]>duque.peekLast())
            {
                duque.pollLast();
            } 
            duque.offerLast(nums[i]);
            //左窗口移动，如果移动出去的是最大值，则把最大值出队
            if(duque.peekFirst()==nums[i-k])
                duque.pollFirst();
            ans[i-k+1]=duque.peekFirst();

        }  
        return ans;   
    }
}

347、前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

输入: nums = [1], k = 1
输出: [1]

思路：

要统计元素出现频率

使用一个map

对频率排序

使用优先级队列

找出前K个高频元素

优先级队列一定要制定比较规则。

利用大顶堆：时间复杂度O(n log n)

/*Comparator接口说明:
 * 返回负数，形参中第一个参数排在前面，所以从小到大的时候是第一个减去第二个；返回正数，形参中第二个参数排在前面，
 所以从大到小的时候是第二个减去第一个
 * 对于队列：排在前面意味着往队头靠
 * 对于堆（使用PriorityQueue实现）： 从队头到队尾按从小到大排就是最小堆（小顶堆），
 *                               从队头到队尾按从大到小排就是最大堆（大顶堆）--->队头元素相当于堆的根节点
 **/

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        //用大顶堆实现排序

        //map存储元素，以及元素出现的次数
        Map<Integer,Integer> map =new HashMap<>();
        for(int num:nums)
        {
            map.put(num,map.getOrDefault(num,0)+1);
        }

        //优先队列 存储数组[元素，次数]， 从大到小排，想当于大根堆
        PriorityQueue<int[]> pq =new PriorityQueue<>((pair1,pair2)->pair2[1]-pair1[1]);
        
        for(Map.Entry<Integer,Integer> entry :map.entrySet()){
            pq.add(new int[]{entry.getKey(),entry.getValue()});
        }

        int ans[] =new int [k];
        for(int i=0;i<k;i++)
        {
            ans[i]=pq.poll()[0];
        }
        return ans;

    }
}

使用大顶堆，每次需要对n大小的堆进行排序

方法二：利用小根堆，复杂度O(n log k) （重点）

只需要维持一个k大小的小顶堆，每个元素与堆顶元素比较

//解法2：基于小顶堆实现
public int[] topKFrequent2(int[] nums, int k) {
    Map<Integer,Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数
    for(int num:nums){
        map.put(num,map.getOrDefault(num,0)+1);
    }
    //在优先队列中存储二元组(num,cnt),cnt表示元素值num在数组中的出现次数
    //出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)
    PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2)->pair1[1]-pair2[1]);
    for(Map.Entry<Integer,Integer> entry:map.entrySet()){//小顶堆只需要维持k个元素有序
        if(pq.size()<k){//小顶堆元素个数小于k个时直接加
            pq.add(new int[]{entry.getKey(),entry.getValue()});
        }else{
            if(entry.getValue()>pq.peek()[1]){//当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)
                pq.poll();//弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了
                pq.add(new int[]{entry.getKey(),entry.getValue()});
            }
        }
    }
    int[] ans = new int[k];
    for(int i=k-1;i>=0;i--){ //依次弹出小顶堆,先弹出的是堆的根,出现次数少,后面弹出的出现次数多
        ans[i] = pq.poll()[0];
    }
    return ans;
}
}

总结：两大利器：单调队列和优先级队列

215、数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

提示：

1 <= k <= nums.length <= 105
-104 <= nums[i] <= 104

方法一：使用大根堆

时间复杂度：O(NlogN)，遍历数据 O(N)，堆内元素调整 O(logN)；
空间复杂度：O(N)

class Solution {
    public int findKthLargest(int[] nums, int k) {
        //优先级队列，从大到小排列
        PriorityQueue<Integer> queue =new PriorityQueue<>((num1,num2)->num2-num1);
        for(int i=0;i<nums.length;i++)
        {
            queue.add(nums[i]);    //复杂度nlogn
        }
        //把前k-1大个元素除去
        for(int i=0;i<k-1;i++)
        {
            queue.poll();
        }
        return queue.peek();
    }
}

方法二：使用小根堆

时间复杂度：O(NlogK)，遍历数据 O(N)，堆内元素调整 O(logK)；
空间复杂度：O(K)

class Solution {
    public int findKthLargest(int[] nums, int k) {
    
    PriorityQueue<Integer> pq =new PriorityQueue<>((num1,num2)->num1-num2);
    for(int num:nums){ 
        if(pq.size()<k){    //使用最小堆，堆不满时，就添加元素，堆满时，如果元素大于最小的元素，就弹出并把这个元素加入，
                            //因为找的是前k个最大的值，如果元素比堆中最小值还小，就没必要添加
            pq.add(num);
        }else{
            if(num>pq.peek()){ //当前元素大于堆中最小的一个
                pq.poll();
                pq.add(num);
            }
        }
    }
        return pq.peek();  //此时堆中就是前k个最大的值，因为是最小堆，所以第一个就是第k个最大的值。


    }
}

方法三：基于快速排序的快速选择

快速排序的核心包括“哨兵划分” 和 “递归” 。

哨兵划分：以数组某个元素（一般选取首元素）为基准数，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

递归：对左子数组和右子数组递归执行哨兵划分，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。

下图展示了数组 [2,4,1,0,3,5] 的快速排序流程。

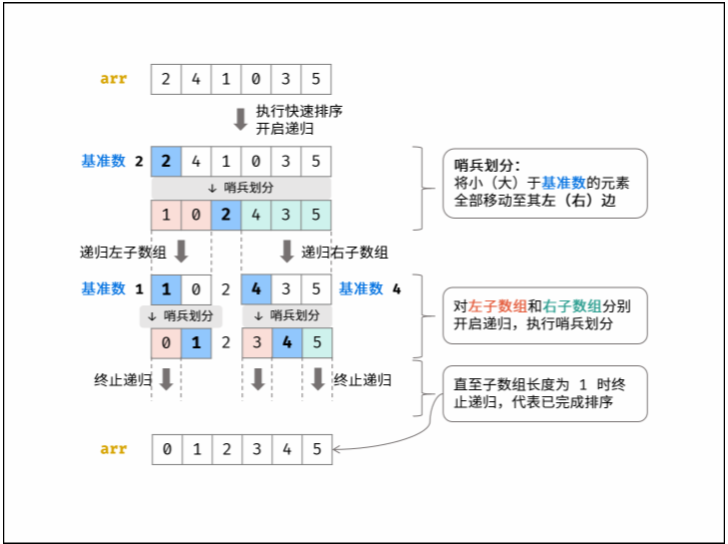
「快速选择」：设 N 为数组长度。根据快速排序原理，如果某次哨兵划分后，基准数的索引正好是 N−k ，则意味着它就是第 k 大的数字。此时就可以直接返回它，无需继续递归下去了。

我们知道快速排序的性能和「划分」出的子数组的长度密切相关。直观地理解如果每次规模为 n 的问题我们都划分成 1 和 n−1，每次递归的时候又向 n−1 的集合中递归，这种情况是最坏的，时间代价是 O(n2)。我们可以引入随机化来加速这个过程，它的时间代价的期望是 O(n)，证明过程可以参考「《算法导论》9.2：期望为线性的选择算法」。需要注意的是，这个时间复杂度只有在随机数据下才成立，而对于精心构造的数据则可能表现不佳。

使用「三路划分」，即每轮将数组划分为三个部分：小于、等于和大于基准数的所有元素。这样当发现第 k 大数字处在“等于基准数”的子数组中时，便可以直接返回该元素。

class Solution {
    public int findKthLargest(int[] nums, int k) {
       List<Integer> numList =new ArrayList<>();
       for(int num:nums)
       {
            numList.add(num);
       }
       return quickSelect(numList,k);
    }
    public int quickSelect(List<Integer> nums,int k)
    {
        Random rand=new Random();
        int pivot =nums.get(rand.nextInt(nums.size())); 
                                //在0-nums.size()-1中生成随机数
        List<Integer> smail=new ArrayList<>();
        List<Integer> equal =new ArrayList<>();
        List<Integer> big=new ArrayList<>();
        for(int num:nums)
        {
            if(num>pivot)
                big.add(num);
            else if(num<pivot)
                smail.add(num);
            else
                equal.add(num);
        }
        if(k<=big.size())
            return quickSelect(big,k);
        else if(big.size()+equal.size()<k)
            return quickSelect(smail,k-big.size()-equal.size());
        else  //第k大元素在equal中, 返回pivot
            return pivot;
    }
}

295、数据流的中位数

中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。

例如 arr = [2,3,4] 的中位数是 3 。
例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。

实现 MedianFinder 类:

MedianFinder() 初始化 MedianFinder 对象。
void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。

class MedianFinder {

    PriorityQueue<Integer> queMin;  //记录小于中位数的数
    PriorityQueue<Integer> queMax;  //记录大于中位数的数

    //当累计添加的数的数量为奇数时。
    //queMin中的数的数量比 queMax多一个
    //此时中位数为 queMin的对头
    //当累计添加的数的数量为偶数时，两个优先队列中的数的数量相同，
    //此时中位数为它们的队头的平均值。

    //维护两个队列，来使得数保持有序的分开存储
    public MedianFinder() {
        queMin = new PriorityQueue<Integer>((a, b) -> (b - a));  //从大到小
        queMax = new PriorityQueue<Integer>((a, b) -> (a - b));  //从小到大
    }
    
    public void addNum(int num) {
        if(queMin.isEmpty() ||num<=queMin.peek())  //
        {
            queMin.add(num);
            if(queMin.size()>queMax.size()+1)   //保持queMin比queMax多一个或者相等
                queMax.add(queMin.poll());
        }
        else
        {
            queMax.add(num);
            if(queMax.size()>queMin.size())
                queMin.add(queMax.poll());
        }

    }

    public double findMedian() {
        if(queMin.size()>queMax.size())
            return queMin.peek();
        return (queMin.peek()+queMax.peek()) /2.0;

    }
}

394、字符串编码

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

示例 1：

输入：s = "3[a]2[bc]"
输出："aaabcbc"

示例 2：

输入：s = "3[a2[c]]"
输出："accaccacc"

示例 3：

输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"

示例 4：

输入：s = "abc3[cd]xyz"
输出："abccdcdcdxyz"

class Solution {
    public String decodeString(String s) {
        int k=0;
        StringBuilder res=new StringBuilder();  //保存结果
        Stack<Integer> kstack=new Stack<>();
        Stack<StringBuilder> restack=new Stack<>();

        for(char c:s.toCharArray())
        {
            if(c=='[')   //碰到左括号，记录k和当前的res，并归零
            {
                kstack.push(k);
                restack.push(res);
                k=0;
                res=new StringBuilder();
            }
            else if(c==']')
                //遇到右括号，出栈最近的一个k，即左括号之前的栈，并重复计算
            {
                int curk=kstack.pop();
                StringBuilder temp=new StringBuilder();
                //重复计算括号内的字符
                for(int i=0;i<curk;i++)
                {
                    temp.append(res);
                }
                res=restack.pop().append(temp);
            }
            else if(c>='0' && c<='9')
            {
                k=c-'0'+k*10;
            }
            else{
                //如果是字母就添加
                res.append(c);
            }
        } 
        return res.toString();
    }
}

155、最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。

示例 1:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

按照上面的思路，我们只需要设计一个数据结构，使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。因此我们可以使用一个辅助栈，与元素栈同步插入与删除，用于存储与每个元素对应的最小值。

当一个元素要入栈时，我们取当前辅助栈的栈顶存储的最小值，与当前元素比较得出最小值，将这个最小值插入辅助栈中；

当一个元素要出栈时，我们把辅助栈的栈顶元素也一并弹出；

在任意一个时刻，栈内元素的最小值就存储在辅助栈的栈顶元素中。

class MinStack {
    Deque<Integer> stack;
    Deque<Integer> minstack;   //记录与栈相对应的最小值
    public MinStack() {
        stack=new LinkedList<>();
        minstack=new LinkedList<>();
        minstack.push(Integer.MAX_VALUE);
    }

    public void push(int val) {
        stack.push(val);
        minstack.push(Math.min(minstack.peek(),val)); //最小值队列中相当于存储的是元素a之前 对应的栈的最小值
    }

    public void pop() {
        stack.pop();
        minstack.pop();
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return minstack.peek();
    }
}