磁盘存储链式结构—

红黑树处理数据都是在内存中，考虑的都是内存中的运算时间复杂度。如果我们要操作的数据集非常大，大到内存已经没办法处理了该怎么办呢？
试想一下，为了要在一个拥有几十万个文件的磁盘中查找一个文本文件，设计的算法需要读取磁盘（磁盘寻址）上万次还是读取几十次，这是有本质差异的，此时为了降低对外存设备的访问次数，我们就需要新的数据结构来处理这样的问题，B树B+树（n叉树）。

B树、B+树的本质是通过降低树的层高，减少对磁盘访问次数，来提升查询速度，查找复杂度logm(n/m),m是叉的数量

B树与B+树区别与联系

B树所有节点即存储key也存储value，内存中存不下后存磁盘，名称为B-Tree，并没有B-树这种叫法
B+树只有在叶子节点存储数据value（叶子节点放在磁盘中），非叶子节点用来做索引key（非叶子结点在内存中），相比于B树，B+树更适合做磁盘索引，在大数据的存储和查找中使用较多，比如海量图像查找引擎
B树和B+树的结点添加、删除、查询基本相同

B树的性质

每个结点最多有m棵子树。
具有k个子树的非叶结点包含k -1个键。
每个非叶子结点（除了根）具有至少⌈ m/2⌉子树，即最少有⌈ m/2⌉-1个关键字。
如果根不是终端结点，则根结点至少有一个关键字，即至少有2棵子树。【根的关键字取值范围是[1，m-1]，子树的取值范围是[2,m]】
所有叶子结点都出现在同一水平，没有任何信息（高度一致）。

B+树的性质

每个结点最多有m棵子树。
如果根不是终端结点，则根结点至少有一个关键字，即至少有2棵子树。【根的关键字取值范围是[1，m-1]】
每个关键字对应一棵子树（与B树的不同），具有k个子树的非叶结点包含k 个键。
每个非叶子结点（除了根）具有至少**⌈ m/2⌉子树**，即最少有**⌈m/2⌉个关键字**。
终端结点包含全部关键字及相应记录的指针，叶结点中将关键字按大小顺序排序，并且相邻叶结点按大小顺序相互链接起来。
所有分支结点（可以视为索引的索引）中金包含他的各个子节点（即下一级的索引块）中关键字最大值，及指向其子结点的指针。

B树与B+树对比

在B+树中，叶结点包含信息，所有非叶结点仅起索引作用，非叶子结点中的每个索引项只是包含了对应子树最大关键字和指向该孩子树的指针，不含有该关键字对应记录的存储地址。
在B+树中，终端结点包含全部关键字及相应记录的指针，即非终端结点出现过的关键字也会在这重复出现一次。而B树是不重复的

一、B树的定义

我们以六叉树为例：我们说的6叉树是指，每个节点最多可拥有的子树个数，6叉树每个节点最多可拥有6颗子树，而每个节点中最多存储5个数据，如下图

至于为什么插入后会是如下图形，如何插入，请观看下面b站视频。

B树(B-树) - 来由, 定义, 插入, 构建_哔哩哔哩_bilibili

//6叉树的定义
#define SUB_M   3
 
struct _btree_node{
    /*
    int keys[2 * SUB_M-1];      //最多5个关键字
    struct _btree_node *childrens[2 * SUB_M];   //最多6颗子树    6叉树
    */
 
    int *keys;      //5
    struct _btree_node **childrens;   //6
 
    int num;    //实际存储的节点数量 <= M-1
    int leaf;   //是否为叶子节点
}
 
struct _btree {
    struct _btree_node *root;
}

二、B树添加结点

B树添加结点，只会添加在叶子结点上，重点是结点满了后，会发生分裂并向父结点上位。

添加的数据都是添加在叶子节点上，不会添加到根节点或中间节点
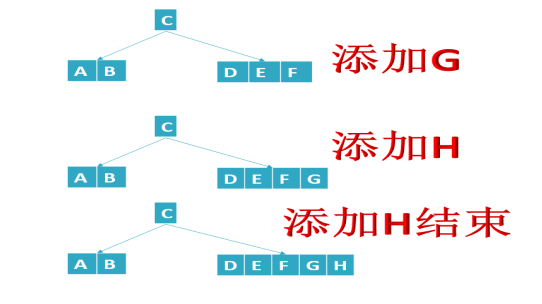
结点数据个数==M-1（结点满了的情况）,发生分裂（把(M-1)/2处数据放到父结点，其他数据分成两个结点）
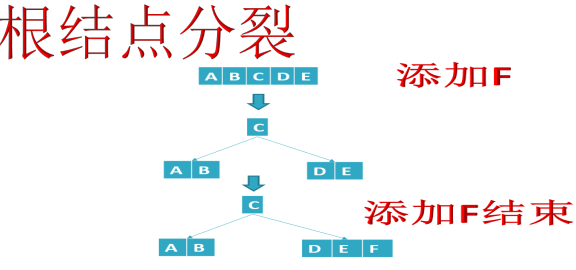
添加U，高度+1

添加结点代码如下：

/*用于结点分裂时创建新结点*/
btree_node *btree_create_node(int leaf){
    btree_node *node = (btree_node*)calloc(1, sizeof(btree_node));  //malloc需要手动清零，calloc会自动清零，set 0
    if(node == NULL) return NULL;   //在内存分配的时候一定要判断，当内存不够用的时候，malloc/calloc就会出错
 
    node->leaf = leaf;
    node->keys = calloc(2 * SUB_M -1, sizeof(int));
    node->childrens = (btree_node**)calloc(2 * SUB_M -1, sizeof(btree_node*));
    node->num = 0;
 
    return node;
}
 
/*删除结点*/
void btree_destory_node(btree_node *node){
    free(node->childrens);
    free(node->keys);
    free(node);
}
 
/*
非根结点分裂、上位：发生在B树添加元素的过程中,结点满了，需要先分裂再添加
btree *T：根节点
btree_node *x：被删除元素的父结点
int idx：位于父结点的第几颗子树
*/
void btree_split_child(btree *T, btree_node *x, int idx){
    btree_node *y = x->childrens[idx];    //满了的结点node_y
    btree_node *z = btree_create_node(y->leaf); //创建分裂后的新结点
 
    //z
    z->num = SUB_M - 1;
 
    int i=0;
    for(i=0; i < SUB_M-1; i++){
        z->keys[i] = y->keys[SUB_M+i];
    }
    if(y->leaf == 0){   //inner 是内结点，子树指针也要copy过去
        for(i=0; i < SUB_M-1; i++){
            z->childrens[i] = y->childrens[SUB_M+i];
        }
    }
 
    //y
    y->num = SUB_M;
 
    //中间元素上位
        //childrens 子树
    for(i=x->num; i >= idx+1; i--){             //寻找上为父结点的位置
        x->childrens[i+1] = x->childrens[i];    //父结点元素后移
    }
    x->childrens[i+1] = z;
        //key   
    for(i=x->num-1; i >= idx; i--){     //寻找上为父结点的位置
        x->keys[i+1] = x->keys[i];      //父结点后边元素后移 
    }
    x->keys[i] = y->keys[SUB_M];
    x->num += 1;
}
 
/*
 
*/
void btree_insert(btree *T, int key){
    btree_node *r = T->root;
    
    //根节点分裂（根节点满了）；创建一个空结点 指向root, 
    if(r->num == 2*SUB_M-1){
        btree_node *node = btree_create_node(0);
        T->root = node;
        node->childrens[0] = r;
 
        btree_split_child(T, node, 0);
    }
}

三、B树删除结点

B树删除结点，删除叶子结点和中间结点类似，重点为向父结点借位再合并操作。

先合并或者借位转换成一个B树可以删除的状态，在进行删除

删除B结点，其中路径中间结点“FI”的关键字数量为(M-1)/2-1个，为了避免以后出现资源不足的现象，需要对"FI"先进行借位合并

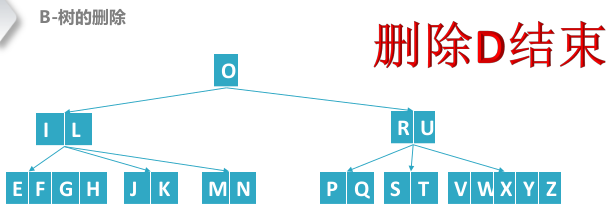
代码如下：

///b树 删除     
 
 
void btree_merge(btree *T, btree_node *x, int idx){
 
    btree_node *left = x->childrens[idx];
    btree_node *right = x->childrens[idx+1];
 
    left->keys[left->num] = x->keys[idx];
 
    int i=0;
    for(i=0; i<right->num; i++){
        left->keys[SUB_M+i] = right->keys[i];
    }
    if(!left->leaf){    //非叶子结点，要合并孩子结点指针
        for(i=0; i<SUB_M; i++){
            left->childrens[SUB_M+i] = right->childrens[i];
        }
    }
    left->num += SUB_M;
 
    btree_destory_node(right);
 
    //x key前移
    for(i=idx+1; i < x->num; i++){
        x->keys[i-1] = x->keys[i];
        x->childrens[i] = x->childrens[i+1];
    }
}

四、完整代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>

#define DEGREE		3
typedef int KEY_VALUE;

typedef struct _btree_node {
	KEY_VALUE* keys;
	struct _btree_node** childrens;
	int num;
	int leaf;
} btree_node;

typedef struct _btree {
	btree_node* root;
	int t;
} btree;

btree_node* btree_create_node(int t, int leaf) {

	btree_node* node = (btree_node*)calloc(1, sizeof(btree_node));
	if (node == NULL) assert(0);

	node->leaf = leaf;
	node->keys = (KEY_VALUE*)calloc(1, (2 * t - 1) * sizeof(KEY_VALUE));
	node->childrens = (btree_node**)calloc(1, (2 * t) * sizeof(btree_node*));
	node->num = 0;

	return node;
}

void btree_destroy_node(btree_node* node) {

	assert(node);
	free(node->keys);
	//free(node->childrens);
	free(node);
}

void btree_create(btree* T, int t) {
	T->t = t;

	btree_node* x = btree_create_node(t, 1);
	T->root = x;
}

void btree_split_child(btree* T, btree_node* x, int i) {
	int t = T->t;

	btree_node* y = x->childrens[i];
	btree_node* z = btree_create_node(t, y->leaf);

	z->num = t - 1;

	int j = 0;
	for (j = 0; j < t - 1; j++) {
		z->keys[j] = y->keys[j + t];
	}
	if (y->leaf == 0) {
		for (j = 0; j < t; j++) {
			z->childrens[j] = y->childrens[j + t];
		}
	}

	y->num = t - 1;
	for (j = x->num; j >= i + 1; j--) {
		x->childrens[j + 1] = x->childrens[j];
	}

	x->childrens[i + 1] = z;

	for (j = x->num - 1; j >= i; j--) {
		x->keys[j + 1] = x->keys[j];
	}
	x->keys[i] = y->keys[t - 1];
	x->num += 1;

}

void btree_insert_nonfull(btree* T, btree_node* x, KEY_VALUE k) {

	int i = x->num - 1;

	if (x->leaf == 1) {

		while (i >= 0 && x->keys[i] > k) {
			x->keys[i + 1] = x->keys[i];
			i--;
		}
		x->keys[i + 1] = k;
		x->num += 1;

	}
	else {
		while (i >= 0 && x->keys[i] > k) i--;

		if (x->childrens[i + 1]->num == (2 * (T->t)) - 1) {
			btree_split_child(T, x, i + 1);
			if (k > x->keys[i + 1]) i++;
		}

		btree_insert_nonfull(T, x->childrens[i + 1], k);
	}
}

void btree_insert(btree* T, KEY_VALUE key) {
	//int t = T->t;

	btree_node* r = T->root;
	if (r->num == 2 * T->t - 1) {

		btree_node* node = btree_create_node(T->t, 0);
		T->root = node;

		node->childrens[0] = r;

		btree_split_child(T, node, 0);

		int i = 0;
		if (node->keys[0] < key) i++;
		btree_insert_nonfull(T, node->childrens[i], key);

	}
	else {
		btree_insert_nonfull(T, r, key);
	}
}

void btree_traverse(btree_node* x) {
	int i = 0;

	for (i = 0; i < x->num; i++) {
		if (x->leaf == 0)
			btree_traverse(x->childrens[i]);
		printf("%C ", x->keys[i]);
	}

	if (x->leaf == 0) btree_traverse(x->childrens[i]);
}

void btree_print(btree* T, btree_node* node, int layer)
{
	btree_node* p = node;
	int i;
	if (p) {
		printf("\nlayer = %d keynum = %d is_leaf = %d\n", layer, p->num, p->leaf);
		for (i = 0; i < node->num; i++)
			printf("%c ", p->keys[i]);
		printf("\n");
#if 0
		printf("%p\n", p);
		for (i = 0; i <= 2 * T->t; i++)
			printf("%p ", p->childrens[i]);
		printf("\n");
#endif
		layer++;
		for (i = 0; i <= p->num; i++)
			if (p->childrens[i])
				btree_print(T, p->childrens[i], layer);
	}
	else printf("the tree is empty\n");
}


int btree_bin_search(btree_node* node, int low, int high, KEY_VALUE key) {
	int mid;
	if (low > high || low < 0 || high < 0) {
		return -1;
	}

	while (low <= high) {
		mid = (low + high) / 2;
		if (key > node->keys[mid]) {
			low = mid + 1;
		}
		else {
			high = mid - 1;
		}
	}

	return low;
}


//{child[idx], key[idx], child[idx+1]} 
void btree_merge(btree* T, btree_node* node, int idx) {

	btree_node* left = node->childrens[idx];
	btree_node* right = node->childrens[idx + 1];

	int i = 0;

	/data merge
	left->keys[T->t - 1] = node->keys[idx];
	for (i = 0; i < T->t - 1; i++) {
		left->keys[T->t + i] = right->keys[i];
	}
	if (!left->leaf) {
		for (i = 0; i < T->t; i++) {
			left->childrens[T->t + i] = right->childrens[i];
		}
	}
	left->num += T->t;

	//destroy right
	btree_destroy_node(right);

	//node 
	for (i = idx + 1; i < node->num; i++) {
		node->keys[i - 1] = node->keys[i];
		node->childrens[i] = node->childrens[i + 1];
	}
	node->childrens[i + 1] = NULL;
	node->num -= 1;

	if (node->num == 0) {
		T->root = left;
		btree_destroy_node(node);
	}
}

void btree_delete_key(btree* T, btree_node* node, KEY_VALUE key) {

	if (node == NULL) return;

	int idx = 0, i;

	while (idx < node->num && key > node->keys[idx]) {
		idx++;
	}

	if (idx < node->num && key == node->keys[idx]) {

		if (node->leaf) {

			for (i = idx; i < node->num - 1; i++) {
				node->keys[i] = node->keys[i + 1];
			}

			node->keys[node->num - 1] = 0;
			node->num--;

			if (node->num == 0) { //root
				free(node);
				T->root = NULL;
			}

			return;
		}
		else if (node->childrens[idx]->num >= T->t) {

			btree_node* left = node->childrens[idx];
			node->keys[idx] = left->keys[left->num - 1];

			btree_delete_key(T, left, left->keys[left->num - 1]);

		}
		else if (node->childrens[idx + 1]->num >= T->t) {

			btree_node* right = node->childrens[idx + 1];
			node->keys[idx] = right->keys[0];

			btree_delete_key(T, right, right->keys[0]);

		}
		else {

			btree_merge(T, node, idx);
			btree_delete_key(T, node->childrens[idx], key);

		}

	}
	else {

		btree_node* child = node->childrens[idx];
		if (child == NULL) {
			printf("Cannot del key = %d\n", key);
			return;
		}

		if (child->num == T->t - 1) {

			btree_node* left = NULL;
			btree_node* right = NULL;
			if (idx - 1 >= 0)
				left = node->childrens[idx - 1];
			if (idx + 1 <= node->num)
				right = node->childrens[idx + 1];

			if ((left && left->num >= T->t) ||
				(right && right->num >= T->t)) {

				int richR = 0;
				if (right) richR = 1;
				if (left && right) richR = (right->num > left->num) ? 1 : 0;

				if (right && right->num >= T->t && richR) { //borrow from next
					child->keys[child->num] = node->keys[idx];
					child->childrens[child->num + 1] = right->childrens[0];
					child->num++;

					node->keys[idx] = right->keys[0];
					for (i = 0; i < right->num - 1; i++) {
						right->keys[i] = right->keys[i + 1];
						right->childrens[i] = right->childrens[i + 1];
					}

					right->keys[right->num - 1] = 0;
					right->childrens[right->num - 1] = right->childrens[right->num];
					right->childrens[right->num] = NULL;
					right->num--;

				}
				else { //borrow from prev

					for (i = child->num; i > 0; i--) {
						child->keys[i] = child->keys[i - 1];
						child->childrens[i + 1] = child->childrens[i];
					}

					child->childrens[1] = child->childrens[0];
					child->childrens[0] = left->childrens[left->num];
					child->keys[0] = node->keys[idx - 1];

					child->num++;

					node->keys[idx - 1] = left->keys[left->num - 1];
					left->keys[left->num - 1] = 0;
					left->childrens[left->num] = NULL;
					left->num--;
				}

			}
			else if ((!left || (left->num == T->t - 1))
				&& (!right || (right->num == T->t - 1))) {

				if (left && left->num == T->t - 1) {
					btree_merge(T, node, idx - 1);
					child = left;
				}
				else if (right && right->num == T->t - 1) {
					btree_merge(T, node, idx);
				}
			}
		}

		btree_delete_key(T, child, key);
	}

}

int btree_delete(btree* T, KEY_VALUE key) {
	if (!T->root) return -1;

	btree_delete_key(T, T->root, key);
	return 0;
}

int main() {
	btree T = { 0 };

	btree_create(&T, 3);
	srand(48);

	int i = 0;
	char key[27] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
	for (i = 0; i < 26; i++) {
		//key[i] = rand() % 1000;
		printf("%c ", key[i]);
		btree_insert(&T, key[i]);
	}

	btree_print(&T, T.root, 0);

	for (i = 0; i < 26; i++) {
		printf("\n---------------------------------\n");
		btree_delete(&T, key[25 - i]);
		//btree_traverse(T.root);
		btree_print(&T, T.root, 0);
	}
}