博主主页:Cool Kid~Yu仙笙_C++领域博主🦄
目录
二分查找定义
二分查找效率
二分查找与遍历的对比
二分查找的限制性
二分查找的限制性(总结)
二分查找搭建
循环实现二分查找
循环二分查找基本框架:
循环二分查找源码:
递归实现二分查找
递归二分查找基本框架:
递归二分查找源码:
C++二分查找例题【小试牛刀】
一元三次方程求解
解析:
源码:
C++二分查找例题【步入神坛】
字符串
解析:【此题非一般人可看(通俗说就是不全是二分查找的问题,跑题了)】
源码:
二分查找定义
二分查找又称折半查找(Binary Search),优点是比较次数少,查找速度快,平均性能好,占用系统内存较少;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
二分查找效率
二分查找是啥上面已经说明,现在我们来了解二分查找的效率
二分查找的时间复杂程度是
查找速度有多快呢?我们来实验一下。
---------------------------------------------------------------------------------------------------------------------------------
我们假设数据大小是 n,每次查找后数据都会缩小为原来的一半,也就是会除以 2。最坏情况下,直到查找区间被缩小为空,才停止。
就因为这种特性,有的时候甚至比时间复杂度是常量级 O(1) 的算法还要高效。为什么这么说呢?
因为 logn 是一个非常“恐怖”的数量级,即便 n 非常非常大,对应的 logn 也很小。比如 n 等于 2 的 32 次方,这个数很大了吧?大约是 42 亿。也就是说,如果我们在 42 亿个数据中用二分查找一个数据,最多需要比较 32 次。
---------------------------------------------------------------------------------------------------------------------------------
二分查找与遍历的对比
上面也是讲述了二分查找的效率,不够直观,我们可以将二分查找与遍历进行一个对比,就能直观的看出二分查找在速度方面上的优势了
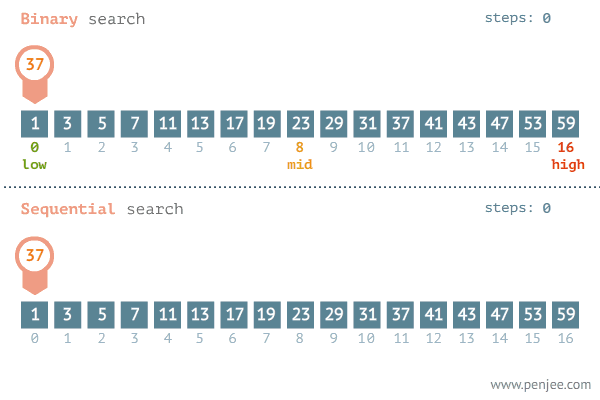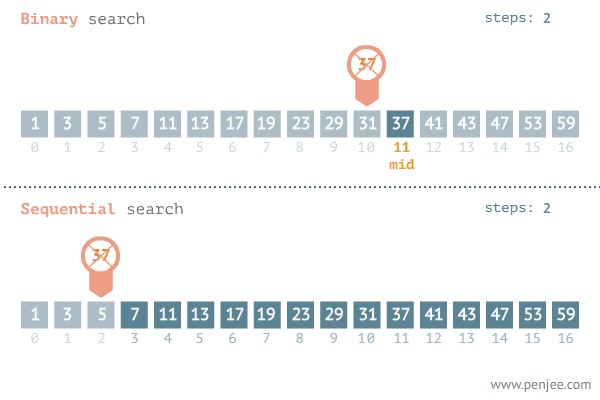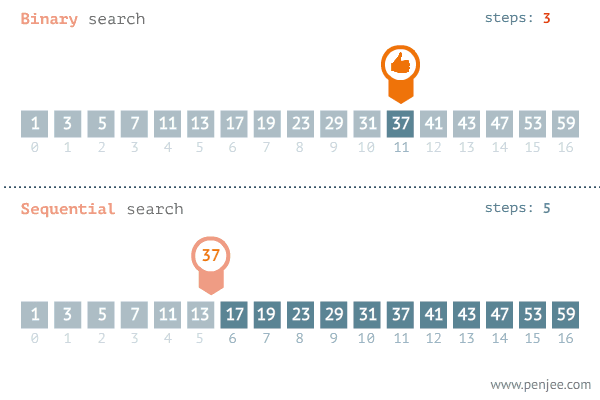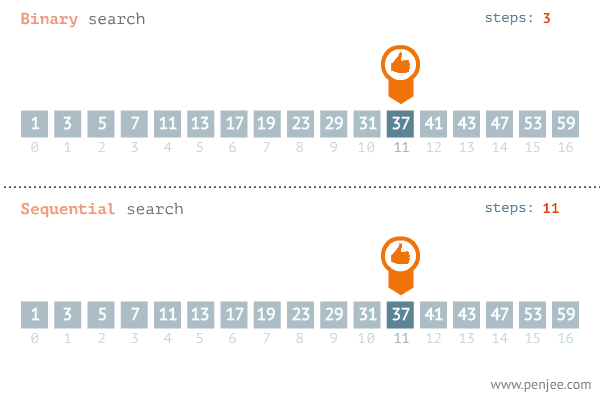
从图中可以看出二分查找用了三步就找到了查找值,而遍历则用了11步才找到查找值,可见二分查找的效率非常之高。
---------------------------------------------------------------------------------------------------------------------------------
刚刚我们对比讲述了一下二分查找的优点,现在讲讲二分查找的局限(该如何正确选择使用二分查找)
二分查找的限制性
1. 二分查找需要利用下标随机访问元素,如果我们想使用链表等其他数据结构则无法实现二分查找。这就说明,二分查找依赖数组结构
-----------------------------------------------------------------------------------------------------------------------
2.二分查找需要的数据必须是有序的。如果数据没有序,我们需要先排序,排序的时间复杂度最低是 O(nlogn)。所以,如果我们针对的是一组静态的数据,没有频繁地插入、删除,我们可以进行一次排序,多次二分查找。这样排序的成本可被均摊,二分查找的边际成本就会比较低。但是,如果我们的数据集合有频繁的插入和删除操作,要想用二分查找,要么每次插入、删除操作之后保证数据仍然有序,要么在每次二分查找之前都先进行排序。针对这种动态数据集合,无论哪种方法,维护有序的成本都是很高的。所以,二分查找只能用在插入、删除操作不频繁,一次排序多次查找的场景中。针对动态变化的数据集合,二分查找将不再适用,这就说明了,二分查找针对的是有序数据
-------------------------------------------------------------------------------------------------------------------------
3.如果要处理的数据量很小,完全没有必要用二分查找,顺序遍历就足够了。比如我们在一个大小为 10 的数组中查找一个元素,不管用二分查找还是顺序遍历,查找速度都差不多,只有数据量比较大的时候,二分查找的优势才会比较明显。,这就说明了,二分查找不适合数据量太小
-------------------------------------------------------------------------------------------------------------------------
4.二分查找底层依赖的是数组,数组需要的是一段连续的存储空间,所以我们的数据比较大时,比如1GB,这时候可能不太适合使用二分查找,因为我们的内存都是离散的,电脑内存可能没有那么多。这就说明了,数据量太大不适合二分查找
-------------------------------------------------------------------------------------------------------------------------
二分查找的限制性(总结)
- 二分查找依赖数组结构
- 二分查找针对的是有序数据
- 二分查找不适合数据量太小
- 数据量太大不适合二分查找
二分查找搭建
二分查找有两种实现方式,接下来依次展开说明
- 循环
- 递归
循环实现二分查找
循环二分查找基本框架:
int BinarySearch(int arr[], int len, int target) {
int low = 0;
int high = len;
int mid = 0;
while (low <= high) {
mid = (low + high) / 2;
if (target < arr[mid]) high = mid - 1;
else if (target > arr[mid]) low = mid + 1;
else return mid;
}
return -1;
}循环二分查找源码:
#include<iostream>
using namespace std;
int BinarySearch(int arr[], int len, int target) {
int low = 0;
int high = len;
int mid = 0;
while (low <= high) {
mid = (low + high) / 2;
if (target < arr[mid]) high = mid - 1;
else if (target > arr[mid]) low = mid + 1;
else return mid;
}
return -1;
}
int main() {
int array[] = { 7,14,18,21,23,29,31,5,38,42,46,49,52 };
int arrayLen = sizeof(array) / sizeof(array[0]);
int index = BinarySearch(array, arrayLen, 52);
if (index != -1) {
cout << "查找" << array[index] << "成功";
}
else {
cout << "查找失败";
}
return 0;
}递归实现二分查找
递归二分查找基本框架:
int BinarySearch(int arr[], int low, int high, int target) {
if (low > high)return -1;
else {
int mid = (low + high) / 2;
if (target < arr[mid]) return BinarySearch(arr, low, mid - 1, target);
else if (target > arr[mid]) return BinarySearch(arr, mid + 1, high, target);
else return mid;
}
}递归二分查找源码:
#include<iostream>
using namespace std;
int BinarySearch(int arr[], int low, int high, int target) {
if (low > high)return -1;
else {
int mid = (low + high) / 2;
if (target < arr[mid]) return BinarySearch(arr, low, mid - 1, target);
else if (target > arr[mid]) return BinarySearch(arr, mid + 1, high, target);
else return mid;
}
}
int main() {
int array[] = { 7,14,18,21,23,29,31,5,38,42,46,49,52 };
int arrayLen = sizeof(array) / sizeof(array[0]);
int index = BinarySearch(array, 0, arrayLen, 52);
if (index != -1) {
cout << "查找" << array[index] << "成功";
}
else {
cout << "查找失败";
}
return 0;
}现在,大家或多或少已经了解二分查找以及使用了,那么现在,我们就可以去小试牛刀了
---------------------------------------------------------------------------------------------------------------------------------
C++二分查找例题【小试牛刀】
一元三次方程求解
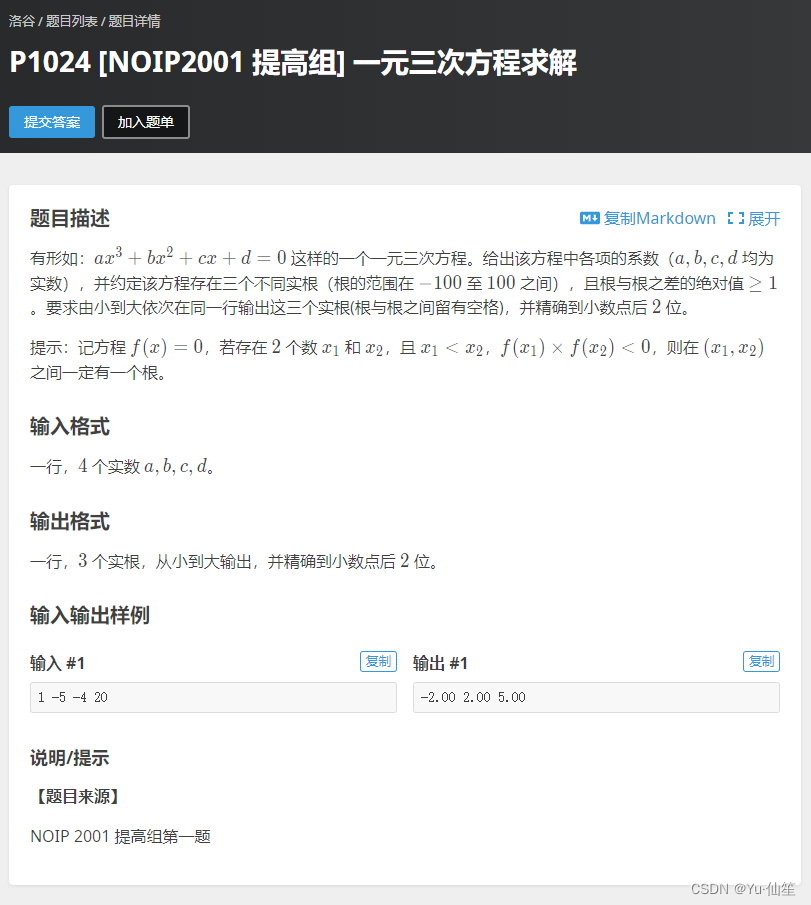
解析:
这道题符合了运用二分查找的四个条件,所以直接运用即可,难度低
源码:
#include<cstdio>
double a,b,c,d;
double fc(double x)
{
return a*x*x*x+b*x*x+c*x+d;
}
int main()
{
double l,r,m,x1,x2;
int s=0,i;
scanf("%lf%lf%lf%lf",&a,&b,&c,&d); //输入
for (i=-100;i<100;i++)
{
l=i;
r=i+1;
x1=fc(l);
x2=fc(r);
if(!x1)
{
printf("%.2lf ",l);
s++;
} //判断左端点,是零点直接输出。
//不能判断右端点,会重复。
if(x1*x2<0) //区间内有根。
{
while(r-l>=0.001) //二分控制精度。
{
m=(l+r)/2; //middle
if(fc(m)*fc(r)<=0)
l=m;
else
r=m; //计算中点处函数值缩小区间。
}
printf("%.2lf ",r);
//输出右端点。
s++;
}
if (s==3)
break;
//找到三个就退出大概会省一点时间
}
return 0;
}相信经过这一道题的练手,大家都能熟练运用了,那么接下来,就让我们进入在二分查找自由翱翔的进阶吧
C++二分查找例题【步入神坛】
字符串

解析:【此题非一般人可看(通俗说就是不全是二分查找的问题,跑题了)】
设我们的答案为mid(注意这里有坑是[a,b]的所有子串和[c,d]这个子串的最长lcp),那么我们会发现一个很有趣的事实: 如果mid可行的话,那么任意一个比mid小的数也可行
也就是说,问题满足可二分性,那么我们可以二分答案,将原问题转化为一个判定性问题:mid这个答案行不行?
那么我们发现,如果mid这个答案可以的话,就会存在一个后缀S,
1.它的开头在[a,b-mid+1]当中。
2.lcp(S,c)>=mid。
再次转化一步,就是询问满足以上两个条件的后缀S的个数,经典的二元限制统计问题,我们的思路很简单,摁死一个再去管下一个,发现一件有趣的事实:如果把这些后缀排好序,那么lcp符合要求的一定是一段连续的区间,(为什么?,因为我们发现排好序以后,lcp这个函数是单峰的,并且峰值在自己这里)
那么我们似乎可以二分左端点和右端点,为此我们需要O(1)求出区间最小值,为此我们还得写一个St表QAQ
那么最后我们发现现在两个限制都是区间型的了,而且是静态区间,没有修改,所以可以用主席树查询一发……
源码:
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
const int N=100010;int n;int m;
char mde[N];int sa[N];int rk[2*N];int ht[N];
int x[N];int y[N];queue <int> q[N];
inline bool cmp(int i,int j){return (x[i]==x[j])&&(y[i]==y[j]);}
inline void rixs()//这里的后缀数组用的是队列实现,常数较大
{
for(int i=1;i<=n;i++){q[y[i]].push(i);}
int cnt=0;for(int i=0;i<=n;i++)
{for(;!q[i].empty();q[i].pop()){sa[++cnt]=q[i].front();}}
for(int i=1;i<=n;i++){q[x[sa[i]]].push(sa[i]);}
cnt=0;for(int i=0;i<=n;i++)
{for(;!q[i].empty();q[i].pop()){sa[++cnt]=q[i].front();}}
rk[sa[1]]=1;for(int i=2;i<=n;i++)
{rk[sa[i]]=(cmp(sa[i-1],sa[i]))?rk[sa[i-1]]:i;}
}
inline void create_sa()//板子啥的问度娘吧
{
for(int i=1;i<=n;i++){q[mde[i]-'a'+1].push(i);}
int cnt=0;for(int i=1;i<=26;i++)
{for(;!q[i].empty();q[i].pop()){sa[++cnt]=q[i].front();}}
rk[sa[1]]=1;for(int i=2;i<=n;i++)
{rk[sa[i]]=(mde[sa[i-1]]==mde[sa[i]])?rk[sa[i-1]]:i;}
for(int k=1;k<=n;k*=2)
{for(int i=1;i<=n;i++){x[i]=rk[i];y[i]=rk[i+k];}rixs();}
}
inline void calch()
{
int j=0;int k=0;for(int i=1;i<=n;ht[rk[i++]]=k)
{for(k=k?k-1:k,j=sa[rk[i]-1];mde[i+k]==mde[j+k];k++);}
}
int st[22][N];int log[N];
inline void calclog()//打表log,方便使用
{int i=0;for(int j=1;j<=n;j++){if((1<<(i+1))<=j)i++;log[j]=i;}}
inline void create_st()//对ht建st表
{
for(int i=0;i<=n-1;i++){st[0][i]=ht[i+1];}
for(int i=1;i<=log[n];i++)
{for(int j=0;j<n-(1<<(i-1));j++){st[i][j]=min(st[i-1][j],st[i-1][j+(1<<(i-1))]);}}
}
inline int rmq(int l,int r)//左开右闭的rmq
{int len=r-l;int res=min(st[log[len]][l],st[log[len]][r-(1<<log[len])]);return res;}
struct per_linetree//主席树的板子,这个真的是纯板子了
{
int s[2][44*N];int fa[44*N];int root[N];int cnt;int val[44*N];
per_linetree(){root[0]=1;cnt=1;}
inline void insert(int p1,int p2,int l,int r,int pos)
{
val[p2]=val[p1]+1;if(r-l==1)return;int mid=(l+r)/2;
if(pos<=mid){s[0][p2]=++cnt;s[1][p2]=s[1][p1];insert(s[0][p1],cnt,l,mid,pos);}
else {s[1][p2]=++cnt;s[0][p2]=s[0][p1];insert(s[1][p1],cnt,mid,r,pos);}
}
inline void add(int t1,int t2,int pos)
{root[t2]=++cnt;insert(root[t1],root[t2],0,n,pos);}
inline int sum(int p1,int p2,int l,int r,int dl,int dr)
{
if(dl==l&&dr==r){return val[p2]-val[p1];}int mid=(l+r)/2;int res=0;
if(dl<mid)res+=sum(s[0][p1],s[0][p2],l,mid,dl,min(dr,mid));
if(mid<dr)res+=sum(s[1][p1],s[1][p2],mid,r,max(dl,mid),dr);
return res;
}
inline int query(int t1,int t2,int l,int r)
{return sum(root[t1-1],root[t2],0,n,l-1,r);}
}plt;
inline bool jud(int x,int a,int b,int c)//检测mid是否可行
{
int l=1;int r=rk[c];int up;int down;//二分上边界,注意是左开右闭
while(l<r){int mid=(l+r)/2;if(rmq(mid,rk[c])<x){l=mid+1;}else {r=mid;}}
up=r;
l=rk[c];r=n;//二分下边界
while(l<r){int mid=(l+r+1)/2;if(rmq(rk[c],mid)<x){r=mid-1;} else{l=mid;}}
down=r;
return plt.query(up,down,a,b-x+1)!=0;//主席树查一发是否存在符合要求的后缀
}
inline int solve(int a,int b,int c,int d)//主二分过程
{
int l=0;int r=min(b-a+1,d-c+1);//这个就是裸的二分答案了
while(l<r){int mid=(l+r+1)/2;if(jud(mid,a,b,c)){l=mid;}else {r=mid-1;}}
return r;
}
int main()
{
scanf("%d%d",&n,&m);scanf("%s",mde+1);
create_sa();calch();calclog();create_st();//上来先预处理
for(int i=1;i<=n;i++){plt.add(i-1,i,sa[i]);}//对sa建主席树
for(int i=1;i<=m;i++)
{
int a;int b;int c;int d;
scanf("%d%d%d%d",&a,&b,&c,&d);
printf("%d\n",solve(a,b,c,d));
}return 0;//拿下!
}还有更多精彩内容聚焦在C++知识精讲专栏【记得订阅哦】