1.题目解析

题目来源：106.从中序和后序遍历序列构造二叉树 

测试用例

2.算法原理 

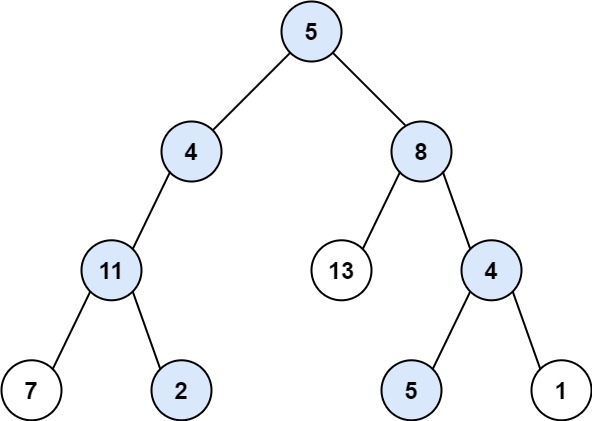
后序遍历：按照左子树->右子树->根节点的顺序遍历二叉树，也就是说最末尾的节点是最上面的根节点

中序遍历：按照左子树->根节点->右子树的顺序遍历二叉树 

题目要求按照给出的后序序列与中序序列创建二叉树，跟之前的按照前序与中序序列创建二叉树异曲同工，不同的是后序序列需要从末尾开始取出根节点将中序序列分为三个区间，然后要求先构建右子树再构建左子树，而前序则是先构建左子树再构建右子树 

3.实战代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* build(vector<int>& inorder, vector<int>& postorder,int& posti,int inbegin,int inend)
    {
        //处理叶子结点
        if(inbegin > inend)
        {
            return nullptr;
        }

        //根据后序确定根节点
        TreeNode* root = new TreeNode(postorder[posti]);

        //将中序序列分为三个区间
        //左子树 根节点 右子树
        int rooti = inbegin;
        while(inbegin <= inend)
        {
            if(inorder[rooti] == postorder[posti])
            {
                break;
            }
            rooti++;
        }
        //后序由后向前遍历
        posti--;
       
       //后序需要先构建右子树再构建左子树
        root->right = build(inorder, postorder,posti,rooti+1,inend); 
        root->left = build(inorder, postorder,posti,inbegin,rooti-1);

        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
    {
        int i = postorder.size() - 1;
        return build(inorder,postorder,i,0,inorder.size() - 1);
    }
};