目录
连续数组(medium)
题目解析
讲解算法原理
编写代码
矩阵区域和(medium)
题目解析
讲解算法原理
编写代码
连续数组(medium)
题目解析
1.题目链接:. - 力扣(LeetCode)
2.题目描述
给定⼀个⼆进制数组nums,找到含有相同数量的0和1的最⻓连续⼦数组,并返回该⼦数组的⻓度。
⽰例1:
输⼊:nums=[0,1]输出:2
说明:
[0,1]是具有相同数量0和1的最⻓连续⼦数组。⽰例2:
输⼊:nums=[0,1,0]输出:2
说明:
[0,1](或[1,0])是具有相同数量0和1的最⻓连续⼦数组。
提⽰:
1<=nums.length<=10^5
nums[i]不是0就是1
讲解算法原理
暴⼒解法就是枚举所有的⼦数组,然后判断⼦数组是否满⾜要求,这⾥不再赘述。)
解法(前缀和在哈希表中):
算法思路:
稍微转化⼀下题⽬,就会变成我们熟悉的题:
• 本题让我们找出⼀段连续的区间, 0 和 1 出现的次数相同。
• 如果将 0 记为 -1 , 1 记为 1 ,问题就变成了找出⼀段区间,这段区间的和等于 0 。
• 于是,就和560.和为K的⼦数组这道题的思路⼀样

设 i 为数组中的任意位置,⽤ sum[i] 表⽰ [0, i] 区间内所有元素的和。
想知道最⼤的「以 i 为结尾的和为 0 的⼦数组」,就要找到从左往右第⼀个 x1 使得 [x1, i] 区间内的所有元素的和为 0 。那么 [0, x1 - 1] 区间内的和是不是就是 sum[i] 了。于是问题就变成:
• 找到在 [0, i - 1] 区间内,第⼀次出现 sum[i] 的位置即可。
我们不⽤真的初始化⼀个前缀和数组,因为我们只关⼼在 i 位置之前,第⼀个前缀和等于 sum[i] 的位置。因此,我们仅需⽤⼀个哈希表,⼀边求当前位置的前缀和,⼀边记录第⼀次出现该前缀和的位置。
编写代码
c++算法代码:
class Solution
{
public:
int findMaxLength(vector<int>& nums)
{
unordered_map<int, int> hash;
hash[0] = -1; // 默认有⼀个前缀和为 0 的情况
int sum = 0, ret = 0;
for(int i = 0; i < nums.size(); i++)
{
sum += nums[i] == 0 ? -1 : 1; // 计算当前位置的前缀和
if(hash.count(sum)) ret = max(ret, i - hash[sum]);
else hash[sum] = i;
}
return ret;
}
};java算法代码:
class Solution {
public int findMaxLength(int[] nums) {
Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
hash.put(0, -1); // 默认存在⼀个前缀和为 0 的情况
int sum = 0, ret = 0;
for(int i = 0; i < nums.length; i++)
{
sum += (nums[i] == 0 ? -1 : 1); // 计算当前位置的前缀和
if(hash.containsKey(sum)) ret = Math.max(ret, i - hash.get(sum));
else hash.put(sum, i);
}
return ret;
}
}
矩阵区域和(medium)
题目解析
1.题目链接:. - 力扣(LeetCode)
2.题目描述
给你⼀个mxn的矩阵mat和⼀个整数k,请你返回⼀个矩阵answer,其中每个answer[i][j]是所有满⾜下述条件的元素mat[r][c]的和:
• i-k<=r<=i+k,
• j-k<=c<=j+k且
• (r,c)在矩阵内。
⽰例1:
输⼊:mat=[[1,2,3],[4,5,6],[7,8,9]],k=1
输出:[[12,21,16],[27,45,33],[24,39,28]]
⽰例2:
输⼊:mat=[[1,2,3],[4,5,6],[7,8,9]],k=2
输出:[[45,45,45],[45,45,45],[45,45,45]]
提⽰:
m==mat.length
n==mat[i].length
1<=m,n,k<=100
1<=mat[i][j]<=100
讲解算法原理
解法:
算法思路:
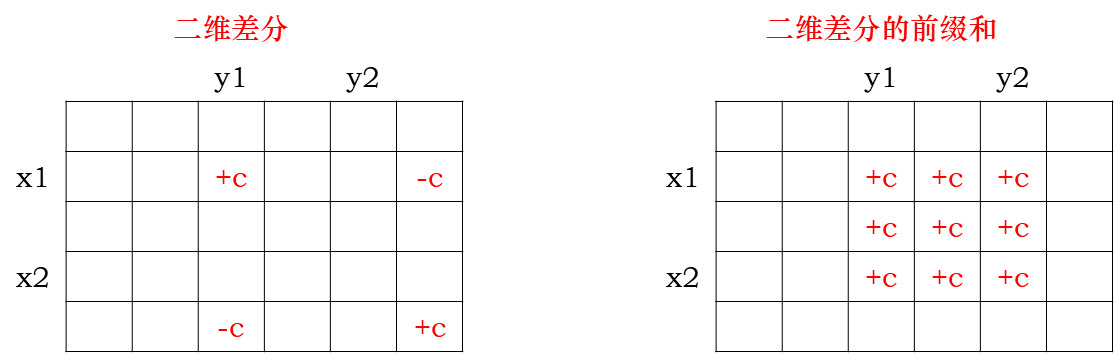
⼆维前缀和的简单应⽤题,关键就是我们在填写结果矩阵的时候,要找到原矩阵对应区域的「左上⻆」以及「右下⻆」的坐标(推荐⼤家画图)
左上⻆坐标: x1 = i - k,y1 = j - k ,但是由于会「超过矩阵」的范围,因此需要对 0 取⼀个 max 。因此修正后的坐标为: x1 = max(0, i - k), y1 = max(0, j - k) ;
右下⻆坐标: x1 = i + k,y1 = j + k ,但是由于会「超过矩阵」的范围,因此需要对 m - 1 ,以及 n - 1 取⼀个 min 。因此修正后的坐标为: x2 = min(m - 1, i + k),
y2 = min(n - 1, j + k) 。
然后将求出来的坐标代⼊到「⼆维前缀和矩阵」的计算公式上即可~(但是要注意下标的映射关系)
编写代码
c++算法代码:
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 1. 预处理前缀和矩阵
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] +
mat[i - 1][j - 1];
// 2. 使⽤
vector<vector<int>> ret(m, vector<int>(n));
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
{
int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;
int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;
ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] +
dp[x1 - 1][y1 - 1];
}
return ret;
}
};java算法代码:
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
// 1. 预处理前缀和矩阵
int[][] dp = new int[m + 1][n + 1];
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] +
mat[i - 1][j - 1];
// 2. 使⽤
int[][] ret = new int[m][n];
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
{
int x1 = Math.max(0, i - k) + 1, y1 = Math.max(0, j - k) + 1;
int x2 = Math.min(m - 1, i + k) + 1, y2 = Math.min(n - 1, j +
k) + 1;
ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] +
dp[x1 - 1][y1 - 1];
}
return ret;
}
}