题目引入

开发商小 Q 买下了一条街，他想在这条街的一边盖房子。

街道可以抽象为一条数轴，而小 Q 只会在坐标在 1~n 的范围内盖房子。

首先，小 Q 将街上坐标在 1∼ 𝑛1∼ n 范围内的物体全部铲平。也就是说，在正式动工盖房子之前，1∼ 𝑛1∼ n 范围内是没有东西的。

小 Q 的盖房子技术出奇的烂，他每次只会在坐标从 l 到 r 的一段区间上砌一堵高为 h 厘米的墙。如果某个位置已经有墙了，那么他会将墙加高 h 厘米。

好吧小 Q 不得不承认自己不会盖房子只会砌墙。

小 Q 已经砌了 m 次墙了，整条街已经乱七八糟的了。

什么是差分

差分是前缀和的逆运算，也就是说，对差分数组就是计算前缀和数组的“原数组”，例如，差分数组为：【1, 2, 3, 4, 5】，前缀和数组就是【1, 3, 6, 10, 15】。

优势

我们可以把题目中的墙当成一个前缀和数组，因为小Q每砌墙一次，就会把一段区间的数值一起加上若干厘米。

比如说，原本墙数组为：1, 0, 3, 0, 0

那么差分数组就是：1, -1, 3, -3, 0

如果我们要将2~3加上1，我们只需改变差分数组：1, 0（加一）, 3, -4(减一）, 0，对应的墙就是（前缀和）：1, 1, 4, 0, 0

所以我们更改时，只需建立一个差分数组，无需建立前缀和数组，输出时直接计算即可。

#include <bits/stdc++.h>
using namespace std;


int main() {
	int n, m, c[500005];
	memset(c, 0, sizeof (c));
	cin >> n >> m;
	while (m--) {
		int l, r, h;
		cin >> l >> r >> h;
		// 把墙数组当成前缀和来看，并建立它的逆运算差分数组
		c[l] += h;
		c[r + 1] -= h;
	}
	for (int i = 1; i <= n; i++) {
		if (i != 1)
			cout << " ";
		c[i] += c[i - 1];
		cout << c[i];
	}
	cout << endl;
	return 0;
}

二维差分

大哈有一面 n * n 的广告墙，他往墙上贴 m 张广告，广告之间有些部分会相互重叠，问墙上的每个点上覆盖了几张广告？

这题其实也是差分，贴广告，一定时覆盖了一个区域，而这个区域一定是二维上连续的。

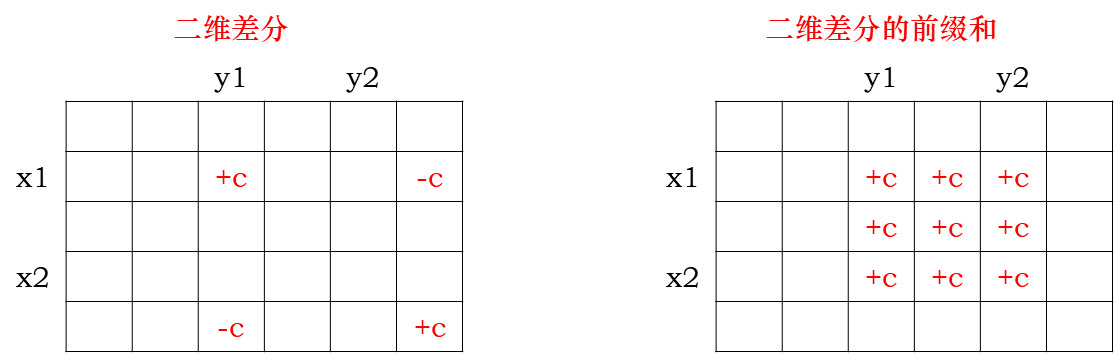
假设要把以(x1, y1)为左上角，以（x2, y2)为右下角的子矩阵加c，可以这样操作：

c[_x1][_y1]++;
c[_x1][_y2 + 1]--;
c[_x2 + 1][_y1]--;
c[_x2 + 1][_y2 + 1]++;

#include <bits/stdc++.h>
using namespace std;

int c[3005][3005];


int main() {
	memset(c, 0, sizeof (c));
	int n, m;
	cin >> n >> m;
	while (m--) {
		int _x1, _y1, _x2, _y2;
		cin >> _x1 >> _y1 >> _x2 >> _y2;
		c[_x1][_y1]++;
		c[_x1][_y2 + 1]--;
		c[_x2 + 1][_y1]--;
		c[_x2 + 1][_y2 + 1]++;
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (j != 1)
				cout << " ";
			c[i][j] = c[i - 1][j] + c[i][j - 1] - c[i - 1][j - 1] + c[i][j];
			cout << c[i][j];
		}
		cout << endl;
	}
	return 0;
}