1 背景
在日常工作中,不管是在感知或者规控,或者其它的模块中,经常需要处理两个向量之间的关系,这就引入了本篇博客和读者朋友们讨论的一个话题:Project和Product。

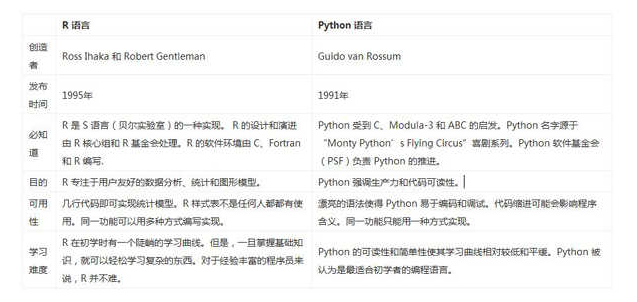
2 Project和Product
向量间的Project和Product在定义和应用上存在明显的区别,分别从定义和应用两个方面给读者朋友们作相关解释。
2.1 定义
- 投影
Project,即投影,涉及向量在某个方向上的分量计算。简单来说,一个向量在某个方向上的投影,等于该向量在该方向上的长度乘以该方向的单位向量。投影是向量分析中的一个重要概念,它有助于我们理解向量在特定方向上的表现。
如果 和
是单位向量,则投影的计算公式为:
- 点积
Product,特别是点积(Dot product),是两个向量之间的一种运算。点积的结果是一个标量,表示两个向量的相似程度或夹角。具体来说,两个向量的点积等于它们的模的乘积再乘以它们夹角的余弦值。点积在向量运算、物理和工程等领域中有广泛的应用,如计算力在某一方向上的分量、判断两向量的方向关系等。
对于两个向量 和
,它们的点积定义为:
总结来说,Project主要关注向量在特定方向上的分量,而Product(特别是点积)则关注两个向量之间的相似程度或夹角。这两者在向量分析中各有其独特的应用和价值。
2.2 应用举例
- 代码示范
在C++中,`Project`和`Product`这两个术语通常与向量和矩阵运算相关。通常会在基础的common库中自定义Project和Product的实现:
(1)点积(Dot Product)
在C++中,可以使用标准库中的算法来计算点积,例如使用 `std::inner_product`。
#include <iostream>
#include <numeric> // 包含内积算法
int main() {
double a[] = {1, 2, 3};
double b[] = {4, 5, 6};
double product = std::inner_product(a, a + 3, b, 0.0);
std::cout << "Dot product: " << product << std::endl; // 输出点积结果
return 0;
}(2)投影(Projection)
#include <iostream>
#include <numeric>
#include <cmath> // pow函数
// 向量a的归一化
double normalizeVector(double a[], size_t size) {
double norm = std::inner_product(a, a + size, a, 0.0);
for (size_t i = 0; i < size; ++i) {
a[i] /= std::sqrt(norm);
}
return norm; // 返回原始向量的范数
}
// 向量b在向量a上的投影
template<size_t N>
double project(const double a[], const double b[]) {
double proj = std::inner_product(a, a + N, a, 0.0) * std::inner_product(a, a + N, b, 0.0);
for (size_t i = 0; i < N; ++i) {
a[i] *= proj;
}
return proj;
}
int main() {
double a[] = {1, 2, 3};
double b[] = {4, 5, 6};
normalizeVector(a, 3); // 归一化向量a
project<3>(a, b); // 投影
std::cout << "Projection of b onto a: ";
for (int i : a) std::cout << i << " ";
return 0;
}