普通数组
#238、除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
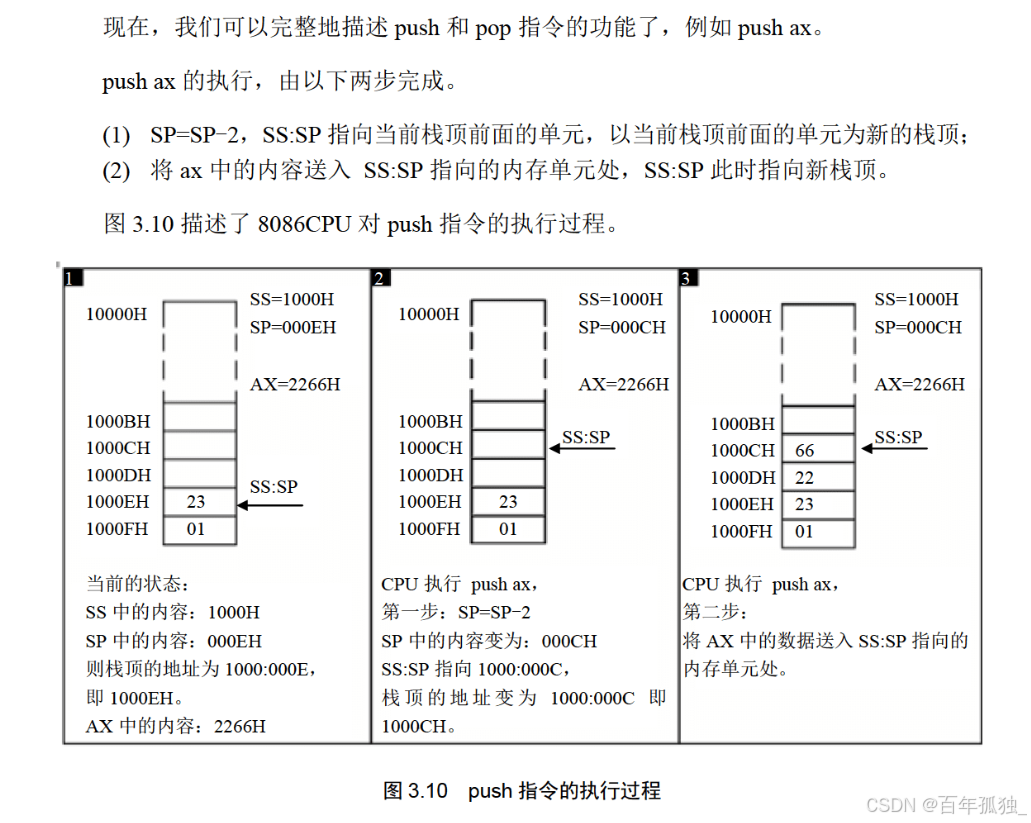
方法一:定义两个数组分别定义i左边的乘积和右边的乘积
class Solution {
//定义两个数组分别定义i左边的乘积和右边的乘积
public int[] productExceptSelf(int[] nums) {
int len=nums.length;
int[] left=new int[len];
int[] right =new int[len];
int[] ans=new int[len];
left[0]=1;//0左边没有元素,定义为1
for(int i=1;i<len;i++)
{
//i左边的乘积等于i-1左边的乘积*nums[i-1]
left[i]=left[i-1]*nums[i-1];
}
right[len-1]=1;
for(int i=len-2;i>=0;i--)
{
right[i]=right[i+1]*nums[i+1];
}
//对于每个索引计算乘积
for(int i=0;i<len;i++)
{
ans[i]=left[i]*right[i];
}
return ans;
}
}
方法二:空间复杂度为O(1)的方式
由于输出数组不算在空间复杂度内,那么我们可以将 L 或 R 数组用输出数组来计算。先把输出数组当作 L 数组来计算,然后再动态构造 R 数组得到结果。让我们来看看基于这个思想的算法。
class Solution {
public int[] productExceptSelf(int[] nums) {
int length = nums.length;
int[] answer = new int[length];
// answer[i] 表示索引 i 左侧所有元素的乘积
// 因为索引为 '0' 的元素左侧没有元素, 所以 answer[0] = 1
answer[0] = 1;
for (int i = 1; i < length; i++) {
answer[i] = nums[i - 1] * answer[i - 1];
}
// R 为右侧所有元素的乘积
// 刚开始右边没有元素,所以 R = 1
int R = 1;
for (int i = length - 1; i >= 0; i--) {
// 对于索引 i,左边的乘积为 answer[i],右边的乘积为 R
answer[i] = answer[i] * R;
// R 需要包含右边所有的乘积,所以计算下一个结果时需要将当前值乘到 R 上
R *= nums[i];
}
return answer;
}
}
#41、缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
解释:范围 [1,2] 中的数字都在数组中。
示例 2:
输入:nums = [3,4,-1,1]
输出:2
解释:1 在数组中,但 2 没有。
正确的位置是指,用x-1的位置,存放x,这样就能用n数组的下标来表示1-n之间的数。
实际上,对于一个长度为 N 的数组,其中没有出现的最小正整数只能在 [1,N+1] 中。所以只需要遍历数组,只需要看在1-N之间的数是否出现,如果出现并且它的位置不正确,就和正确位置的数进行交换,然后循环。
如果元素x属于1-N,那么就把它放入正确的位置即x-1中

class Solution {
public int firstMissingPositive(int[] nums) {
int n=nums.length;
for(int i=0;i<n;i++)
{
while(nums[i]>0&&nums[i]<=n && nums[nums[i]-1]!=nums[i])
{
int temp=nums[nums[i]-1];
nums[nums[i]-1]=nums[i];
nums[i]=temp;
}
}
//遍历完之后,只要是在1-n之间的数,都放在了正确的位置,然后遍历数组,输出第一个不正确的位置。
for(int i=0;i<n;i++)
{
if(nums[i]!=i+1)
return i+1;
}
return n+1;
}
}
#56、合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
class Solution {
public int[][] merge(int[][] intervals) {
List<int[]> result=new LinkedList<>();
Arrays.sort(intervals,(a,b)->{
return a[0]-b[0];
});
result.add(intervals[0]);
for(int i=1;i<intervals.length;i++)
{
if(intervals[i][0]>intervals[i-1][1])
{
//和前一个数组不重叠
result.add(intervals[i]);
}
//重叠,进行合并,合并后的数组为intervals[i]
else
{
intervals[i][1]=Math.max(intervals[i-1][1],intervals[i][1]);
intervals[i][0]=intervals[i-1][0];
//移除前一个数组
result.removeLast();
result.add(intervals[i]); //把intervals放入结果中,后面的与它继续比较
}
}
return result.toArray(new int[result.size()][]);
}
}
#239、滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
和单调栈一样,使用一个双端队列模拟单调队列。
class Solution {
//单调队列,维护一个单调递减队列,队头维护的是最大值
public int[] maxSlidingWindow(int[] nums, int k) {
int n=nums.length;
Deque<Integer> duque=new LinkedList<>();
int[] ans = new int[n-k+1];
for(int i=0;i<k;i++)
{
//右边的元素如果大于左边的,那么就可以把左边的元素除去
while(!duque.isEmpty()&& nums[i]>duque.peekLast())
{
duque.pollLast();
}
duque.offerLast(nums[i]);
}
ans[0]=duque.peekFirst();
for(int i=k;i<n;i++)
{
while(!duque.isEmpty()&&nums[i]>duque.peekLast())
{
duque.pollLast();
}
duque.offerLast(nums[i]);
//左窗口移动,如果移动出去的是最大值,则把最大值出队
if(duque.peekFirst()==nums[i-k])
duque.pollFirst();
ans[i-k+1]=duque.peekFirst();
}
return ans;
}
}