前言:
1.交替出场(alter) :10
2.翻翻转转(filp):0
3.方格取数(square):0
4.圆圆中的方方(round):0
总结一下: 第一次考,没爆零就是胜利,下次注意一些小错误,争取AC第一题。目标50,先立个flag(本人菜的离谱)
1.交替出场
题意:
给你一个只包含01的字符串,求这个字符串中所有01交替字串的个数(单个字符也算)
考试回顾:
想出O(n^3)的暴力枚举,但没敢用,写了个半对不对的dp,得了10分。最后老师讲O(n^3)也能过(破防),总体花的时间太长了,没达到AC。
题解:
用dp枚举左端点,一位一位向右拓展。右端点最终是几,就有几个以ta结尾的子串。最后累加即可。
AC:
const int N = 1010;
int n, ans;
char s[N];
void main() {
scanf("%s", s + 1), n = strlen(s + 1);
for (int i = 1; i <= n; i++) {
ans++;
for(j, i + 1, n) if (s[j] + s[j - 1] == '0' + '1') ans++;
else break;
}
write(ans);
}2.翻翻转转
题意:
子串si是si-1逐位取反后拼接在si-1之后的子串,现在s1为1,求s14514的第x个字符是什么。
考试回顾:
使用递归暴力,最后时间超限。(这我除了暴力想不出其他方法来了)
题解:
序列的构成非常有规律,前一半和后一半是互反的,可以考虑分治:如果答案处在前半段,继续递归下去,如果答案处在后半段,通过递归上来的答案取反后再上传即可。
AC:
#include<iostream>
#include<iomanip>
#include<cmath>
#include<string>
#include<algorithm>
#include<cstdio>
#include<queue>
#include<map>
#include<stack>
using namespace std;
int T,n;
int solve(int L,int R,int p){
if(L==R) return p;
int mid=L+R>>1;
if(n<=mid) return solve(L,mid,p);
return solve(mid+1,R,p^1);//取反
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d",&n);
printf("%d\n",solve(1,1<<30,1));
}
return 0;
}3.方格取数
题意:
你从(1,1)出发,目标是(n,m),只能向右或向下走,走过一个格子累加那个格子里的数,但不能一次性往一个方向走大于等于k步(矩阵里不能有超过k个连续的格子),求累加的最大值。如果无解输出"No Answer!"。
考试回顾:
当时没想到dp,做了个矩阵dfs,没写完。(无解的特判输出能得30!悔不当初啊)
题解:
dp,搜索记忆化。求的是走过点的权值和,考虑限制,在状态转移时,需要有:当前坐标、 步数限制、走的方向。如果走到不同方向,那么 步限制清空(注意,这里要赋值为2)然后走到新点。
AC:
#include<iostream>
#include<iomanip>
#include<cmath>
#include<string>
#include<algorithm>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<stack>
using namespace std;
const int N=201;
int n,m,k,a[N][N];
int dx[]={0,1},dy[]={1,0};
pair<int,bool> f[N][N][N][2];
int dfs(int x,int y,int step,int d){//dfs搜索记忆化
if(x>n||y>m||step>k) return -0x3f3f3f3f;
if(x==n&&y==m) return a[x][y];
if(f[x][y][step][d].second) return f[x][y][step][d].first;
f[x][y][step][d].second=1;
int ans=-0x3f3f3f3f;
if(step<k) ans=max(ans,dfs(x+dx[d],y+dy[d],step+1,d));//走和上一次相同的方向
ans=max(ans,dfs(x+dx[d^1],y+dy[d^1],2,d^1));//取反,往和上一次不同的方向走
if(ans<-1e9) return f[x][y][step][d].first=-0x3f3f3f3f;
return f[x][y][step][d].first=ans+a[x][y];
}
int main(){
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
}
}
int tmp=max(dfs(1,2,2,0),dfs(2,1,2,1));//求最大值
if(tmp>-1e9) printf("%d",tmp+a[1][1]);
else printf("No Answer!");
return 0;
}4.圆圆中的方方
题意:
求一个四个边界点为(0,0),(n,0),(0,m),(n,m)的矩形与以A为圆心,r为半径的圆的重叠部分的面积。
考试回顾:
一看解析几何,(这我怎么做?)就放弃了。但是这道题输出样例是可以骗到分的(下次不要轻易弃题了)。
题解:
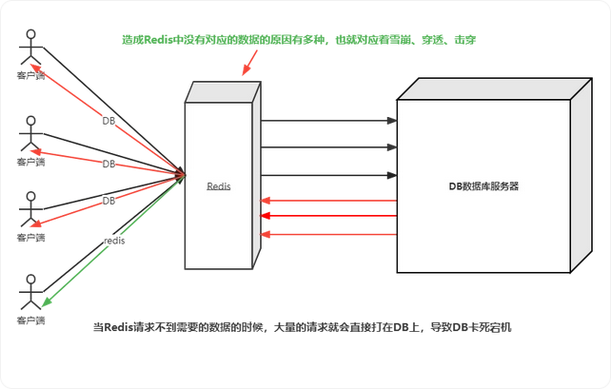
将相交的部分分成四个部分(见下图),几个部分公式如下:
1. return 0.25*pi*r*r;
2.sqrt(r*r-m*m)*m*0.5+0.5*r*r*(0.5*pi-acos(m/r)
3.sqrt(r*r-m*m)*m*0.5+sqrt(r*r-n*n)*n*0.5+0.5*r*r*(0.5*pi-acos(m/r)-acos(n/r))
4.n*m
AC:
#include<iostream>
#include<iomanip>
#include<cmath>
#include<string>
#include<algorithm>
#include<cstdio>
#include<queue>
#include<map>
#include<stack>
using namespace std;
const double pi=acos(-1),eps=1e-8;
double n,m,a,b,r;
double cal(double n,double m,double r){
if(n<m) swap(n,m);
if(n<=eps||m<=eps) return 0;
if(r<=m) return 0.25*pi*r*r;
if(r>=sqrt(n*n+m*m)) return n*m;
if(r<=n) return sqrt(r*r-m*m)*m*0.5+0.5*r*r*(0.5*pi-acos(m/r));
return sqrt(r*r-m*m)*m*0.5+sqrt(r*r-n*n)*n*0.5+0.5*r*r*(0.5*pi-acos(m/r)-acos(n/r));
}
int main(){
cin>>n>>m>>a>>b>>r;
printf("%lf",cal(a,b,r)+cal(n-a,b,r)+cal(a,m-b,r)+cal(n-a,m-b,r));
return 0;
}见下图: