给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
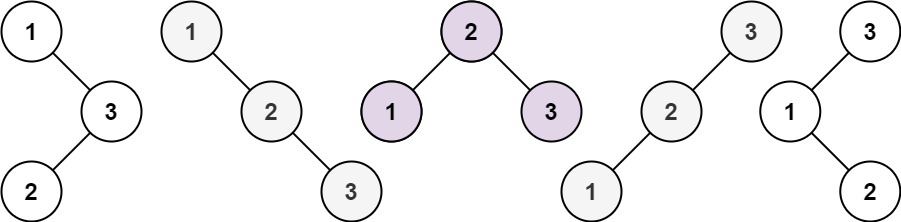
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1, 0); // 动态规划数组 dp,表示 i 个节点可以组成的二叉搜索树的数量
dp[0] = 1; // 0 个节点时只有一种情况(空树)
dp[1] = 1; // 1 个节点时也只有一种情况(只有根节点的树)
for (int i = 2; i <= n; ++i) { // 从 2 个节点开始逐步计算 dp[i]
for (int j = 1; j <= i; ++j) {
dp[i] += dp[j - 1] * dp[i - j]; // dp[j-1] 是左子树的可能数,dp[i-j] 是右子树的可能数
}
}
return dp[n];
}
};
二叉搜索树(BST)的性质:
- 每个节点的左子树的所有节点值都小于根节点。
- 每个节点的右子树的所有节点值都大于根节点。
举例说明:
当 n=4时,所有可能的根节点分别是 1、2、3、4。
-
选择 1 为根节点:
- 左子树有 0 个节点:
dp[0] = 1 - 右子树有 3 个节点:
dp[3] = 5 - 此时组合数为:
1 * 5 = 5
- 左子树有 0 个节点:
-
选择 2 为根节点:
- 左子树有 1 个节点:
dp[1] = 1 - 右子树有 2 个节点:
dp[2] = 2 - 此时组合数为:
1 * 2 = 2
- 左子树有 1 个节点:
-
选择 3 为根节点:
- 左子树有 2 个节点:
dp[2] = 2 - 右子树有 1 个节点:
dp[1] = 1 - 此时组合数为:
2 * 1 = 2
- 左子树有 2 个节点:
-
选择 4 为根节点:
- 左子树有 3 个节点:
dp[3] = 5 - 右子树有 0 个节点:
dp[0] = 1 - 此时组合数为:
5 * 1 = 5
- 左子树有 3 个节点:
因此,dp[4] = 5 + 2 + 2 + 5 = 14。