LORA DASH -一种更高效的微调方式

news2024/11/20 4:17:04

概述

大型语言模型（LLMs）通过在大规模数据集上的预训练，能够捕捉和学习丰富的语言特征和模式。目前，尽管预训练模型在诸多任务上取得了显著的成果，但它们在特定任务上的表现仍有提升空间。为了进一步提升模型的性能，研究者们通常采用微调（Fine-tuning）的方法，即在预训练的基础上，针对特定任务继续训练模型。微调过程虽然有效，但也带来了显著的资源消耗问题。尤其是对于包含数十亿甚至数千亿参数的大型模型，全参数微调需要巨大的计算资源和内存消耗。为了解决这一问题，研究者们提出了参数高效微调（Parameter Efficient Fine-Tuning, PEFT）策略，旨在通过调整模型中的一部分参数来实现对特定任务的优化，从而减少计算和内存成本。在众多PEFT方法中，LoRA（Low-Rank Adaptation）因其在保持模型性能的同时减少参数调整量而受到广泛关注。LoRA通过在模型的权重矩阵中引入低秩结构来模拟权重的变化，从而实现参数效率。尽管LoRA在实践中取得了一定的成功，但其在理解和利用所谓的“任务特定方向”（Task-Specific Directions, TSD）方面存在不足。

任务特定方向是指在预训练阶段未被充分强调，但在特定下游任务中至关重要的权重方向。这些方向在微调过程中的调整对于提升模型在特定任务上的性能至关重要。然而，现有研究在定义和利用TSD方面存在模糊和不一致之处，这限制了LoRA及其他PEFT方法的性能潜力。

为了解决这一问题，一项研究提出了一种新的PEFT方法——LoRA-Dash。LoRA-Dash旨在通过更精确地定义和利用TSD，进一步释放PEFT的潜力。通过构建一个清晰的TSD框架，LoRA-Dash能够在微调过程中更有效地捕捉和利用任务特定方向，从而提升模型在特定任务上的性能。

Lora回顾

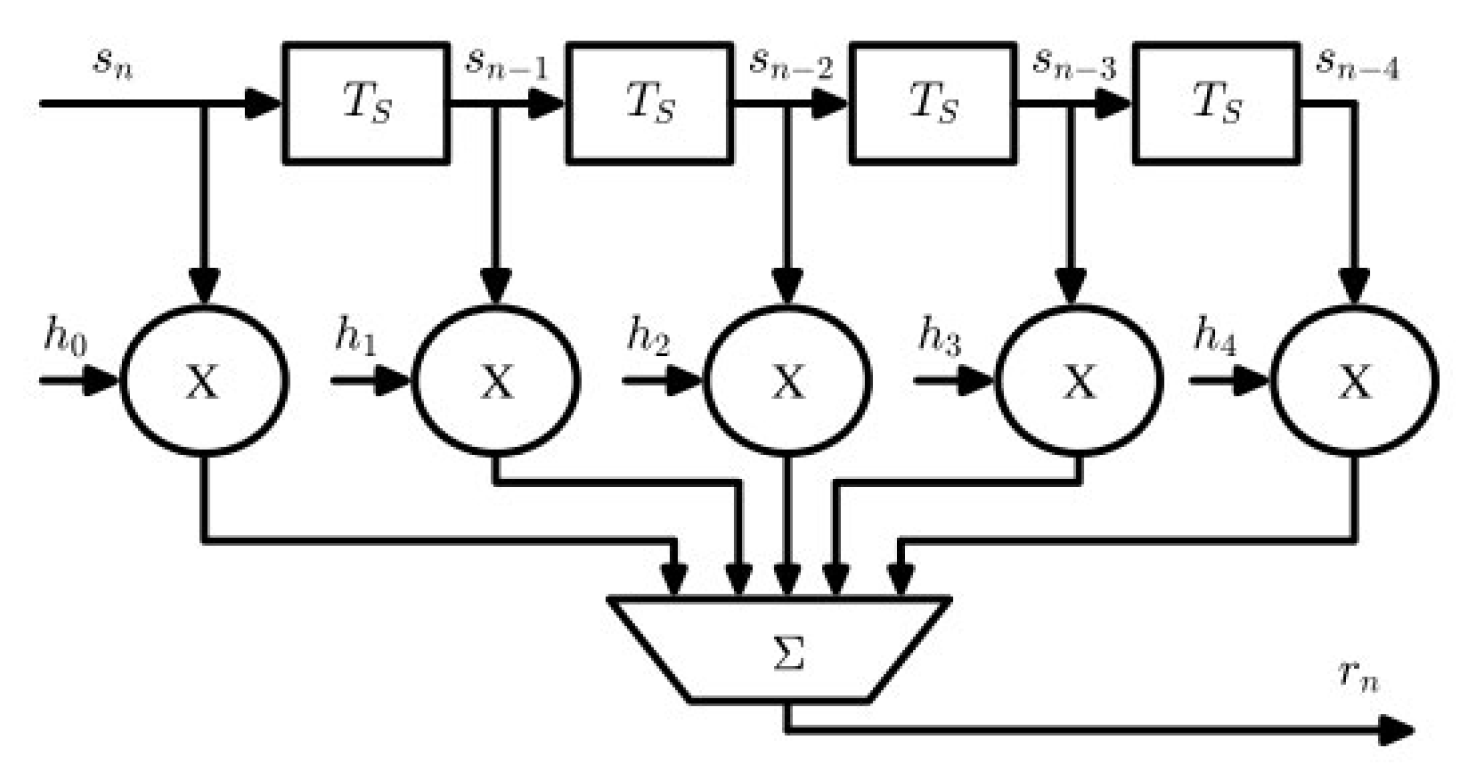
传统LoRA的核心思想是通过对模型权重矩阵的低秩分解来实现参数的高效更新。具体来说，对于模型中某个权重矩阵 $\in \mathbb{R}^{n \times m}$ ，LoRA通过两个低秩矩阵 $\in \mathbb{R}^{n \times r}, \quad B \in \mathbb{R}^{r \times m} \quad \text{(where $ r \ll \{n, m\}) $}$ 来近似权重矩阵的更新 $\Delta W$ ，即： $\Delta W \approx AB$
在这里插入图片描述

在训练过程中，只有( A )和( B )会被更新，而原始的权重矩阵( W )保持不变。这样，通过仅更新少量参数，就能实现对模型的微调。这样做相比于其他参数微调主要有以下几个优点：

参数效率：LoRA通过低秩矩阵更新权重，大幅减少了需要训练的参数数量。
计算资源节省：由于参数数量的减少，LoRA在微调过程中显著降低了计算资源和内存的消耗。
灵活性：LoRA可以很容易地应用于不同的模型和任务，具有很好的通用性。

但是同时也有缺点：

效果限制：尽管LoRA减少了参数数量，但这种近似方法可能限制了模型性能的提升。
方向选择问题：LoRA在初始化和更新( A )和( B )时，并没有明确的方向指导，这可能导致微调效果不如预期。
缺乏任务特定优化：LoRA虽然参数高效，但缺乏对特定任务优化的机制，可能无法充分发挥模型在特定任务上的潜力。

本文中提到的LoRA-Dash是一种基于LoRA的新方法，旨在解决LoRA在方向选择和任务特定优化方面的不足。总的来说，LoRA-Dash在LoRA的基础上，通过引入任务特定方向的概念和两个阶段的微调策略，实现了对模型更精确和高效的微调，有望在各种下游任务中取得更好的性能。

概念框架定义：LoRA-Dash的关键概念与数学表示

LoRA-Dash方法在LoRA的基础上引入了一系列新的概念，以更精确地定义和利用任务特定方向（Task-Specific Directions, TSD）。以下是LoRA-Dash中关键概念的定义及其数学表示：

1. 矩阵的基与方向

定义 1（矩阵的基）： 对于一个矩阵 $\ A \in \mathbb{R}^{n \times m}$ ，其左奇异向量和右奇异向量分别由矩阵 ( U ) 和 ( V ) 表示，矩阵 ( A ) 的基定义如下：

核心基： 矩阵 ( A ) 的核心基定义为 ${u_i v_i^T\} )$ ，其中每个 $u_i v_i^T )$ 是由奇异向量 $u_i )$ 和 $v_i )$ 构成的秩为 1 的矩阵。
全局基： 矩阵 ( A ) 的全局基定义为 ${u_i v_j^T\} )$ 对于所有 $(i, j)$ ，涵盖了左奇异向量和右奇异向量的所有组合。

定义 2（矩阵的方向）： 矩阵 $(A)$ （其中 $(n < m)$ 的方向基于其全局基定义，采用其奇异值 $\Sigma )$ 的扩展集合，并用零填充，具体表示为 $(\sigma_1, 0, \ldots, 0, \sigma_2, 0, \ldots, 0, \ldots, \sigma_n, \ldots, 0) \in \mathbb{R}^{nm} )$ ，即通过行展平的 $\Sigma )$ 。

2. 任务特定方向（TSD）

定义 3（任务特定方向）： 对于某个特定任务和预训练权重矩阵 $(W)$ ，假设该任务的最优权重为 $W^* )$ ，则该任务在 ( W ) 上的任务特定方向（TSD）是指那些在从 $(W)$ 到 $W^* )$ 的变化过程中，其坐标值表现出显著高变化率 $\delta )$ 的核心方向。
数学表示：
$\delta_i = \left| \frac{u_i^T \Delta W v_i}{\sigma_i + \epsilon} \right| ]$
其中， $u_i )$ , $v_i )$ , 和 $\sigma_i )$ 分别是 ( W ) 的第 ( i ) 个左奇异向量、右奇异向量和奇异值， $\Delta W )$ 是 $(W)$ 的变化量， $\epsilon )$ 是一个常数，防止奇异值为零。

3. LoRA-Dash的两个阶段

LoRA-Dash包含两个主要阶段：

预启动阶段： 在此阶段，通过训练矩阵 ( A ) 和 ( B ) 来捕捉任务特定方向（TSD）的信息。
冲刺阶段： 在此阶段，利用识别出的TSD进行更有针对性的微调，以加速模型在新任务中的适应性调整。

尽管LoRA-Dash在定义和利用TSD方面取得了进展，但在实际应用中，由于 $\Delta W^* )$ 和 $W^* )$ 在微调前是未知的，这使得提前利用TSD信息变得具有挑战性。LoRA-Dash通过在预启动阶段识别TSD，并在冲刺阶段有针对性地利用这些方向，有效地克服了这些挑战，从而在各种下游任务中实现了显著的性能提升。