2.5 有限冲激响应（FIR）滤波器

在此阶段，我们知道，大多数实际感兴趣的信号可以看作是不同频率下振荡的复数正弦波的总和。这些正弦波的幅度和相位决定了该信号的频率内容，分别通过幅度响应和相位响应表示。在数字信号处理（DSP）中，设计的目标是以预定的方式修改输入信号的频率内容，以获得所需的输出。这种操作称为滤波（filtering） ，它是整个DSP领域中最基本的操作。

可以设计一个系统或滤波器，使信号中的某些期望的频率内容通过该系统，方法是对这些频率的 $\approx 1$ 进行指定，而其他频率内容可以通过对 $\approx 0$ 进行指定来抑制（尽管这个想法是正确的，但正如我们将很快看到的，这并不是一项简单的任务）。这个概念类似于一个水过滤器，它处理水中的杂质，以及一个油过滤器，它去除发动机油中的污染物。术语低通、高通和带通则表示的是对需要通过的频谱内容的直观感知，其中低、高手以及带通分别表示需要通过的频谱内容，同时阻止其余的内容。

滤波器频率响应

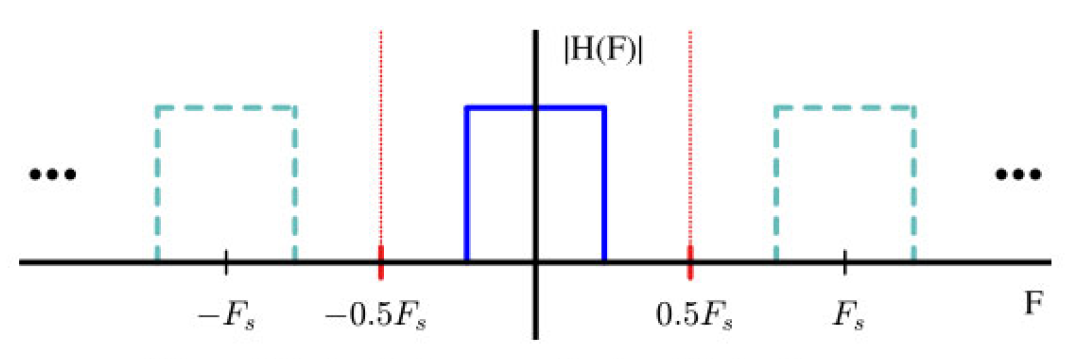
图2.15：理想的低通滤波器具有砖墙响应

图2.15显示了理想低通滤波器的幅度响应 $∣ H (F) ∣$ （作为连续频率的函数）。低通滤波器通过接近0的频率，同时阻挡其余频率。在连续频率的世界中，只有中间的滤波器存在。然而，在采样的世界中，滤波器的频率响应——就像采样信号一样——以采样频率 $F_s$ 的间隔重复，且两侧存在无限个频谱副本，如图2.15中的虚线所示。采样频率响应的基带范围是从 $0.5F_s$ 到 $0.5F_s$ ，在红色虚线内显示。

另一方面，高通滤波器通过正频率和负频率接近 $±0.5Fs \pm 0.5F_s$ 的频率，同时阻止其他所有频率，这可以通过 $0.5F_s$ 附近的对称性观察到。

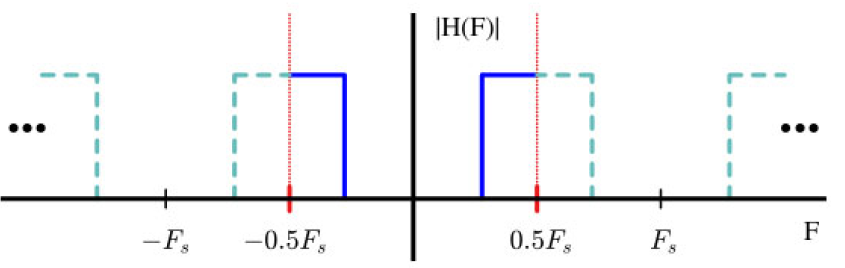
图2.16：理想的高通滤波器

类似地，带通滤波器只允许频谱中这两个极端之间的特定部分通过。

FIR滤波器设计

由于滤波器是修改信号频谱内容的系统，因此它自然也具有脉冲响应。当这种脉冲响应的长度是有限的时，这种滤波器称为有限冲激响应（FIR）滤波器，它是离散时间序列，其样本称为滤波器系数。

我们可以通过简单地计算理想频率响应 $H (F)$ 的逆变换来完成这一任务。由于理想滤波器具有统一的通带和零阻带，并且两者之间有直接的过渡（类似于矩形信号），这种有限频域支持会产生无限的脉冲响应，因此是不可实现的。为什么？因为矩形信号在连续频域中的逆变换是时间域中具有无限支持的正弦信号。

假设这种逆变换仍然获得并采样以生成离散时间信号 $h [n]$ 。当它在两侧被截断时，相当于将理想的无限信号 $h [n]$ 乘以一个矩形窗 $w_{\text{Rect}}[n]$ ，公式如下：

$h_{\text{Truncated}}[n] = h[n] \cdot w_{\text{Rect}}[n]$

如前所述，加窗（windowing） 是将无限序列修剪为有限长度的过程。我们知道时间域中的相乘相当于频率域中的卷积，而时间域矩形窗的频谱是sinc信号。因此，理想滤波器的频谱与该sinc信号的频谱卷积产生滤波器的实际频率响应 $H (F)$ ：

$\text{理想砖墙响应} \cdot \text{sinc}(F)$

如图2.17所示。该频域的sinc信号具有主瓣，并且从 $-\infty$ 延伸到 $\infty$ 的衰减振荡。

这些衰减振荡的卷积是实现FIR滤波器在通带和阻带中始终表现出波纹的原因。
当sinc信号的主瓣与砖墙频谱卷积时，它在通带和阻带之间生成过渡带。自然，这个过渡带的带宽等于sinc主瓣的宽度，反过来又取决于时间域中矩形窗的长度。

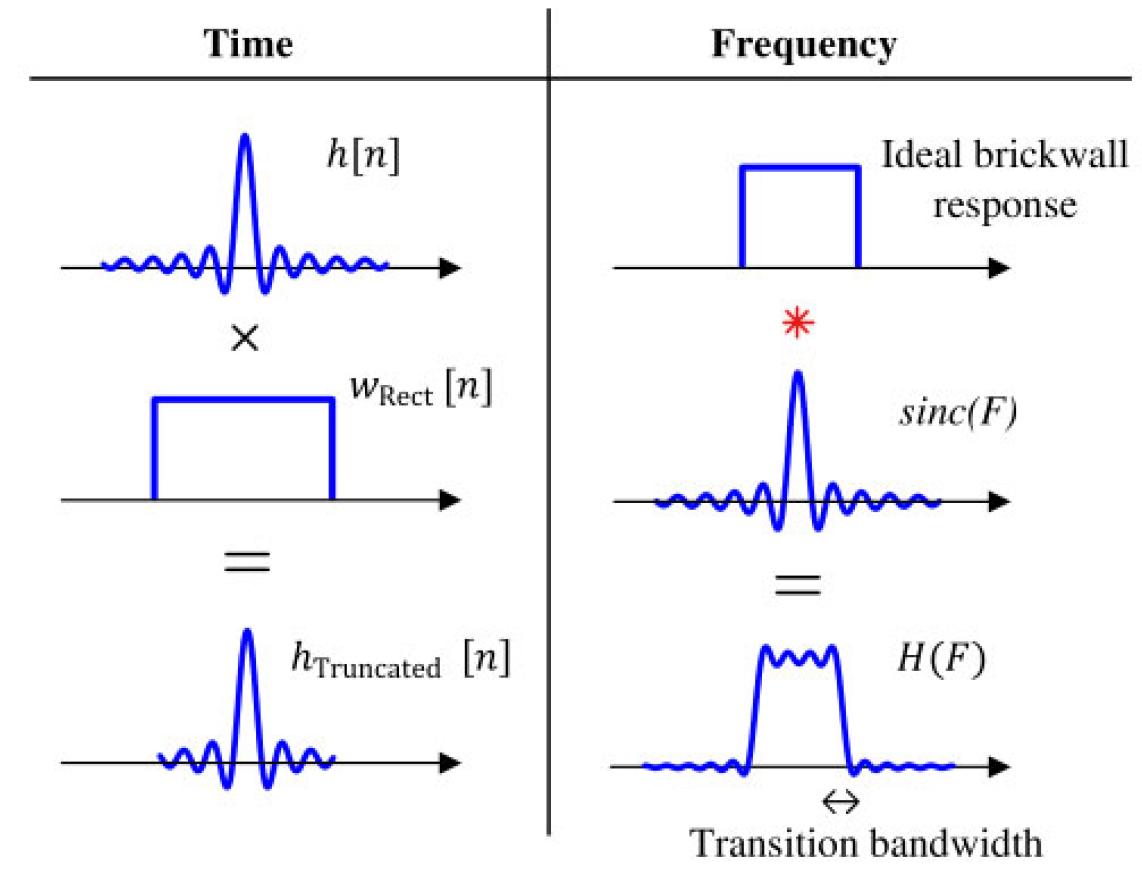
图2.17：时间域中脉冲响应截断过程及其在频率域中的影响。

最终，通过窗口进行截断使FIR滤波器具有有限时长的脉冲响应 $h [n]$ 。

左侧时间域部分：

$h [n]$ 是理想的无限冲激响应信号。
当它与矩形窗 $w_{\text{Rect}}[n]$ 相乘时，得到了截断的信号 $h_{\text{Truncated}}[n]$ ，即截断后的有限脉冲响应。

右侧频率域部分：

理想砖墙频率响应与 sinc 函数频谱（通过窗口截断）卷积后，生成实际频率响应 $H (F)$ 。
此外，卷积会引入衰减波纹和过渡带宽度（如图所示）。

滤波器阻带中出现的旁瓣、过渡带的带宽和通带中的波纹特性表征了滤波器的性能。通常以分贝（dB） 为单位表示这些参数。滤波器的dB值公式如下：

$[H(F)]_{\text{dB}} = 20\log_{10}|H(F)|$

应记住，上述公式中的乘法因子20在电压或电流平方等功率转换中被替换为10。将幅度转换为dB值的优点在于它便于绘制小到极大的数量值，从而在一张图中清晰显示。

根据表2.2中的参数设计滤波器，并在图2.18中以图形方式展示。

FIR滤波器设计的基本任务是找到滤波抽头（或系数） 的值，这些值可以转换为所需的频率响应。为此，许多软件工具可用。一种标准的FIR滤波器设计方法是Parks-McClellan算法。该算法是一个迭代算法，用于找到最优的FIR滤波器，使得期望频率响应与实际频率响应之间的最大误差最小化。

使用该算法设计的滤波器具有在其频率响应中的等波纹行为，有时称为等波纹滤波器。等波纹一词意味着通带和阻带内的波纹相等，但不一定在两个带内都相等。

表2.2：滤波器规范参数

参数符号	参数说明
$F_S$	采样率（Sample rate）
$F_{\text{pass}}$	通带边缘频率（Passband edge frequency）
$F_{\text{stop}}$	阻带边缘频率（Stopband edge frequency）
$\delta_{\text{pass}}$	最大通带波动（Maximum passband ripple）
$\delta_{\text{stop}}$	最大阻带波动（Maximum stopband ripple

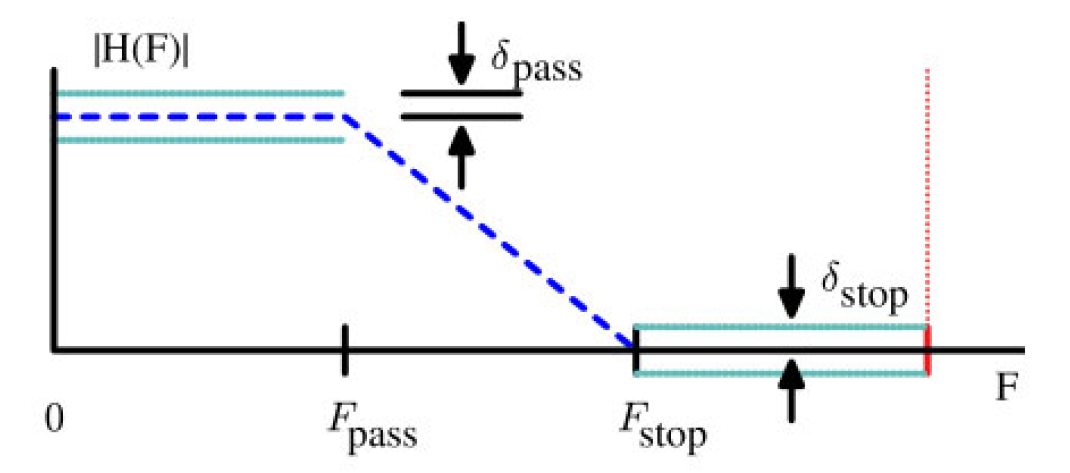
图2.18：采样低通滤波器的参数规范

示例 2.3

我们通过Parks-McClellan算法在Matlab中设计了一个低通FIR滤波器，满足以下规格：

采样率 $F_S = 12 \, \text{kHz}$
通带边缘频率 $F_{pass} = 2 \, \text{kHz}$
阻带边缘频率 $F_{stop} = 3 \, \text{kHz}$
通带波动 $\delta_{pass, dB} = 0.1 \, \text{dB}$
阻带波动 $\delta_{stop, dB} = -60 \, \text{dB}$

首先，从图2.18中可以看出，频域通带的最大幅度为 $\delta_{pass}$ ，我们可以将dB单位转换为线性单位，具体如下：

$\log_{10} (1 + \delta_{pass}) = \delta_{pass,dB}$

$\delta_{pass} = 10^{\delta_{pass,dB}/20}$

$\delta_{pass} = 0.012$

对于阻带：

$\log_{10} \delta_{stop} = \delta_{stop,dB}$

$\delta_{stop} = 10^{-60/20}$

$\delta_{stop} = 0.001$

Matlab函数firpm()返回长度为** $N + 1$ 的线性相位FIR滤波器的系数。对于一个试验值 $N = 29$ ** ：

$\ F_{\text{pass}} \ F_{\text{stop}} \ 0.5F_s]/(0.5F_s), [1 \ 1 \ 0 \ 0])$

$\ 2000 \ 3000 \ 6000]/6000, [1 \ 1 \ 0 \ 0])$

其中，向量 $\ 1 \ 0 \ 0]$ 指定了通过带通和阻带边缘的目标振幅。0.5 $F_s$ 的归一化并无实际意义，它只是Matlab函数的一个要求。此外，滤波器的设计使用了Matlab提供的 $N + 1$ 系数，这就是我们在参数中使用 $N - 1$ 的原因。

如果你试试这个简单的代码，你会发现获得的结果具有约-45 dB的阻带水平和0.05 dB的通带波纹。 边带并没有满足60 dB的衰减，而通带波纹超过了0.1 dB的要求。因此，可以增加 $N$ 值，直到达到60 dB的衰减，约为 $N = 41$ 。为了避免滤波器长度过大增加处理器的工作负荷，也可以采用不同的权重因子来调节通带和阻带波纹。举例来说，通带到阻带的1:10的权重因子（在向量形式中为 $\ 10$ ）可得到：

$\ 2000 \ 3000 \ 6000]/6000, [1 \ 1 \ 0 \ 0], [1 \ 10])$

在这种情况下，边带水平达到了-55 dB，相比于没有权重时** $N = 29$ 时的-45 dB提高了10 dB。** 接下来，滤波器的阶数逐步增加，直到达到期望的规格，为 $N = 33$ ，比不使用权重时减少了8个采样点。如果没有权重因子，并且使用 $N = 41$ ，这样的试验和误差方法通常是设计符合给定规格的滤波器所必需的。

最终滤波器的冲激响应** $h [n]$ 和频率响应 $20\log_{10}|H(F)|$ 如图2.19所示。** 注意到阻带衰减为60 dB，通带波纹在0.1 dB之内。

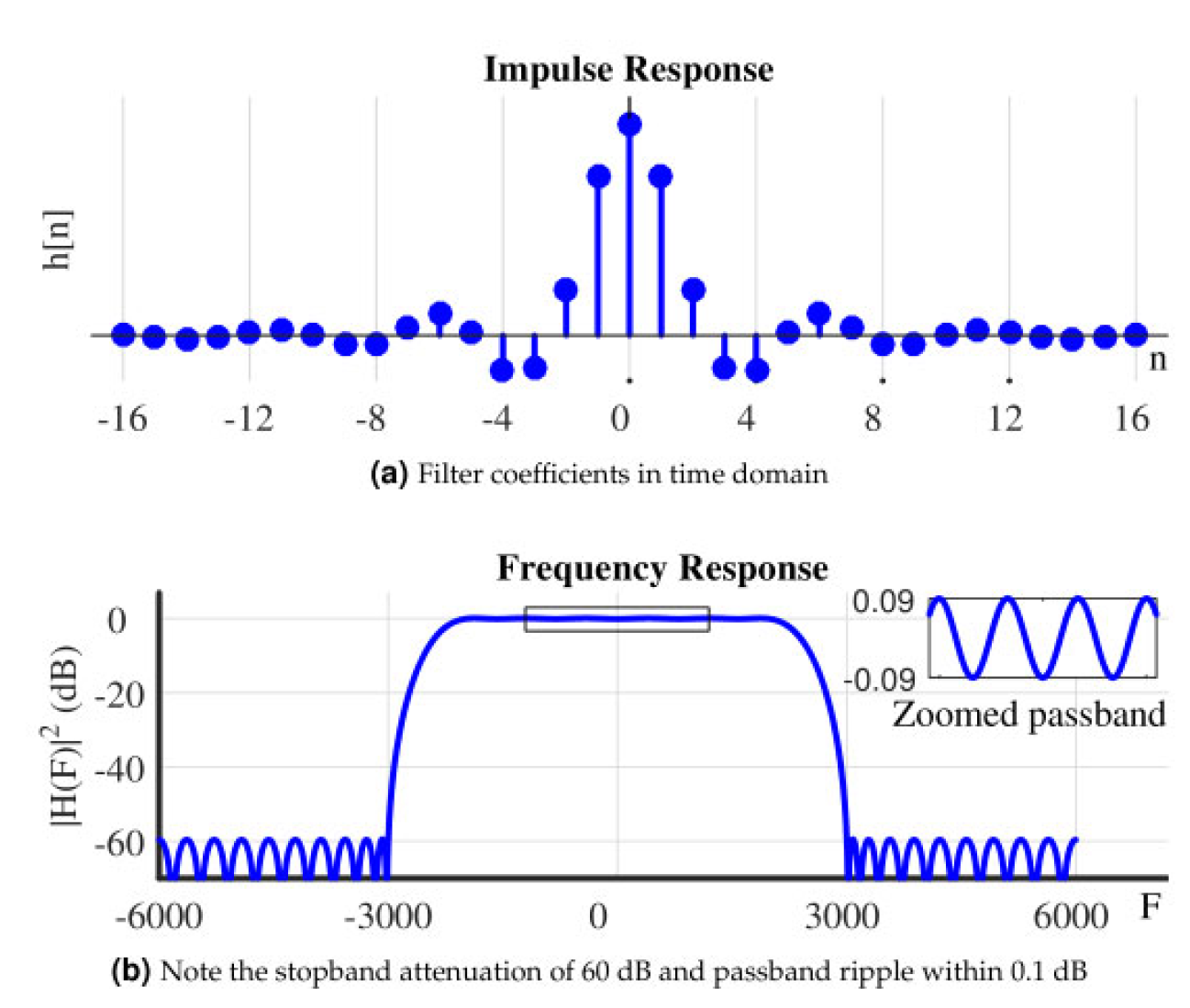
图 2.19：通过Parks-McClellan算法设计的低通FIR滤波器的时间和频率响应，滤波器阶数为 $N = 33$ 。

我们在上面的例子中学到，抽头数越多，滤波器越接近预期的响应（例如，低通、高通、带通等），但代价是计算复杂度的增加。因此，FIR滤波器的决定性特征是其系数的数量 $L_{FIR}$ 。

虽然设计的例子看似简单，但在设计滤波器时还有许多其他因素需要考虑，比如DSP平台、硬件、处理器内存、时钟速度、动态范围，以及根据Fred Harris的说法，甚至包括你配偶的生日。因此，滤波器的设计应始终从系统的角度出发，而不是将其作为系统中的一个独立组件设计。换句话说，除了对输入信号进行滤波，设计还应考虑其他几项次要任务的整合。

‍

卷积

由于具有固定系数的FIR滤波器是一个线性时不变（LTI）系统，其输出是其冲激响应 $h [n]$ 与输入信号 $s [n]$ 之间的卷积。对于长度为 $L_{FIR}$ 的FIR滤波器，

$\sum_{m=0}^{L_{FIR}-1} h[m] s[n - m] \tag{2.28}$

图 2.20 展示了一个 5 阶 FIR 滤波器。为了实现卷积，FIR 滤波器由一组乘法器、加法器和延迟元件组成。延迟元件只是一个时钟控制的寄存器用于存储输入值，并用 $T_S$ 符号表示（单个采样延迟）。

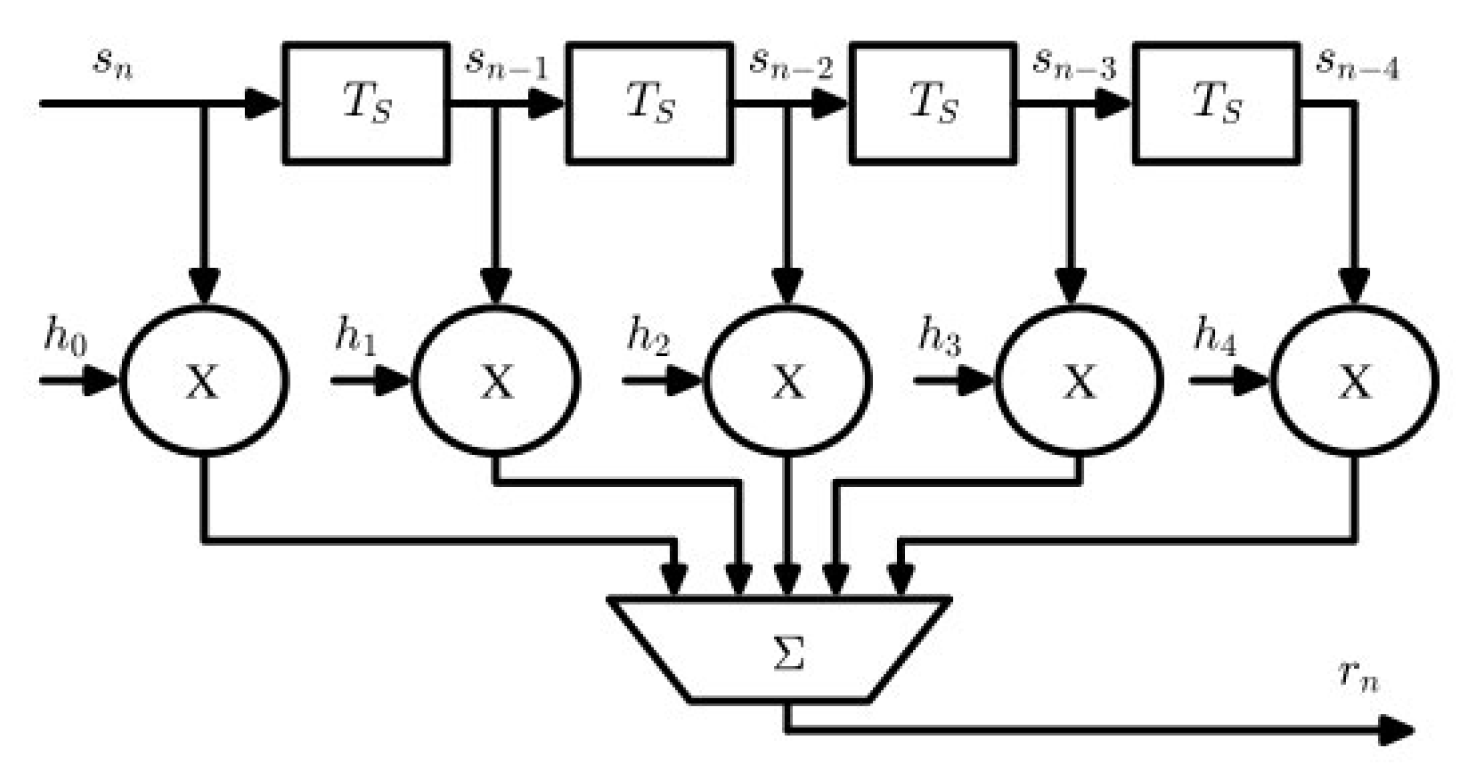
图 2.20：用具有冲激响应 $h [n]$ 的FIR滤波器对信号 $s [n]$ 进行滤波。

考虑到图 2.20 中的结构，这个 5 阶滤波器的输出可以用数学表示为：

$r [n] = h [0] s [n] + h [1] s [n - 1] + h [2] s [n - 2] + h [3] s [n - 3] + h [4] s [n - 4]$

在每个时钟周期，从输入数据和滤波器抽头中采样并进行乘法运算，所有乘法器的输出相加，形成一个输出。在下一个时钟周期，输入数据采样向右移动 1 位，以容纳一个新到达的样本，滤波器抽头相应移动，过程持续进行。

由于一系列延迟元件的存在，这种结构通常被称为抽头延迟线滤波器或横向滤波器。如果我们有一系列的双输入加法器，每个加法器的两个输入与固定系数的乘法器耦合在一起，形成一个乘累加（MAC）结构。另一种选择是转置结构，在该结构中，寄存器作为部分和累加器运行。

群延迟、线性相位和系数对称性

假设一个信号 $s [n]$ 需要进行低通滤波而不产生失真。似乎滤波器 $H [k]$ 的任务是：

去除信号带宽之外的所有频谱内容，且
在不损害信号带宽内的频谱内容的情况下通过，即滤波器的通带应尽可能平坦。

然而，在这种描述中，我们忽略了滤波器的相位响应，而相位响应也有可能损害波形形状，即使仅仅专注于滤波器的幅度响应也可能未能察觉。因此，我们可以写出滤波器 $H [k]$ 的频率响应如下：

$\begin{cases} 1 & \frac{-k_{\text{pass}}}{N} < k < \frac{k_{\text{pass}}}{N} \\ 0 & \text{其他位置} \end{cases}$

$\angle H[k] = ?$

其中， $k_{\text{pass}}/N$ 是通带频率。由于该幅度响应，该低通滤波器的输出与输入信号 $s [n]$ 是相同的。问题是：它应该有什么样的相位响应，以便在滤波操作后波形形状得以保留？

我们知道，像所有实际系统一样，滤波操作会在输入信号和输出信号之间引入延迟。回忆第1.9节，信号 $s[(n - n_0) \mod N]$ 的离散傅里叶变换 (DFT) $\hat{S}[k]$ 具有不变的幅度，而其相位则会根据每个 $k$ 旋转 $-2\pi(k/N)n_0$ 。

$|\hat{S}[k]| = |S[k]|$

$\angle \hat{S}[k] = \angle S[k] - 2\pi \frac{k}{N}n_0$

还要记住，频域中滤波器的输出是输入频谱和滤波器频谱的乘积。在复数运算中，它是幅度响应的乘积和相位响应的加法。

根据以上两个事实，我们可以推断，如果滤波器的相位响应如下所示：

$\angle H[k] = -2\pi \frac{k}{N} n_0 \tag{2.29}$

其中 $n_0$ 是某个延迟，那么输出信号将是输入信号的精确延迟版本。此处看到的相位响应是离散频率 $k / N$ 的线性函数。如果相位是非线性的，那么波形中引入的延迟与频率不成比例，因此不同的组成正弦波会因不同的时间延迟而失真，导致信号形状失真。

为了找到这个延迟 $n_0$ ，卷积后输出信号 $r [n]$ 的长度由输入信号 $s [n]$ 和脉冲响应 $h [n]$ 决定，其长度公式如下（即公式 2.8 再次给出）：

$\text{Length}\{r[n]\} = \text{Length}\{s[n]\} + \text{Length}\{h[n]\} - 1$

比输入信号长了 $\text{Length}\{h[n]\} - 1$ 个样本。假设滤波器长度是奇数，我们可以说，每个 FIR 滤波器使输出信号延迟的样本数由下式给出：

$n_0 = \frac{\text{Length}\{h[n]\} - 1}{2} \tag{2.30}$

这被称为滤波器的群延迟。在我们的应用中，它对应于中间脉冲响应的峰值（见图 2.19a），因此公式分母为 2。结果是，开始时的 $n_0$ 个样本——即滤波器正在进入输入序列时——可以被舍弃。同样，滤波器正在移出输入序列时的最后 $n_0$ 个样本也可以被舍弃。

在此上下文中，群延迟非常类似于日常生活中的许多例子，比如在充分进入状态和伸展之前的预热、启动和关闭计算机的时间，以及春秋季节过渡到实际的长冬/长夏季之前。

更精确地说，群延迟定义为相位响应相对于频率的导数的负值。另一方面，相位延迟定义为相位响应除以频率的负值。对于线性相位滤波器，群延迟和相位延迟是相同的，如公式 (2.29) 所示：

$-\frac{1}{2\pi} \frac{d\angle H(F)}{dF} = n_0 = -\frac{1}{2\pi} \frac{\angle H[k]}{k/N}$

在 FIR 滤波器中保持精确的线性相位是一项简单的任务（但在一般滤波器设计中并非如此）。假设一个长度为奇数的 FIR 滤波器具有对称系数：

系数对称意味着每个样本在时间 $n_0$ 时都有一个类似样本位于时间 $n_0$ ，因为信号是以 0 为中心的。
这两个样本是时域中的两个脉冲，它们形成了频域中的一个实数正弦波，代表没有相位的频谱幅度。

因此，唯一的相位来自于将脉冲响应的第一个样本移到时间 0 时产生的延迟。时间上的移位意味着线性相位，见公式 (1.58)。

这就是为什么你通常会看到 FIR 滤波器具有对称的脉冲响应，并且这是 FIR 滤波器在 DSP 应用中广泛使用的主要原因之一。

‍