如果 b > 0 b > 0 b>0 且 b ≠ 1 b \neq 1 b=1,则指数函数 f ( x ) = b x f(x) = b^x f(x)=bx 不是递增就是递减,因此它是通过水平线测试的单调函数。所以它具有反函数 f − 1 f^{-1} f−1,称为以 b b b 为底的对数函数,记作 log b \log_b logb。如果我们使用反函数的表达式:
f − 1 ( x ) = y ⟺ f ( y ) = x f^{-1}(x) = y \iff f(y) = x f−1(x)=y⟺f(y)=x
那么我们有:
log b x = y ⟺ b y = x (1) \log_b x = y \iff b^y = x \tag{1} logbx=y⟺by=x(1)
因此,如果 x > 0 x > 0 x>0,则 log b x \log_b x logbx 是底数 b b b 必须升到的指数以得到 x x x。
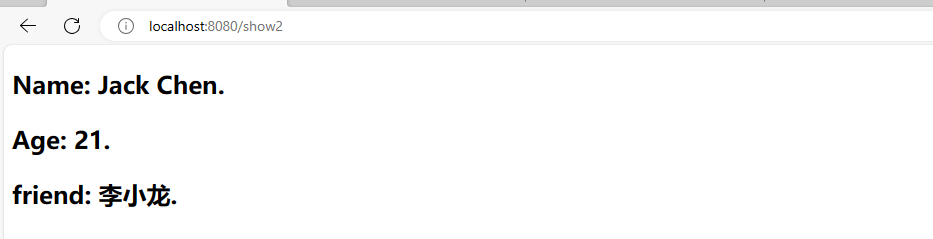
例1 求解下列对数:(a) log 3 81 \log_3 81 log381, (b) log 25 5 \log_{25} 5 log255, (c) log 10 0.001 \log_{10} 0.001 log100.001
解:
(a) log 3 81 = 4 \log_3 81 = 4 log381=4,因为 3 4 = 81 3^4 = 81 34=81
(b) log 25 5 = 1 2 \log_{25} 5 = \frac{1}{2} log255=21,因为 2 5 1 / 2 = 5 25^{1/2} = 5 251/2=5
© log 10 0.001 = − 3 \log_{10} 0.001 = -3 log100.001=−3,因为 1 0 − 3 = 0.001 10^{-3} = 0.001 10−3=0.001
消去方程应用于函数 f ( x ) = b x f(x) = b^x f(x)=bx 和 f − 1 ( x ) = log b x f^{-1}(x) = \log_b x f−1(x)=logbx 时,变为:
log b ( b x ) = x for every x ∈ R b log b x = x for every x > 0 \tag{2}\begin{align*} \log_b(b^x) &= x \quad \text{for every} \ x \in \mathbb{R}\\ b^{\log_b x} &= x \quad \text{for every} \ x > 0 \end{align*} logb(bx)blogbx=xfor every x∈R=xfor every x>0(2)
对数函数 log b \log_b logb 的定义域是 ( 0 , ∞ ) (0, \infty) (0,∞),值域是 R \mathbb{R} R,并且它是连续的,因为它是一个连续函数的反函数,即指数函数。它的图像是 y = b x y = b^x y=bx 关于直线 y = x y = x y=x 的反射。
图 1 显示了 b > 1 b > 1 b>1 的情况。(最重要的对数函数的底数 b > 1 b > 1 b>1。)事实上, y = b x y = b^x y=bx 是一个在 x > 0 x > 0 x>0 时快速增长的函数,这反映在 y = log b x y = \log_b x y=logbx 是一个在 x > 1 x > 1 x>1 时缓慢增长的函数。

图 2 显示了 y = log b x y = \log_b x y=logbx 在不同底数 b > 1 b > 1 b>1 下的图像。因为 log b 1 = 0 \log_b 1 = 0 logb1=0,所以所有对数函数的图像都经过点 ( 1 , 0 ) (1, 0) (1,0)。

以下定理总结了对数函数的性质。
定理 3 如果 b > 1 b > 1 b>1,则函数 f ( x ) = log b x f(x) = \log_b x f(x)=logbx 是一个一一对应的、连续的、递增的函数,定义域为 ( 0 , ∞ ) (0, \infty) (0,∞),值域为 R \mathbb{R} R。如果 x , y > 0 x, y > 0 x,y>0 且 r r r 是任意实数,那么:
- log b ( x y ) = log b x + log b y \log_b(xy) = \log_b x + \log_b y logb(xy)=logbx+logby
- log b ( x y ) = log b x − log b y \log_b \left( \frac{x}{y} \right) = \log_b x - \log_b y logb(yx)=logbx−logby
- log b ( x r ) = r log b x \log_b (x^r) = r \log_b x logb(xr)=rlogbx
例2 使用定理 3 中的对数性质来求解以下问题:
(a) log 4 2 + log 4 32 \log_4 2 + \log_4 32 log42+log432
(b) log 2 80 − log 2 5 \log_2 80 - \log_2 5 log280−log25
解
(a) 使用定理 3 中的性质 1,我们有:
log 4 2 + log 4 32 = log 4 ( 2 ⋅ 32 ) = log 4 64 = 3 \log_4 2 + \log_4 32 = \log_4 (2 \cdot 32) = \log_4 64 = 3 log42+log432=log4(2⋅32)=log464=3
因为 4 3 = 64 4^3 = 64 43=64。
(b) 使用定理 3 中的性质 2,我们有:
log 2 80 − log 2 5 = log 2 ( 80 5 ) = log 2 16 = 4 \log_2 80 - \log_2 5 = \log_2 \left( \frac{80}{5} \right) = \log_2 16 = 4 log280−log25=log2(580)=log216=4
因为 2 4 = 16 2^4 = 16 24=16。
指数函数在第 6.2 节中给出的极限,反映在以下对数函数的极限中。(与图 1 比较。)
4
如果 b > 1 b > 1 b>1,那么:
lim x → ∞ log b x = ∞ 和 lim x → 0 + log b x = − ∞ \lim_{x \to \infty} \log_b x = \infty \quad \text{和} \quad \lim_{x \to 0^+} \log_b x = -\infty x→∞limlogbx=∞和x→0+limlogbx=−∞
特别地,y 轴是曲线 y = log b x y = \log_b x y=logbx 的垂直渐近线。
例3 求 lim x → 0 log 10 ( tan 2 x ) \lim_{x \to 0} \log_{10} (\tan^2 x) limx→0log10(tan2x)。
解 当 x → 0 x \to 0 x→0 时,我们知道 t = tan 2 x → tan 2 0 = 0 t = \tan^2 x \to \tan^2 0 = 0 t=tan2x→tan20=0,并且 t t t 的值是正的。因此,根据定理 4(其中 b = 10 > 1 b = 10 > 1 b=10>1),我们有:
lim x → 0 log 10 ( tan 2 x ) = lim t → 0 + log 10 t = − ∞ \lim_{x \to 0} \log_{10} (\tan^2 x) = \lim_{t \to 0^+} \log_{10} t = -\infty x→0limlog10(tan2x)=t→0+limlog10t=−∞
自然对数
在所有可能的对数底数 b b b 中,我们将在下一节中看到,最方便的底数选择是数字 e e e,它在第 6.2 节中定义。以 e e e 为底的对数称为自然对数,并有一个特殊的符号表示:
log e x = ln x \log_e x = \ln x logex=lnx
如果我们将 b = e b = e b=e,并用“ ln \ln ln”代替 log e \log_e loge 在公式 (1) 和 (2) 中的符号,则自然对数函数的定义性质变为:
ln x = y ⟺ e y = x (5) \ln x = y \iff e^y = x \tag{5} lnx=y⟺ey=x(5)
ln ( e x ) = x x ∈ R e ln x = x x > 0 \begin{align*} \ln (e^x) &= x \quad x \in \mathbb{R}\\ e^{\ln x} &= x \quad x > 0 \end{align*} ln(ex)elnx=xx∈R=xx>0
特别地,如果我们取 x = 1 x = 1 x=1,我们得到:
ln e = 1 \ln e = 1 lne=1
例4 如果 ln x = 5 \ln x = 5 lnx=5,求 x x x。
解法 1 从性质 (5) 我们知道:
ln x = 5 means e 5 = x \ln x = 5 \quad \text{means} \quad e^5 = x lnx=5meanse5=x
因此, x = e 5 x = e^5 x=e5。
(如果使用 “( \ln )” 符号有困难,只需将其替换为 ( \log_e )。那么这个方程变为 ( \log_e x = 5 ),因此根据对数的定义,( e^5 = x )。)
解法 2
从方程 ln x = 5 \ln x = 5 lnx=5 开始。
对方程的两边应用指数函数:
e ln x = e 5 e^{\ln x} = e^5 elnx=e5
但根据消去方程 (6) 的第二条性质, e ln x = x e^{\ln x} = x elnx=x。因此, x = e 5 x = e^5 x=e5。
例5 解方程 e 5 − 3 x = 10 e^{5 - 3x} = 10 e5−3x=10。
解
我们对方程两边取自然对数并使用性质 (6):
ln ( e 5 − 3 x ) = ln 10 5 − 3 x = ln 10 3 x = 5 − ln 10 x = 1 3 ( 5 − ln 10 ) \begin{align*} \ln(e^{5 - 3x}) &= \ln 10\\ 5 - 3x &= \ln 10\\ 3x &= 5 - \ln 10\\ x &= \frac{1}{3}(5 - \ln 10) \end{align*} ln(e5−3x)5−3x3xx=ln10=ln10=5−ln10=31(5−ln10)
因为自然对数可以在科学计算器上找到,我们可以近似解:四舍五入到四位小数, x ≈ 0.8991 x \approx 0.8991 x≈0.8991。
例6 将 ln a + 1 2 ln b \ln a + \frac{1}{2} \ln b lna+21lnb 表示为单个对数。
解 使用对数的性质 3 和性质 1,我们得到:
ln a + 1 2 ln b = ln a + ln b 1 / 2 = ln a + ln b = ln ( a b ) \begin{align*} \ln a + \frac{1}{2} \ln b &= \ln a + \ln b^{1/2}\\ &= \ln a + \ln \sqrt{b}\\ &= \ln(a \sqrt{b}) \end{align*} lna+21lnb=lna+lnb1/2=lna+lnb=ln(ab)
7 换底公式 对于任意正数 b b b ( b ≠ 1 b \neq 1 b=1),我们有:
log b x = ln x ln b \log_b x = \frac{\ln x}{\ln b} logbx=lnblnx
证明 设 y = log b x y = \log_b x y=logbx。根据公式 (1),我们有 b y = x b^y = x by=x。对方程两边取自然对数,我们得到:
y ln b = ln x y \ln b = \ln x ylnb=lnx
因此:
y = ln x ln b y = \frac{\ln x}{\ln b} y=lnblnx
这证明了换底公式。
科学计算器通常都有计算自然对数的功能,因此公式 7 使我们可以使用计算器来计算任意底数的对数(如以下示例所示)。类似地,公式 7 还允许我们在图形计算器或计算机上绘制任意底数的对数函数。
例7 求 log 8 5 \log_8 5 log85 并精确到小数点后六位。
解 根据公式 7:
log 8 5 = ln 5 ln 8 ≈ 0.773976 \log_8 5 = \frac{\ln 5}{\ln 8} \approx 0.773976 log85=ln8ln5≈0.773976
自然对数的图像与增长
指数函数 y = e x y = e^x y=ex 及其反函数——自然对数函数的图像,如图 3 所示。由于曲线 y = e x y = e^x y=ex 以斜率 1 通过 y y y 轴,因此其反射曲线 y = ln x y = \ln x y=lnx 以斜率 1 通过 x x x 轴。

与所有底数大于 1 的其他对数函数一样,自然对数是一个定义在 ( 0 , ∞ ) (0, \infty) (0,∞) 上的连续递增函数,并且 y y y 轴是其垂直渐近线。
如果我们在公式 (4) 中将 b = e b = e b=e,那么我们有以下极限:
lim x → ∞ ln x = ∞ 和 lim x → 0 + ln x = − ∞ (8) \lim_{x \to \infty} \ln x = \infty \quad \text{和} \quad \lim_{x \to 0^+} \ln x = -\infty \tag{8} x→∞limlnx=∞和x→0+limlnx=−∞(8)
例8 绘制函数 y = ln ( x − 2 ) − 1 y = \ln(x - 2) - 1 y=ln(x−2)−1 的图像。
解 我们从图 3 中给出的
y
=
ln
x
y = \ln x
y=lnx 的图像开始。根据第 1.3 节的变换规则,我们将图像向右移动 2 个单位,得到
y
=
ln
(
x
−
2
)
y = \ln(x - 2)
y=ln(x−2) 的图像。然后我们将其向下移动 1 个单位,得到
y
=
ln
(
x
−
2
)
−
1
y = \ln(x - 2) - 1
y=ln(x−2)−1 的图像。(参见图 4。)

请注意,直线 x = 2 x = 2 x=2 是垂直渐近线,因为:
lim x → 2 + [ ln ( x − 2 ) − 1 ] = − ∞ \lim_{x \to 2^+} [\ln(x - 2) - 1] = -\infty x→2+lim[ln(x−2)−1]=−∞
我们已经看到,当 x → ∞ x \to \infty x→∞ 时, ln x → ∞ \ln x \to \infty lnx→∞。但这发生得非常缓慢。实际上, ln x \ln x lnx 的增长比 x x x 的任何正幂都要慢。为了说明这一点,我们比较了函数 y = ln x y = \ln x y=lnx 和 y = x 1 / 2 = x y = x^{1/2} = \sqrt{x} y=x1/2=x 的近似值,如表格中所示,并在图 5 和图 6 中绘制了它们的图像。
你可以看到,最初 y = x y = \sqrt{x} y=x 和 y = ln x y = \ln x y=lnx 的图像增长速率相当,但最终根函数远远超过了对数函数。事实上,我们将在第 6.8 节中展示:
lim x → ∞ ln x x p = 0 \lim_{x \to \infty} \frac{\ln x}{x^p} = 0 x→∞limxplnx=0
对于任何正幂 p p p。因此,对于较大的 x x x, ln x \ln x lnx 的值与 x p x^p xp 相比非常小。