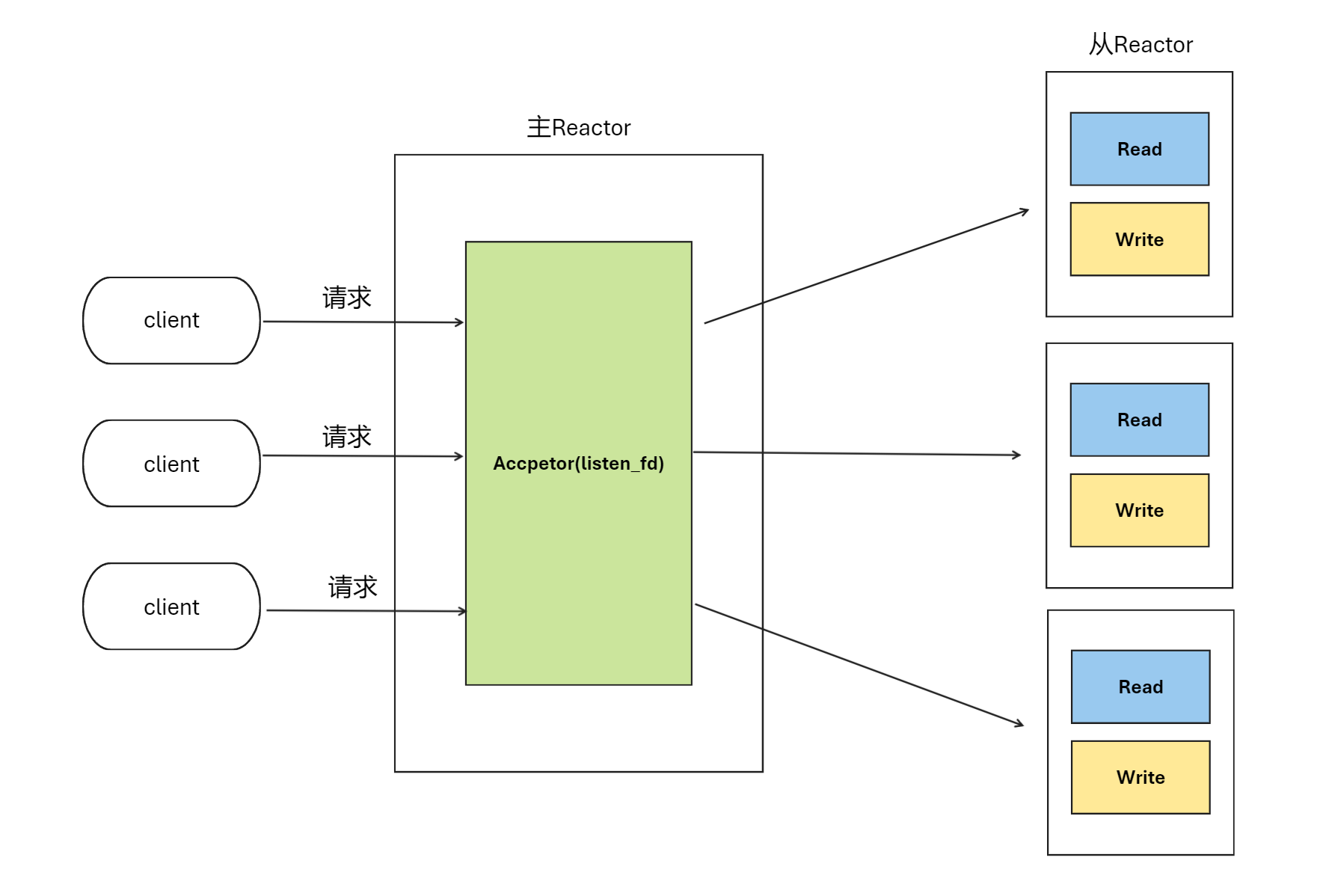
给你一个大小为 m x n 的整数矩阵 mat 和一个整数 target 。

从矩阵的 每一行 中选择一个整数，你的目标是 最小化 所有选中元素之 和 与目标值 target 的 绝对差 。

返回 最小的绝对差 。

a 和 b 两数字的 绝对差 是 a - b 的绝对值。

示例 1：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
输出：0
解释：一种可能的最优选择方案是：

• 第一行选出 1
• 第二行选出 5
• 第三行选出 7
  所选元素的和是 13 ，等于目标值，所以绝对差是 0 。

示例 2：

输入：mat = [[1],[2],[3]], target = 100
输出：94
解释：唯一一种选择方案是：

• 第一行选出 1
• 第二行选出 2
• 第三行选出 3
  所选元素的和是 6 ，绝对差是 94 。
  示例 3：
  
  输入：mat = [[1,2,9,8,7]], target = 6
  输出：1
  解释：最优的选择方案是选出第一行的 7 。
  绝对差是 1 。

提示：
m == mat.length
n == mat[i].length
1 <= m, n <= 70
1 <= mat[i][j] <= 70
1 <= target <= 800

动态规划

class Solution {
public:
    int minimizeTheDifference(vector<vector<int>>& mat, int target) {
        int m = mat.size(), n = mat[0].size();
        vector<int> f(target, 0);
        // 什么都不选时和为 0
        f[0] = true;
        // 最小的大于等于 target 的和
        int large = INT_MAX;
        for (int i = 0; i < m; ++i) {
            vector<int> g(target);
            int next_large = INT_MAX;
            for (int x: mat[i]) {
                for (int j = 0; j < target; ++j) {
                    if (f[j]) {
                        if (j + x >= target) {
                            next_large = min(next_large, j + x);
                        }
                        else {
                            g[j + x] = true;
                        }
                    }
                }
                if (large != INT_MAX) {
                    next_large = min(next_large, large + x);
                }
            }
            f = move(g);
            large = next_large;
        }

        int ans = large - target;
        for (int i = target - 1; i >= 0; --i) {
            if (f[i]) {
                ans = min(ans, target - i);
                break;
            }
        }
        return ans;
    }
};

首先定义一个向量f，f 是一个布尔数组，表示对于当前行，能否通过选择某些数字使得和等于该数组的下标。初始时，f[0] 设为 true，表示和为 0 是可以达到的。

对于每一行 i，使用一个新的数组 g 记录新的一轮可达和的情况。g[j] 表示是否可以通过选择这一行中的某些元素，使得和等于 j，也就是说g的作用是在计算完当前行的时候，赋给f，供下一行的循环使用，而f代表的是当前循环的上一行的组合可能性。

也就是说，在遍历每一个元素的时候，遍历j的目的就是判断是否有为true的f[j]，也就是之前行是否有和为j的组合，如果有的话，就说明x可以和j组成新的j+x的组合。这时候有两种情况，当j+x大于target的时候，我们就更新next_large，next_large的作用是记录当前行的大于target的最小值。

然后在循环某一行的不同元素时，都要更新next_large = min(next_large, large + x);。这是这道题目的不好理解的地方。这段代码在什么时候会起作用呢？我在一开始也陷入混乱，因为按道理来说，large是大于target的，但是j又是小于target的，next_large的更新是依赖于j+x的，也就是说对于同一个元素来说，large+x不可能比j+x小。

实际上没错，large+x不可能比j+x小，但是有一种情况，就是当遍历的某一个元素较小的时候，而且没有j+x大于target的情况，并且同一行其他元素的x较大的时候，这时候这个较小的x的large+x就可能是最接近target的值。

最后large记录的就是最接近target的值，我们令ans为large-target，然后遍历f，利用target-i是否有更小的差，然后更新ans，最后返回。