在数据结构与算法的面试中,顺序表是一个常见的考点。它作为一种基础的数据结构,涵盖了多种操作和概念,以下将详细介绍面试中关于顺序表常考的十大题目。
💝💝💝如果你对顺序表的概念与理解还存在疑惑,欢迎观看我之前的作品👉 【顺序表】
目录
一、顺序表的定义和基本概念
题目示例
⭐答案
二、顺序表的插入操作
题目示例
⭐答案
三、顺序表的删除操作
题目示例
⭐答案
四、顺序表的查找操作
题目示例
⭐答案
五、顺序表的遍历操作
题目示例
⭐答案
六、顺序表的初始化操作
题目示例
⭐答案
七、顺序表的扩容操作
题目示例
⭐答案
八、顺序表与其他数据结构的比较
题目示例
⭐答案
九、顺序表的排序操作(简单排序 - 冒泡排序)
题目示例
⭐答案
十、顺序表在实际应用中的场景
题目示例
⭐答案
一、顺序表的定义和基本概念
题目示例
- 来源:这是对顺序表基础知识的直接考查,通常出现在面试开场,用于初步了解应聘者对顺序表的理解程度。
- “请简要描述顺序表是什么,它的存储结构特点是什么?”
⭐答案
顺序表是用一组地址连续的存储单元依次存储线性表中的数据元素。它的特点是逻辑上相邻的数据元素在物理存储位置上也相邻。例如,若有一个顺序表存储整数,假设第一个元素存储在地址为 1000 的内存单元,每个元素占用 4 个字节的存储空间,那么第二个元素就存储在 1004 这个地址,以此类推。这种存储方式使得顺序表可以随机访问,即通过元素的序号(索引)能够在 O (1) 时间内访问到指定元素。
二、顺序表的插入操作
题目示例
- 来源:插入操作是顺序表的基本操作之一,考查应聘者对顺序表插入算法的理解和编写能力,以及对时间复杂度的分析能力,在各类数据结构相关面试中较为常见。
- “给定一个有 n 个元素的顺序表,编写一个函数实现将一个新元素插入到指定位置 i(0 <= i <= n)的功能,并分析其时间复杂度。”
⭐答案
- 算法步骤:
- 首先判断插入位置 i 是否合法,即 0 <= i <= n。如果不合法,返回错误信息。
- 若插入位置合法,从最后一个元素开始,将第 n - 1 个元素移动到第 n 个元素的位置,第 n - 2 个元素移动到第 n - 1 个元素的位置,依次类推,直到将第 i 个元素及其后面的元素都向后移动一位。
- 将新元素插入到位置 i 。
- 时间复杂度:在最坏的情况下(插入到表头),需要移动 n 个元素,所以时间复杂度为 O(n) 例如,顺序表中有元素 1, 2, 3,要在表头插入一个元素 0,需要将 1、2、3 依次向后移动一位,总共移动 3 次。
C++ 代码示例:
#include <iostream>
using namespace std;
class SeqList {
private:
int* data;
int capacity;
int size;
public:
SeqList(int initialCapacity) {
capacity = initialCapacity;
data = new int[capacity];
size = 0;
}
~SeqList() {
delete[] data;
}
// 在指定位置插入元素
void insert(int position, int value) {
if (position < 0 || position > size) {
cout << "Invalid position for insertion." << endl;
return;
}
if (size == capacity) {
int newCapacity = capacity * 2;
int* newData = new int[newCapacity];
for (int i = 0; i < size; i++) {
newData[i] = data[i];
}
delete[] data;
data = newData;
capacity = newCapacity;
}
for (int i = size; i > position; i--) {
data[i] = data[i - 1];
}
data[position] = value;
size++;
}
void printList() {
for (int i = 0; i < size; i++) {
cout << data[i] << " ";
}
cout << endl;
}
};
三、顺序表的删除操作
题目示例
- 来源:与插入操作相对应,删除操作也是顺序表的重要考点之一,面试官通过此类题目考查应聘者对顺序表删除算法的掌握情况和时间复杂度分析能力,在数据结构面试中较为常见。
- “写一个函数删除顺序表中指定位置 i(0 <= i < n)的元素,并说明时间复杂度。”
⭐答案
- 算法步骤:
- 先判断删除位置 i 是否合法,若不合法(i <0 或者 i>= n),返回错误信息。
- 从位置 i + 1 开始,将第 i + 1 个元素移动到第 i 个元素的位置,第 i + 2 个元素移动到第 i + 1 个元素的位置,依次类推,直到将最后一个元素移动到倒数第二个元素的位置。
- 表长减 1。
- 时间复杂度:在最坏的情况下(删除表头元素),需要移动 n - 1 个元素,所以时间复杂度为 O (n)。
- C++ 代码示例(可在上述 SeqList 类中添加以下方法)
// 删除指定位置的元素
void remove(int position) {
if (position < 0 || position >= size) {
cout << "Invalid position for removal." << endl;
return;
}
for (int i = position; i < size - 1; i++) {
data[i] = data[i + 1];
}
size--;
}
四、顺序表的查找操作
题目示例
- 来源:查找操作是数据结构中常用的基本操作之一,在数据结构和算法面试中经常出现,用于考查应聘者对顺序表查找算法的理解和实现能力,以及对时间复杂度的分析。
- “在顺序表中查找一个给定元素 x,返回其首次出现的位置,若不存在则返回 -1。分析时间复杂度。”
⭐答案
- 算法步骤:
- 从顺序表的第一个元素开始,依次比较每个元素与给定元素 x。
- 如果找到相等的元素,返回其位置(索引)。
- 如果遍历完整个顺序表都没有找到,则返回 -1。
- 时间复杂度:在最坏的情况下,需要遍历整个顺序表,时间复杂度为 O (n)。
- C++ 代码示例(可在上述 SeqList 类中添加以下方法):
// 查找指定元素的位置
int search(int value) {
for (int i = 0; i < size; i++) {
if (data[i] == value) {
return i;
}
}
return -1;
}五、顺序表的遍历操作
题目示例
- 来源:遍历操作是对顺序表整体操作的基础,常出现在数据结构基础面试环节或与其他操作结合考查,以检验应聘者对顺序表基本访问方式的掌握程度。
- “写一个函数实现顺序表的遍历,打印出顺序表中的所有元素。”
⭐答案
- C++ 代码示例(上述 SeqList 类中的 printList 方法即为遍历操作的实现):
void printList() {
for (int i = 0; i < size; i++) {
cout << data[i] << " ";
}
cout << endl;
}
六、顺序表的初始化操作
题目示例
- 来源:初始化是顺序表使用的前提,在涉及顺序表实际应用的面试问题中可能出现,考查应聘者对顺序表创建和初始状态设置的理解。
- “如何初始化一个顺序表,使其具有一定的初始容量?”
⭐答案
- C++ 代码示例(上述 SeqList 类的构造函数即为初始化操作的实现):
SeqList(int initialCapacity) {
capacity = initialCapacity;
data = new int[capacity];
size = 0;
}
七、顺序表的扩容操作
题目示例
- 来源:在实际应用中,顺序表可能会面临存储空间不足的情况,扩容操作是解决这一问题的关键,面试官通过此类题目考查应聘者对顺序表动态管理的理解和实现能力,常见于数据结构实际应用相关的面试中。
- “当顺序表已满,需要插入新元素时,如何实现顺序表的扩容?并分析扩容操作的时间复杂度。”
⭐答案
- 算法步骤(已在插入操作的代码中体现,这里再次说明):
- 首先创建一个新的、更大容量的存储数组。通常新容量是原容量的一定倍数(例如 2 倍)。
- 将原顺序表中的元素逐个复制到新的存储数组中。
- 释放原顺序表的存储空间,将新的存储数组赋值给原顺序表的指针。
- 时间复杂度:假设原顺序表有 n 个元素,扩容并复制元素的操作时间复杂度为 O (n),因为需要遍历原顺序表中的每个元素并复制到新数组中。
八、顺序表与其他数据结构的比较
题目示例
- 来源:了解不同数据结构的特点和适用场景是程序员的基本素养之一,通过此类题目考查应聘者对数据结构的综合理解和分析能力,在数据结构选型和优化相关的面试问题中经常出现。
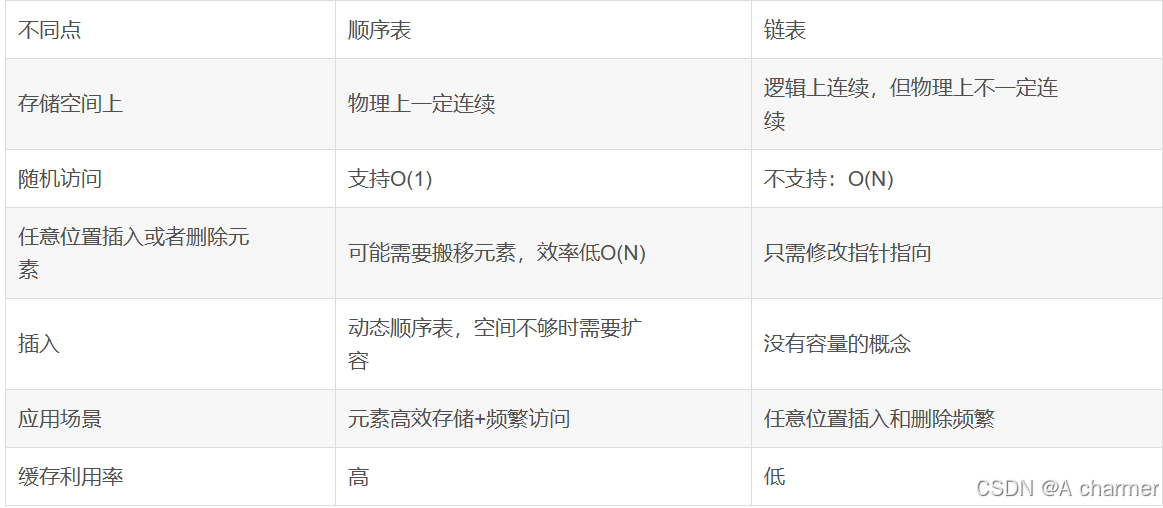
- “请比较顺序表和链表的优缺点。”
⭐答案
- 顺序表的优点:
- 可以随机访问,通过索引能在 O (1) 时间内访问任意元素。例如,在一个存储学生成绩的顺序表中,要查询第 5 个学生的成绩,能够快速定位。
- 存储密度高,因为不需要额外的指针来存储元素之间的关系,空间利用率相对较高。
- 顺序表的缺点:
- 插入和删除操作可能需要移动大量元素,时间复杂度为 O (n),效率较低。例如,在一个已经排好序的顺序表中插入一个新元素,可能会引起后续元素的大量移动。
- 大小固定(如果不进行扩容操作),初始化后容量不易改变。
- 链表的优点:
- 插入和删除操作灵活,只要修改指针即可,时间复杂度为 O (1)(在已知插入或删除位置的情况下)。例如,在一个链表中插入一个新节点,只需要修改相邻节点的指针。
- 链表的缺点:
- 不能随机访问,需要从头节点开始逐个遍历节点才能访问到指定元素,时间复杂度为 O (n)。
- 存储密度相对较低,因为每个节点除了存储数据元素外,还需要存储指向下一个节点的指针。
九、顺序表的排序操作(简单排序 - 冒泡排序)
题目示例
- 来源:排序是数据处理中的常见任务,考查应聘者对顺序表中数据排序算法的理解和应用能力,在算法和数据结构综合考查的面试中较为常见,冒泡排序是一种基础的排序算法,常被用于考查对排序原理的掌握。
- “用冒泡排序对顺序表进行排序,简述其原理和时间复杂度。”
⭐答案
- 原理:
- 从顺序表的第一个元素开始,比较相邻的两个元素。如果前面的元素大于后面的元素,则交换它们的位置。
- 对整个顺序表进行一次这样的操作后,最大的元素就会 “浮” 到最后。
- 然后对除了最后一个元素之外的其他元素重复上述过程,直到整个顺序表都有序。
- 时间复杂度:在最坏的情况下,需要进行 n (n - 1)/2 次比较和交换操作,所以时间复杂度为 O(n²)。
- C++ 代码示例(可在上述 SeqList 类中添加以下方法):
// 冒泡排序
void bubbleSort()
{
for (int i = 0; i < size - 1; i++)
{
for (int j = 0; j < size - i - 1; j++)
{
if (data[j] > data[j + 1])
{
int temp = data[j];
data[j] = data[j + 1];
data[j + 1] = temp;
}
}
}
}
十、顺序表在实际应用中的场景
题目示例
- 来源:考查应聘者对顺序表实际应用的理解和经验,以及能否将数据结构知识与实际软件开发场景相结合,在注重实践能力的面试中经常出现。
- “请举例说明顺序表在实际软件开发中的应用场景。”
⭐答案
- 数据存储和查询:如存储学生信息(学号、姓名、成绩等),如果经常需要根据学号(假设学号是连续分配的)来查询学生信息,顺序表是一个很好的选择,因为可以通过学号(索引)快速定位学生记录。
- 栈和队列的实现:栈可以用顺序表来实现,只需要在顺序表的一端(栈顶)进行插入和删除操作。对于队列,也可以用顺序表来实现,通过维护队头和队尾指针来进行入队和出队操作。
- 简单的缓存系统:可以用顺序表存储最近访问的数据,当缓存满时,可以按照一定的策略(如先进先出)删除元素,为新元素腾出空间。
通过对面试中顺序表常考十大题目的深入分析,我们不仅详细阐述了每个知识点的核心内容,还提供了丰富的 C++ 代码示例,帮助你更好地理解和掌握顺序表的相关操作。
💝💝💝感谢你看到最后,点个赞再走吧!💝💝💝
希望通过以下投票了解您对顺序表相关知识点的掌握情况和兴趣点,以便我们为您提供更有针对性的内容和更好的学习体验。



















