参考文献 代码随想录
一、修剪二叉搜索树
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:

输入:root = [1,0,2], low = 1, high = 2 输出:[1,null,2]
示例 2:

输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出:[3,2,null,1]
提示:
- 树中节点数在范围
[1, 104]内 0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
问题分析
如果当前的节点小于最小的值,那么根据二次搜索树的性质,左小右大,那么右边很有肯能在范围内,所以要去处理右边的树(不是只处理一个节点)在返回的时候,已经把不在范围内的给去掉了,反之大于最大的值,那么左边很有可能在返回内,所以要向左边遍历。
递归
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def trimBST(self, root, low, high):
"""
:type root: TreeNode
:type low: int
:type high: int
:rtype: TreeNode
"""
if root is None: # 如果为空直接返回None
return None
if root.val < low: # 当前节点的值小于最小的值,但是根据二次搜索树的性质,左小右大,那么右边很有肯能在范围内,所以要去处理右边的树(不是只处理一个节点)
return self.trimBST(root.right, low, high)
if root.val > high:
return self.trimBST(root.left, low, high)
root.left = self.trimBST(root.left, low, high)
root.right = self.trimBST(root.right, low, high)
return root迭代
因为二叉搜索树的有序性,不需要使用栈模拟递归的过程。
在剪枝的时候,可以分为三步:
- 将root移动到[L, R] 范围内,注意是左闭右闭区间
- 剪枝左子树
- 剪枝右子树
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def trimBST(self, root, low, high):
"""
:type root: TreeNode
:type low: int
:type high: int
:rtype: TreeNode
"""
if root is None: # 如果为空直接返回None
return None
# 处理头结点,让root移动到范围内,如果头节点的值
while root and (root.val < low or root.val > high): # 要使用while 不一定下一个就满足,有可能存在多个,首先要满足不为空,其次 如果满足不在范围内
if root.val < low: # 如果根节点小于最小的值,那么它的右节点可能存在满足的节点
root = root.right # 小于最小值,往右走
else:
root = root.left # 大于最大值,往左走
cur = root # 指针 指向根节点
# 此时root已经在范围内,需要处理左孩子
while cur: # 首先不为空一直处理
while cur.left and cur.left.val < low: # 其次左孩子 不为空
cur.left = cur.left.right
cur = cur.left
cur = root
# 此时root已经在范围内,处理右孩子大于R的情况
while cur:
while cur.right and cur.right.val > high:
cur.right = cur.right.left
cur = cur.right
return root二、将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵
平衡
二叉搜索树。
示例 1:
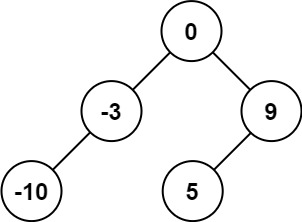
输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

示例 2:

输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
问题分析
每次分左右数组 ,然后 中间的节点连接,就是,第一次中间的节点是不是 数组长度整除于2然后得到一个值,因为为了保证它是平衡二叉树,然后它是有序的列表,然后左边的链接左边的右边链接右边的。
递归
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if not nums:
return
mid = len(nums) // 2
left = nums[: mid]
right = nums[mid + 1: ]
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBST(left)
root.right = self.sortedArrayToBST(right)
return root
迭代
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if not nums:
return
root = TreeNode(0) #初始化根节点
nodeQue = deque() # 放遍历的节点
leftQue = deque() # 保存左区间的小标
rightQue = deque() # 保存右区间的下标
nodeQue.append(root) # 根节点入队列
leftQue.append(0) # 0为左区间小标的初始位置
rightQue.append(len(nums) - 1) # len(nums) - 1 为右区间下下标的初始位置
while nodeQue:
curNode = nodeQue.popleft()
left = leftQue.popleft()
right = rightQue.popleft()
mid = (left + right) // 2
curNode.val = nums[mid] # 将mid对应的元素给中间节点
if left <= mid - 1: # 处理左
curNode.left = TreeNode(0)
nodeQue.append(curNode.left)
leftQue.append(left)
rightQue.append(mid - 1)
if right >= mid + 1: # 处理右
curNode.right = TreeNode(0)
nodeQue.append(curNode.right)
leftQue.append(mid + 1)
rightQue.append(right)
return root
三、把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: . - 力扣(LeetCode) 相同
示例 1:

输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1] 输出:[1,null,1]
示例 3:
输入:root = [1,0,2] 输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
问题分析
先从右开始累加,这样才能一定大于左的和其实这就是一棵树,大家可能看起来有点别扭,换一个角度来看,这就是一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13],是不是感觉这就简单了。
为什么变成数组就是感觉简单了呢?
因为数组大家都知道怎么遍历啊,从后向前,挨个累加就完事了,这换成了二叉搜索树,看起来就别扭了一些是不是。
那么知道如何遍历这个二叉树,也就迎刃而解了,从树中可以看出累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,然后顺序累加就可以了
递归
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def __init__(self):
self.prev = None
def convertBST(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if not root:
return
self.convertBST(root.right)
if self.prev:
root.val += self.prev.val
self.prev = root
self.convertBST(root.left)
return root
迭代
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def __init__(self):
self.prev = None
def convertBST(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if not root:
return
from collections import deque
stack = deque()
stack.append(root)
while stack: # 左中右,
cur = stack.pop()
if cur:
if cur.left:
stack.append(cur.left)
stack.append(cur)
stack.append(None)
if cur.right:
stack.append(cur.right)
else:
cur = stack.pop()
if self.prev:
cur.val += self.prev.val
self.prev = cur
return root
四、二叉树总结(遍历顺序)
二叉树的理论基础
- 关于二叉树,你该了解这些! (opens new window):二叉树的种类、存储方式、遍历方式、定义方式
#二叉树的遍历方式
- 深度优先遍历
- 二叉树:前中后序递归法 (opens new window):递归三部曲初次亮相
- 二叉树:前中后序迭代法(一) (opens new window):通过栈模拟递归
- 二叉树:前中后序迭代法(二)统一风格(opens new window)
- 广度优先遍历
- 二叉树的层序遍历 (opens new window):通过队列模拟
#求二叉树的属性
- 二叉树:是否对称(opens new window)
- 递归:后序,比较的是根节点的左子树与右子树是不是相互翻转
- 迭代:使用队列/栈将两个节点顺序放入容器中进行比较
- 二叉树:求最大深度(opens new window)
- 递归:后序,求根节点最大高度就是最大深度,通过递归函数的返回值做计算树的高度
- 迭代:层序遍历
- 二叉树:求最小深度(opens new window)
- 递归:后序,求根节点最小高度就是最小深度,注意最小深度的定义
- 迭代:层序遍历
- 二叉树:求有多少个节点(opens new window)
- 递归:后序,通过递归函数的返回值计算节点数量
- 迭代:层序遍历
- 二叉树:是否平衡(opens new window)
- 递归:后序,注意后序求高度和前序求深度,递归过程判断高度差
- 迭代:效率很低,不推荐
- 二叉树:找所有路径(opens new window)
- 递归:前序,方便让父节点指向子节点,涉及回溯处理根节点到叶子的所有路径
- 迭代:一个栈模拟递归,一个栈来存放对应的遍历路径
- 二叉树:递归中如何隐藏着回溯(opens new window)
- 详解二叉树:找所有路径 (opens new window)中递归如何隐藏着回溯
- 二叉树:求左叶子之和(opens new window)
- 递归:后序,必须三层约束条件,才能判断是否是左叶子。
- 迭代:直接模拟后序遍历
- 二叉树:求左下角的值(opens new window)
- 递归:顺序无所谓,优先左孩子搜索,同时找深度最大的叶子节点。
- 迭代:层序遍历找最后一行最左边
- 二叉树:求路径总和(opens new window)
- 递归:顺序无所谓,递归函数返回值为bool类型是为了搜索一条边,没有返回值是搜索整棵树。
- 迭代:栈里元素不仅要记录节点指针,还要记录从头结点到该节点的路径数值总和
#二叉树的修改与构造
- 翻转二叉树(opens new window)
- 递归:前序,交换左右孩子
- 迭代:直接模拟前序遍历
- 构造二叉树(opens new window)
- 递归:前序,重点在于找分割点,分左右区间构造
- 迭代:比较复杂,意义不大
- 构造最大的二叉树(opens new window)
- 递归:前序,分割点为数组最大值,分左右区间构造
- 迭代:比较复杂,意义不大
- 合并两个二叉树(opens new window)
- 递归:前序,同时操作两个树的节点,注意合并的规则
- 迭代:使用队列,类似层序遍历
#求二叉搜索树的属性
-
二叉搜索树中的搜索(opens new window)
- 递归:二叉搜索树的递归是有方向的
- 迭代:因为有方向,所以迭代法很简单
-
是不是二叉搜索树(opens new window)
- 递归:中序,相当于变成了判断一个序列是不是递增的
- 迭代:模拟中序,逻辑相同
-
求二叉搜索树的最小绝对差(opens new window)
- 递归:中序,双指针操作
- 迭代:模拟中序,逻辑相同
-
求二叉搜索树的众数(opens new window)
-
递归:中序,清空结果集的技巧,遍历一遍便可求众数集合
-
二叉搜索树转成累加树(opens new window)
-
递归:中序,双指针操作累加
-
迭代:模拟中序,逻辑相同
-
#二叉树公共祖先问题
- 二叉树的公共祖先问题(opens new window)
- 递归:后序,回溯,找到左子树出现目标值,右子树节点目标值的节点。
- 迭代:不适合模拟回溯
- 二叉搜索树的公共祖先问题(opens new window)
- 递归:顺序无所谓,如果节点的数值在目标区间就是最近公共祖先
- 迭代:按序遍历
#二叉搜索树的修改与构造
注意在普通二叉树的属性中,我用的是一般为后序,例如单纯求深度就用前序,二叉树:找所有路径 (opens new window)也用了前序,这是为了方便让父节点指向子节点。
- 二叉搜索树中的插入操作(opens new window)
- 递归:顺序无所谓,通过递归函数返回值添加节点
- 迭代:按序遍历,需要记录插入父节点,这样才能做插入操作
- 二叉搜索树中的删除操作(opens new window)
- 递归:前序,想清楚删除非叶子节点的情况
- 迭代:有序遍历,较复杂
- 修剪二叉搜索树(opens new window)
- 递归:前序,通过递归函数返回值删除节点
- 迭代:有序遍历,较复杂
- 构造二叉搜索树(opens new window)
- 递归:前序,数组中间节点分割
- 迭代:较复杂,通过三个队列来模拟
-
涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
-
求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
-
求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。