题目描述

有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。
你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
例如：[1, 3, −1, −3, 5, 3, 6, 7] k=3。

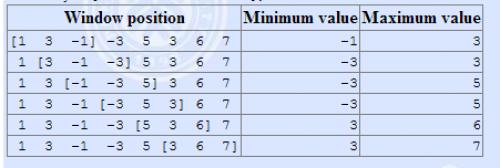
有一个长为 n 的序列 a，以及一个大小为 k 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

输入格式

输入一共有两行，第一行有两个正整数 n, k。
第二行 n 个整数，表示序列 a。

输出格式

输出包含两个。
第一行输出，从左至右，每个位置滑动窗口中的最小值。
第二行输出，从左至右，每个位置滑动窗口中的最大值。

数据范围

对于 50% 的数据，1≤n≤10^5；
对于 100% 的数据，1≤k≤n≤10^6, ai∈[−2^31,2^31)。

输入样例

8 3
1 3 -1 -3 5 3 6 7

输出样例

-1 -3 -3 -3 3 3
3 3 5 5 6 7

注释版代码

//http://47.110.135.197/problem.php?id=5761
#include<iostream>
using namespace std;
const int N=1000010;
int a[N];
int q[N];//q[]里面存下标
int hh,tt=-1;
int main()
{
	int n,k;
	scanf("%d %d",&n,&k);
	for(int i=0;i<n;i++)
	{
		scanf("%d",&a[i]);
	}
	//求区间最小值
	for(int i=0;i<n;i++)
	{
		//因为每次只移动一位，所以用if
		if(hh<=tt&&i-k+1>q[hh]) hh++;//i为当前下标，k为区间长度，i-k+1即为区间左边界，当他超出hh的下标，此时需要将hh++
		while(hh<=tt&&a[i]<a[q[tt]]) tt--;
		//如果当前的元素a[i]小于队尾元素，那么说明只要a[i]在，队尾元素就永无出头之日
		//而且a[i]比队尾元素晚进队列，那么就晚出队列，所以只要a[i]在队列，队尾元素就没用了，弹出去就行了，tt--
		q[++tt]=i;//把当前i的下标存入队列
		//如果队列里的数还不到区间的长度那不输出
		if(i>=k-1) printf("%d ",a[q[hh]]);
	}
	printf("\n");
	hh=0,tt=-1;//初始化
	//求区间最大值（反之）
	for(int i=0;i<n;i++)
	{
		if(hh<=tt&&i-k+1>q[hh]) hh++;
		while(hh<=tt&&a[i]>a[q[tt]]) tt--;
		q[++tt]=i;
		if(i>=k-1) printf("%d ",a[q[hh]]);
	}
	return 0;
}