目录
1、城市间货物运输I
2、城市间货物运输II
3、城市间货物运输III
1、城市间货物运输I
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。
城市 1 到城市 n 之间可能会出现没有路径的情况,同时保证道路网络中不存在任何负权回路。
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v (单向图)。
输出描述
如果能够从城市 1 到连通到城市 n, 请输出一个整数,表示运输成本。如果该整数是负数,则表示实现了盈利。如果从城市 1 没有路径可达城市 n,请输出 "unconnected"。
输入示例
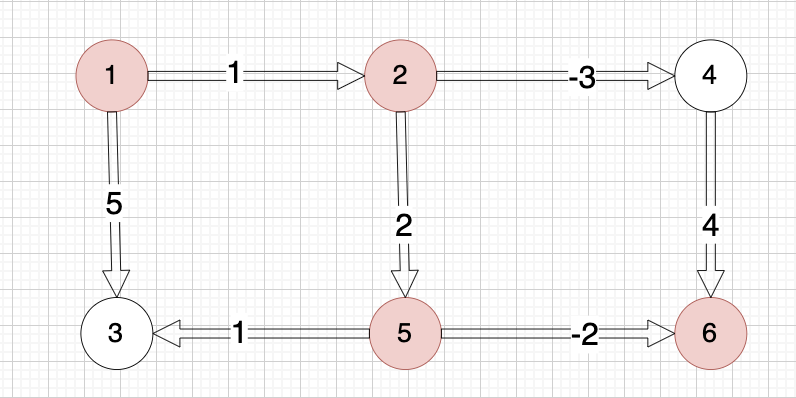
6 7 5 6 -2 1 2 1 5 3 1 2 5 2 2 4 -3 4 6 4 1 3 5
输出示例
1
提示信息
示例中最佳路径是从 1 -> 2 -> 5 -> 6,路上的权值分别为 1 2 -2,最终的最低运输成本为 1 + 2 + (-2) = 1。
示例 2:
4 2
1 2 -1
3 4 -1在此示例中,无法找到一条路径从 1 通往 4,所以此时应该输出 "unconnected"。
数据范围:
1 <= n <= 1000;
1 <= m <= 10000;-100 <= v <= 100;
思路:上一次对Bellman_ford算法进行了讲解,主要解决负权单源最短路径问题。
但是起始可以对上面的算法进行优化,称为Bellman_ford 队列优化算法,又称为SPFA算法。
因为每次松弛操作只会更新一条路径,所以如果每次松弛操作都对每条边进行则会造成冗余计算,因为后续的结果会将前面的结果覆盖掉,比如进行第一次松弛操作,那么则会更新从源点出发的一条路径,如果按照之前没有优化的算法,那么则会将每条边进行操作,但是有效的就只有从源点出发的第一条路径,第二次松弛操作时,有效的是从源点出发跨两条路径的路径,这时就会对第一次的跨两条路径的值覆盖掉,以此类推,所以其实可以不用在每次松弛操作时都对每一条边更新。
这也就是为什么需要优化的地方。理解了这一点其实就比较简单了,直白点说就是添加了一个队列来存储当前访问的结点。当然,为了在每次松弛操作时避免重复添加已经更新过的边,可以使用一个visited数组来进行记录。
#include<iostream>
#include<vector>
#include<queue>
#include<climits>
#include<list>
using namespace std;
struct Edge{
int to_node;
int val;
Edge(int to, int v): to_node(to), val(v){}
};
int main(){
int n, m;
while(cin >> n >> m){
vector<list<Edge>> grid(n + 1);//使用邻接表来存储图
vector<bool> isInQueue(n + 1, false);//记录结点入队列的情况
int s, t, val;
for(int i = 0; i < m; i ++){
cin >> s >> t >> val;
grid[s].push_back(Edge(t, val));
}
vector<int> minDist(n + 1, INT_MAX);
queue<int> que;//将访问结点添加入队列
que.push(1);//将源点放入队列
minDist[1] = 0;//源点到自身的最短距离为0
while(!que.empty()){
int node = que.front(); que.pop();
isInQueue[node] = false;//出队列后就将状态标记为false
list<Edge> keys = grid[node];
for(Edge edge: keys){
int to = edge.to_node;
int val = edge.val;
if(minDist[node] != INT_MAX && minDist[node] + val < minDist[to]){
minDist[to] = minDist[node] + val;//更新minDist的值
if(isInQueue[to] == false){
que.push(to);//将结点加入队列
isInQueue[to] = true;//入队列后置状态为true
}
}
}
}
if(minDist[n] == INT_MAX) cout << "unconnected" << endl;
else cout << minDist[n] << endl;
}
}2、城市间货物运输II
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
然而,在评估从城市 1 到城市 n 的所有可能路径中综合政府补贴后的最低运输成本时,存在一种情况:图中可能出现负权回路。负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。为了避免货物运输商采用负权回路这种情况无限的赚取政府补贴,算法还需检测这种特殊情况。
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。同时能够检测并适当处理负权回路的存在。
城市 1 到城市 n 之间可能会出现没有路径的情况
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
输出描述
如果没有发现负权回路,则输出一个整数,表示从城市
1到城市n的最低运输成本(包括政府补贴)。如果该整数是负数,则表示实现了盈利。如果发现了负权回路的存在,则输出 "circle"。如果从城市 1 无法到达城市 n,则输出 "unconnected"。
输入示例
4 4 1 2 -1 2 3 1 3 1 -1 3 4 1
输出示例
circle
提示信息
路径中存在负权回路,从 1 -> 2 -> 3 -> 1,总权值为 -1,理论上货物运输商可以在该回路无限循环赚取政府补贴,所以输出 "circle" 表示已经检测出了该种情况。
数据范围:
1 <= n <= 1000;
1 <= m <= 10000;-100 <= v <= 100;
思路:之前讲的都是不涉及到负权回路的。而这道题涉及到了负权回路的问题,如果存在一个回路,路径总和为负值,那么就可能会通过无限绕圈,从而无限度的增大收益,这显然是不合理的。
我们之前说过,Bellman_ford算法只要松弛n-1次即可,因为松弛次数多了,其实minDist数组的值其实并不会变了,这是针对不存在负权回路的时候。这里插一句,其实如果存在正权回路的话,Bellman_ford算法也是可以用的,因为不会存在回路路径权值总和无限绕圈的情况,总会因为权值太大以及遍历结束而退出循环,所以最终是能得到结果的。
关键就在于如何记录到存在负权回路呢?
如果存在负权回路,那么再多进行一次绕圈的时候,minDist必然会更新!
所以我们可以进行n次松弛操作,比n-1多一次,因为如果不存在负权回路多进行一次也无妨,但是如果存在负权回路,那么就能够进行标记,从而输出结果。
#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main(){
int n, m;
while(cin >> n >> m){
vector<vector<int>> grid;
int s, t, val;
for(int i = 0; i < m; i ++){
cin >> s >> t >> val;
grid.push_back({s, t, val});
}
vector<int> minDist(n + 1, INT_MAX);
minDist[1] = 0;
bool flag = false;//标记是否存在负权回路
for(int i = 0; i <= n; i ++){//松弛次数为n次
for(vector<int>& edge: grid){
int from = edge[0];
int to = edge[1];
int val = edge[2];
if(i < n){
if(minDist[from] != INT_MAX && minDist[from] + val < minDist[to]){
minDist[to] = minDist[from] + val;
}
}else{//这里在进行第n次松弛时发现minDist还在发生变化,说明确实存在负权回路
if(minDist[from] != INT_MAX && minDist[from] + val < minDist[to]) flag = true;
}
}
}
if(flag) cout << "circle" << endl;
else if(minDist[n] == INT_MAX) cout << "unconnected" << endl;
else cout << minDist[n] << endl;
}
}当然可以使用SPFA来做,但是这里需要对结点入队列的次数进行监控。对于一个稠密图来说,最复杂的情况就是一个结点存在n-1条边指向该结点,所以一个结点最多只能有n-1次入队列,所以一旦入队列的次数大于了n-1,那就说明存在了负权回路(正权回路会因为权值大于之前的minDist而进不去条件判断)。
#include<iostream>
#include<vector>
#include<list>
#include<queue>
#include<climits>
using namespace std;
struct Edge{
int to;
int val;
Edge(int to, int val): to(to), val(val){}
};
int main(){
int n, m;
while(cin >> n >> m){
vector<list<Edge>> grid(n + 1);
int s, t, val;
for(int i = 0; i < m; i ++){
cin >> s >> t >> val;
grid[s].push_back(Edge(t, val));
}
vector<int> minDist(n + 1, INT_MAX);
vector<int> count(n + 1, 0);//记录每个结点入队列的次数
queue<int> que;
minDist[1] = 0;
count[1] ++;
que.push(1);
bool flag = false;//标记是否具有负权回路
while(!que.empty()){
int node = que.front();que.pop();
for(Edge edge: grid[node]){
int to = edge.to;
int val = edge.val;
if(minDist[node] + val < minDist[to]){
minDist[to] = minDist[node] + val;
que.push(to);
count[to] ++;
if(count[to] == n){//当没有负权回路的时候,每个结点最多可以被加入到队列中n-1次,当超过后就说明存在了负权回路
flag = true;
while(!que.empty()) que.pop();//这里开始准备跳出内层for循环和外层while循环了
break;
}
}
}
}
if(flag) cout << "circle" << endl;
else if(minDist[n] == INT_MAX) cout << "unconnected" << endl;
else cout << minDist[n] << endl;
}
}3、城市间货物运输III
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请计算在最多经过 k 个城市的条件下,从城市 src 到城市 dst 的最低运输成本。
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
最后一行包含三个正整数,src、dst、和 k,src 和 dst 为城市编号,从 src 到 dst 经过的城市数量限制。
输出描述
输出一个整数,表示从城市 src 到城市 dst 的最低运输成本,如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径,则输出 "unreachable",表示不存在符合条件的运输方案。
输入示例
6 7 1 2 1 2 4 -3 2 5 2 1 3 5 3 5 1 4 6 4 5 6 -2 2 6 1
输出示例
0
提示信息
从 2 -> 5 -> 6 中转一站,运输成本为 0。
1 <= n <= 1000;
1 <= m <= 10000;
-100 <= v <= 100;
思路:这里对路径条数进行了限制。因为最多能经过k个结点,所以能走的边数为k+1,比如1->2->3->4,存在这样一条路径,那么k=2的时候,从1到4就需要走3条路径。注意这里的k=2是最多能经过的结点,也可以少于它,只要最后是最短的即可。
之前我们知道,每次进行一次松弛操作就能更新一条边,那么这里最多能走k+1条边,那就进行k+1次松弛操作即可!
但是这里需要注意题目没有明确说明不存在负权回路,所以还需要考虑一下负权回路的问题,如果说按照上面的思路去做,碰到负权回路的时候就会出错,原因就在于在每一次松弛操作的时候会更新每一条边的值(注意这里没有对Bellman_ford优化),而在进行更新新的一条边时会使用本次松弛操作的该边前一条边的结果,这样操作后的最终结果已经不再是只最多经过k个结点,最多经过k+1条边所得到的结果了,而是经过更多结点,更多条边的结果,所以会导致错误。
所以我们需要使用一个tmp数组来在每次更新之前记录以下minDist数组的情况,使用的时候只会更新本次松弛操作所能够更新的边,从而保证最终结果的正确性。
#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main(){
int n, m;
while(cin >> n >> m){
vector<vector<int>> grid;
int s, t, val;
for(int i = 0; i < m; i ++){
cin >> s >> t >> val;
grid.push_back({s, t, val});
}
int src, des, k;
cin >> src >> des >> k;
vector<int> minDist(n + 1, INT_MAX);
vector<int> minDist_copy(n + 1);//记录minDist的值
minDist[src] = 0;
for(int i = 1; i <= k + 1; i ++){//最多经过k个城市,所以最多松弛k+1次
minDist_copy = minDist;//每次松弛前都记录minDist之前的值,以防被更新
for(vector<int>& edge: grid){
int from = edge[0];
int to = edge[1];
int val = edge[2];
if(minDist_copy[from] != INT_MAX && minDist_copy[from] + val < minDist[to]){
minDist[to] = minDist_copy[from] + val;
}
}
}
if(minDist[des] == INT_MAX) cout << "unreachable" << endl;
else cout << minDist[des] << endl;
}
}这里还是可以使用SPFA进行优化,但是基本逻辑还是跟上面的一样,需要注意的是一些小细节,比如可以使用visited数组避免结点重复进入队列,需要记录前面一次入队列的元素的个数等等,了解了这些其实就没什么问题了。
#include<iostream>
#include<vector>
#include<list>
#include<queue>
#include<climits>
using namespace std;
struct Edge{
int to;
int val;
Edge(int to, int val): to(to), val(val){}
};
int main(){
int n, m;
while(cin >> n >> m){
vector<list<Edge>> grid(n + 1);//注意邻接表存储时,链表这个地方需要指定大小为n+1
int s, t, val;
for(int i = 0; i < m; i ++){
cin >> s >> t >> val;
grid[s].push_back(Edge(t, val));
}
int src, des, k;
cin >> src >> des >> k;
k ++;
vector<int> minDist(n + 1, INT_MAX);
vector<int> minDist_copy(n + 1);//记录minDist的值
minDist[src] = 0;
queue<int> que;
que.push(src);
int que_size;//记录队列中元素的个数
while(k -- && !que.empty()){
minDist_copy = minDist;
vector<bool> visited(n + 1, false);//每次松弛都记录以下结点是否已经进入过队列了
que_size = que.size();//记录前一次进入队列中结点数量的大小
while(que_size --){
int node = que.front(); que.pop();
for(Edge edge : grid[node]){
int to = edge.to;
int val = edge.val;
if(minDist_copy[node] + val < minDist[to]){
minDist[to] = minDist_copy[node] + val;
if(visited[to] == false){
visited[to] = true;
que.push(to);
}
}
}
}
}
if(minDist[des] == INT_MAX) cout << "unreachable" << endl;
else cout << minDist[des] << endl;
}
}感谢你的阅读,希望我的文章能够给你帮助,如果有帮助,麻烦点赞加收藏,或者点点关注,非常感谢。
如果有什么问题欢迎评论区讨论!