PDD
昨天聊到 PDD 可能会执行双休政,当中提到了「PDD 的年包在互联网行业中名列前茅」,不少同学一下子来兴趣了。
我这里也从脉脉中找到一份较新的 PDD 各岗位薪资一览表:
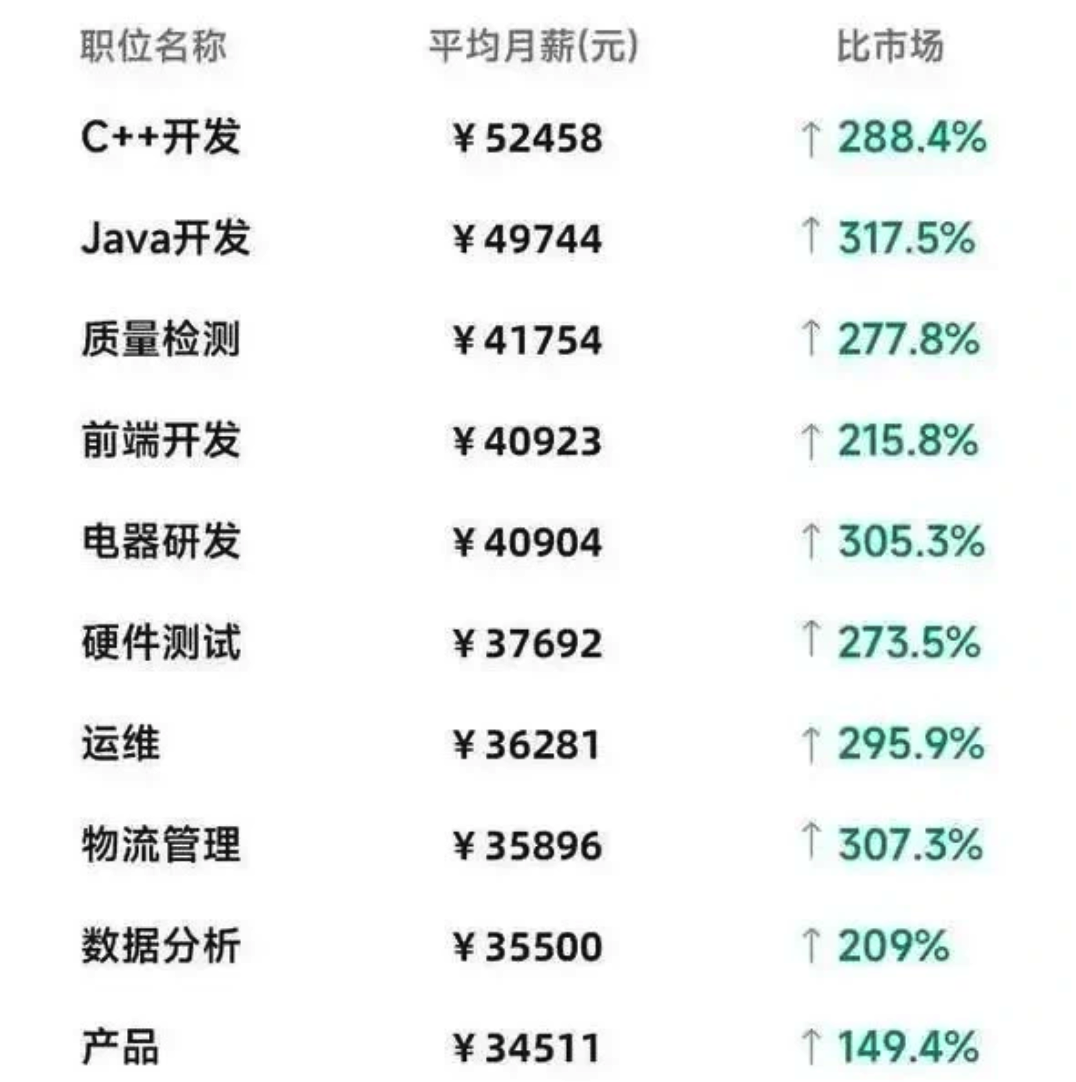
注意,这里的平均月薪的计算方式是年收入除以 12,别忘了昨天我们提到的,拼多多普遍都是 15~16 薪(1~2个月的年终奖 + 1.5~2个月的加班费),海外组普遍是 16~18 薪。
因此,如果不考虑股票期权,想算一下真实的 base 是多少,大概将上述数字乘个 0.77 就差不多了(将 15.5 薪的年包等比折算回 12 薪)。
这里帮大家速算一些感兴趣的岗位:
-
C++:平均 base 约 40k -
Java:平均 base 约 38k -
前端:平均 base 约 30k -
硬件:平均 base 约 28k -
运维:平均 base 约 27k -
数据分析:平均 base 约 27k -
产品:平均 base 约 26k
由此可见,即使不算加班费,PDD 的 base 也属于有竞争力的一档。
大家还想看哪个厂的薪资一览,欢迎评论区留言。
...
回归主线。
来一道和「秋招」相关的算法原题。
题目描述
平台:LeetCode
题号:1763
当一个字符串 s 包含的每一种字母的大写和小写形式同时出现在 s 中,就称这个字符串 s 是美好字符串。
比方说,"abABB" 是美好字符串,因为 'A' 和 'a' 同时出现了,且 'B' 和 'b' 也同时出现了。
然而,"abA" 不是美好字符串因为 'b' 出现了,而 'B' 没有出现。
给你一个字符串 s ,请你返回 s 最长的美好子字符串。
如果有多个答案,请你返回最早出现的一个。如果不存在美好子字符串,请你返回一个空字符串。
示例 1:
输入:s = "YazaAay"
输出:"aAa"
解释:"aAa" 是一个美好字符串,因为这个子串中仅含一种字母,其小写形式 'a' 和大写形式 'A' 也同时出现了。
"aAa" 是最长的美好子字符串。
示例 2:
输入:s = "Bb"
输出:"Bb"
解释:"Bb" 是美好字符串,因为 'B' 和 'b' 都出现了。整个字符串也是原字符串的子字符串。
示例 3:
输入:s = "c"
输出:""
解释:没有美好子字符串。
示例 4:
输入:s = "dDzeE"
输出:"dD"
解释:"dD" 和 "eE" 都是最长美好子字符串。
由于有多个美好子字符串,返回 "dD" ,因为它出现得最早。
提示:
-
-
s只包含大写和小写英文字母。
朴素解法
数据范围只有 ,最为简单的做法是枚举所有的子串( 复杂度为 ),然后对子串进行合法性检查( 复杂度为 ),整体复杂度为 ,可以过。
Java 代码:
class Solution {
public String longestNiceSubstring(String s) {
int n = s.length();
String ans = "";
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (j - i + 1 > ans.length() && check(s.substring(i, j + 1))) ans = s.substring(i, j + 1);
}
}
return ans;
}
boolean check(String s) {
Set<Character> set = new HashSet<>();
for (char c : s.toCharArray()) set.add(c);
for (char c : s.toCharArray()) {
char a = Character.toLowerCase(c), b = Character.toUpperCase(c);
if (!set.contains(a) || !set.contains(b)) return false;
}
return true;
}
}
C++ 代码:
class Solution {
public:
string longestNiceSubstring(string s) {
int n = s.length();
string ans = "";
for (int i = 0; i < n; i++) {
for (int j = i + 1; j <= n; j++) {
string sub = s.substr(i, j - i);
if (j - i > ans.length() && check(sub)) ans = sub;
}
}
return ans;
}
bool check(const string& s) {
unordered_set<char> set;
for (char c : s) set.insert(c);
for (char c : s) {
char a = tolower(c), b = toupper(c);
if (set.find(a) == set.end() || set.find(b) == set.end()) return false;
}
return true;
}
};
Python 代码:
class Solution:
def longestNiceSubstring(self, s: str) -> str:
n = len(s)
ans = ""
for i in range(n):
for j in range(i + 1, n):
if j - i + 1 > len(ans) and self.check(s[i:j+1]):
ans = s[i:j+1]
return ans
def check(self, s):
set_ = set()
for c in s:
set_.add(c)
for c in s:
a, b = c.lower(), c.upper()
if a not in set_ or b not in set_:
return False
return True
-
时间复杂度: -
空间复杂度:
前缀和优化
在 check 中,我们不可避免的遍历整个子串,复杂度为
。
该过程可以使用前缀和思想进行优化:「构建二维数组
来记录子串的词频,
为一个长度为
的数组,用于记录字符串 s 中下标范围为
的词频。即
所代表的含义为在子串
中字符
的出现次数。」
那么利用「容斥原理」,对于 s 的任意连续段
所代表的子串中的任意字符
的词频,我们可以作差算得:
这样我们在 check 实现中,只要检查
个字母对应的大小写词频(ASCII 相差
),是否同时为
或者同时不为
即可,复杂度为
。
Java 代码:
class Solution {
public String longestNiceSubstring(String s) {
int n = s.length();
int[][] cnt = new int[n + 1][128];
for (int i = 1; i <= n; i++) {
char c = s.charAt(i - 1);
cnt[i] = cnt[i - 1].clone();
cnt[i][c - 'A']++;
}
int idx = -1, len = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (j - i + 1 <= len) continue;
int[] a = cnt[i], b = cnt[j + 1];
if (check(a, b)) {
idx = i; len = j - i + 1;
}
}
}
return idx == -1 ? "" : s.substring(idx, idx + len);
}
boolean check(int[] a, int[] b) {
for (int i = 0; i < 26; i++) {
int low = b[i] - a[i], up = b[i + 32] - a[i + 32]; // 'A' = 65、'a' = 97
if (low != 0 && up == 0) return false;
if (low == 0 && up != 0) return false;
}
return true;
}
}
C++ 代码:
class Solution {
public:
string longestNiceSubstring(string s) {
int n = s.length();
vector<vector<int>> cnt(n + 1, vector<int>(128));
for (int i = 1; i <= n; i++) {
char c = s[i - 1];
cnt[i] = cnt[i - 1];
cnt[i][c - 'A'] += 1;
}
int idx = -1, len = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (j - i + 1 <= len) continue;
if (check(cnt[i], cnt[j + 1])) {
idx = i; len = j - i + 1;
}
}
}
return idx == -1 ? "" : s.substr(idx, len);
}
bool check(const vector<int>& a, const vector<int>& b) {
for (int i = 0; i < 26; i++) {
int low = b[i] - a[i], up = b[i + 32] - a[i + 32];
if ((low != 0 && up == 0) || (low == 0 && up != 0)) return false;
}
return true;
}
};
Python 代码:
class Solution:
def longestNiceSubstring(self, s: str) -> str:
n = len(s)
cnt = [[0] * 128 for _ in range(n + 1)]
for i in range(1, n + 1):
c = s[i - 1]
cnt[i] = cnt[i - 1].copy()
cnt[i][ord(c) - ord('A')] += 1
idx, lenv = -1, 0
for i in range(n):
for j in range(i + 1, n):
if j - i + 1 <= lenv:
continue
if self.check(cnt[i], cnt[j + 1]):
idx, lenv = i, j - i + 1
return "" if idx == -1 else s[idx: idx + lenv]
def check(self, a, b):
for i in range(26):
low = b[i] - a[i]
up = b[i + 32] - a[i + 32]
if (low != 0 and up == 0) or (low == 0 and up != 0):
return False
return True
-
时间复杂度:令 为字符集大小,本题固定为 ,构建 cnt的复杂度为 ;枚举所有子串复杂度为 ;check的复杂度为 。整体复杂度为 -
空间复杂度:
二进制优化
更进一步,对于某个子串而言,我们只关心大小写是否同时出现,而不关心出现次数。
因此我们无须使用二维数组来记录具体的词频,可以在枚举子串时,使用两个 int 的低
位分别记录大小写字母的出现情况,利用枚举子串时右端点后移,维护两变量,当且仅当两变量相等时,满足
个字母的大小写同时出现或同时不出现。
Java 代码:
class Solution {
public String longestNiceSubstring(String s) {
int n = s.length(), idx = -1, len = 0;
for (int i = 0; i < n; i++) {
int a = 0, b = 0;
for (int j = i; j < n; j++) {
char c = s.charAt(j);
if (c >= 'a' && c <= 'z') a |= (1 << (c - 'a'));
else b |= (1 << (c - 'A'));
if (a == b && j - i + 1 > len) {
idx = i; len = j - i + 1;
}
}
}
return idx == -1 ? "" : s.substring(idx, idx + len);
}
}
C++ 代码:
class Solution {
public:
string longestNiceSubstring(string s) {
int n = s.length(), idx = -1, len = 0;
for (int i = 0; i < n; i++) {
int a = 0, b = 0;
for (int j = i; j < n; j++) {
char c = s[j];
if (islower(c)) a |= (1 << (c - 'a'));
else b |= (1 << (c - 'A'));
if (a == b && j - i + 1 > len) {
idx = i; len = j - i + 1;
}
}
}
return idx == -1 ? "" : s.substr(idx, len);
}
};
Python 代码:
class Solution:
def longestNiceSubstring(self, s: str) -> str:
n, idx, lenv = len(s), -1, 0
for i in range(n):
a, b = 0, 0
for j in range(i, n):
c = s[j]
if c.islower():
a |= (1 << (ord(c) - ord('a')))
else:
b |= (1 << (ord(c) - ord('A')))
if a == b and j - i + 1 > lenv:
idx, lenv = i, j - i + 1
return "" if idx == -1 else s[idx: idx + lenv]
-
时间复杂度: -
空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉