240927-一些常用卷积清晰易懂的blender动画展示(Conv、GConv、DWConv、1*1Conv、Shuffle)
在几个月前,写过一篇关于卷积过程中输入图像维度变化的博客240627_关于CNN中图像维度变化问题_图像的尺寸为什么又四个维度-CSDN博客,但是当时也是技术力不足,使用的是纯文字描述,可能对于初学者的帮助确实不大。机缘巧合下学习了blender,这次也有能力完善之前这篇博客。
一般来说涉及到的维度变换都是四个维度,当batch size=4,图像尺寸为640*640,RGB三通道时,此时维度就是4×3×640×640。3的意思是RGB三通道,如果你传入的图像是单通道图像,此时维度就是4×1×640×640。
当然有些图你看着是一个黑白图,但是他还是有可能是一张RGB三通道图,具体怎么区分呢。右击图片打开属性,打开详细信息,里面可以看到位深度,位深度为24,则为RGB图,位深度为8,则为单通道图。此处就是一个坑,图像分割任务中,标签往往是单通道图,但是有时从网上找到的数据集看起来是黑白的,但是实际训练就会报错,查看了才发现位深度是24,需要用python代码进行修改,具体跳转240627_图像24位深度(RGB图)转为8位深度(单通道图)-CSDN博客。
当维度是三维时,就是没有batch size这个维度,可以理解为这个维度指的是其中一张图。该文举例均为三维,因为三维是对其中一张图的处理,第四维是几就是几张图片,重复几次而已,无需重复赘述。
本文只展示维度上的推演计算,不展示数值的计算及代码展示。
因csdn上传图片大小限制,只能大刀砍画质和帧率,如不清晰及卡顿请谅解。(60帧压成4帧,1080p压成480p。太惨了)
注:图片没有添加任何水印,如需使用请标明出处。
标准卷积
首先我们以标准卷积为例
卷积输出的计算公式为
h e i g h t o u t = ( h e i g h t i n − h e i g h t k e r n e l + 2 ∗ p a d d i n g ) s t r i d e + 1 height_{out}=\frac{(height_{in}-height_{kernel}+2*padding)}{stride}+1 heightout=stride(heightin−heightkernel+2∗padding)+1
w i d t h o u t = ( w i d t h i n − w i d t h k e r n e l + 2 ∗ p a d d i n g ) s t r i d e + 1 width_{out}=\frac{(width_{in}-width_{kernel}+2*padding)}{stride}+1 widthout=stride(widthin−widthkernel+2∗padding)+1
此处我们输入1张7*7,8通道的图像(8×7×7),经过3×3卷积(padding=0,stride=1),此时的计算公式为
h
e
i
g
h
t
o
u
t
=
w
i
d
t
h
o
u
t
=
(
7
−
3
+
2
∗
0
)
1
+
1
=
5
height_{out}=width_{out}=\frac{(7-3+2*0)}{1}+1=5
heightout=widthout=1(7−3+2∗0)+1=5
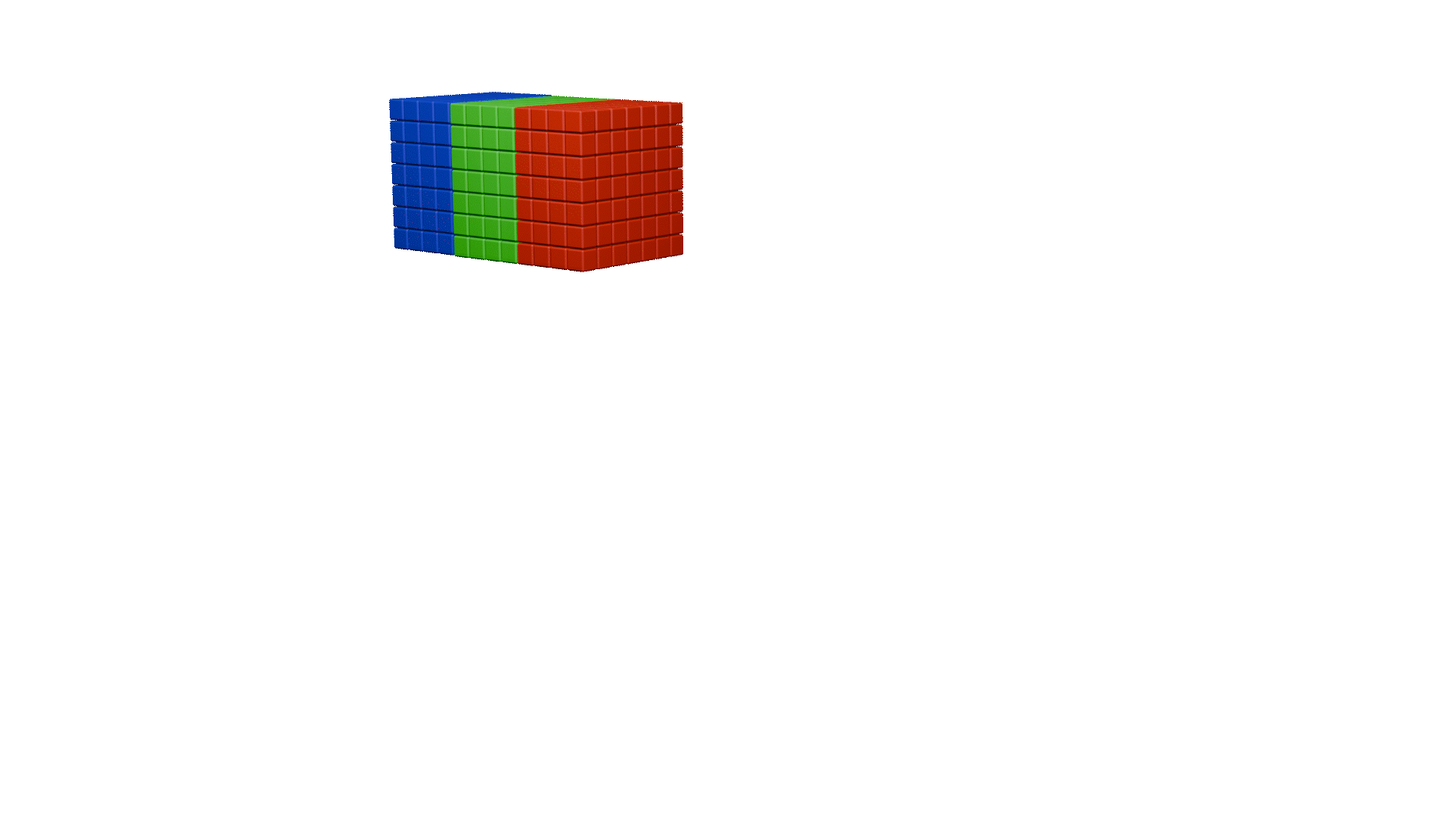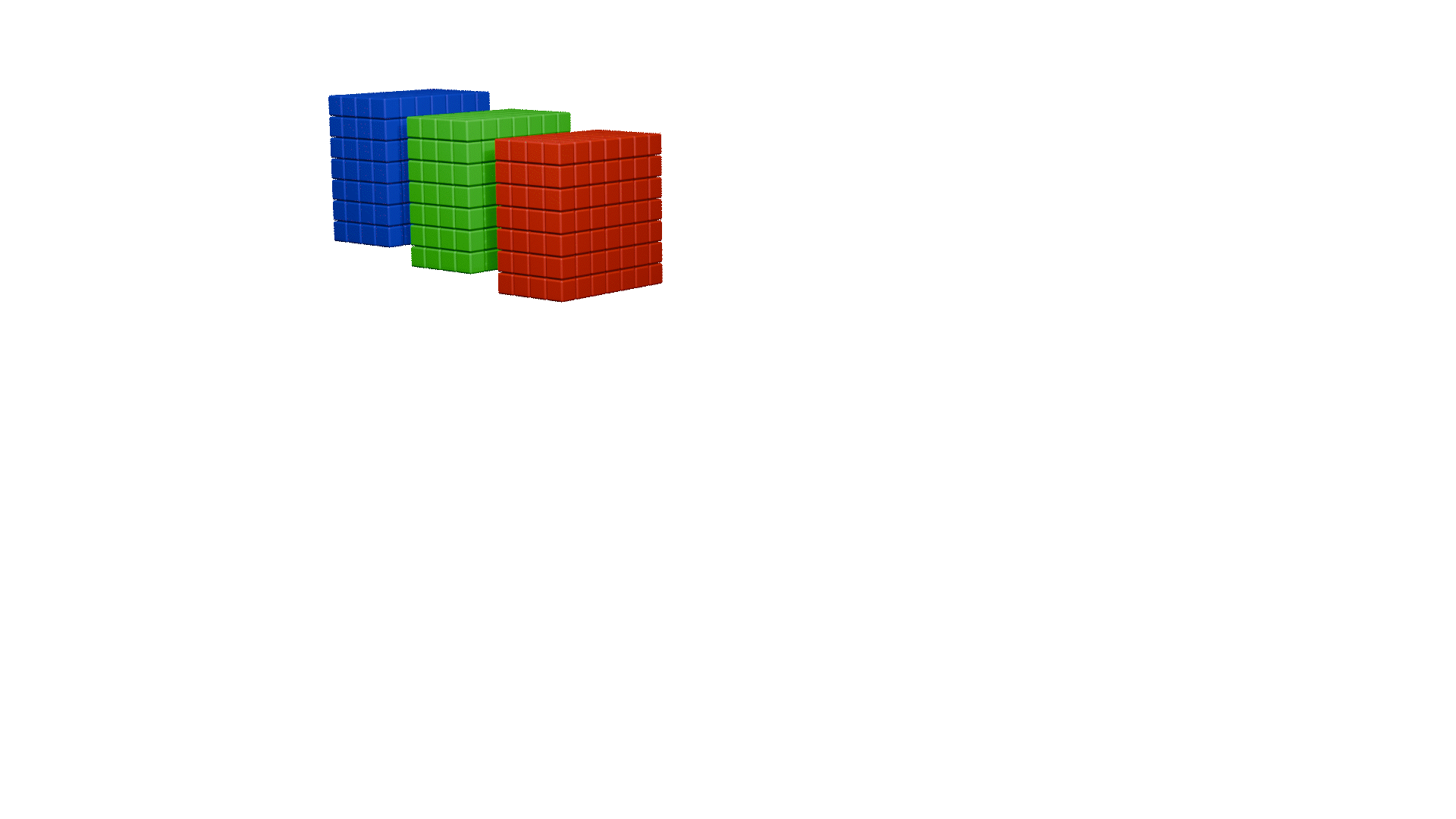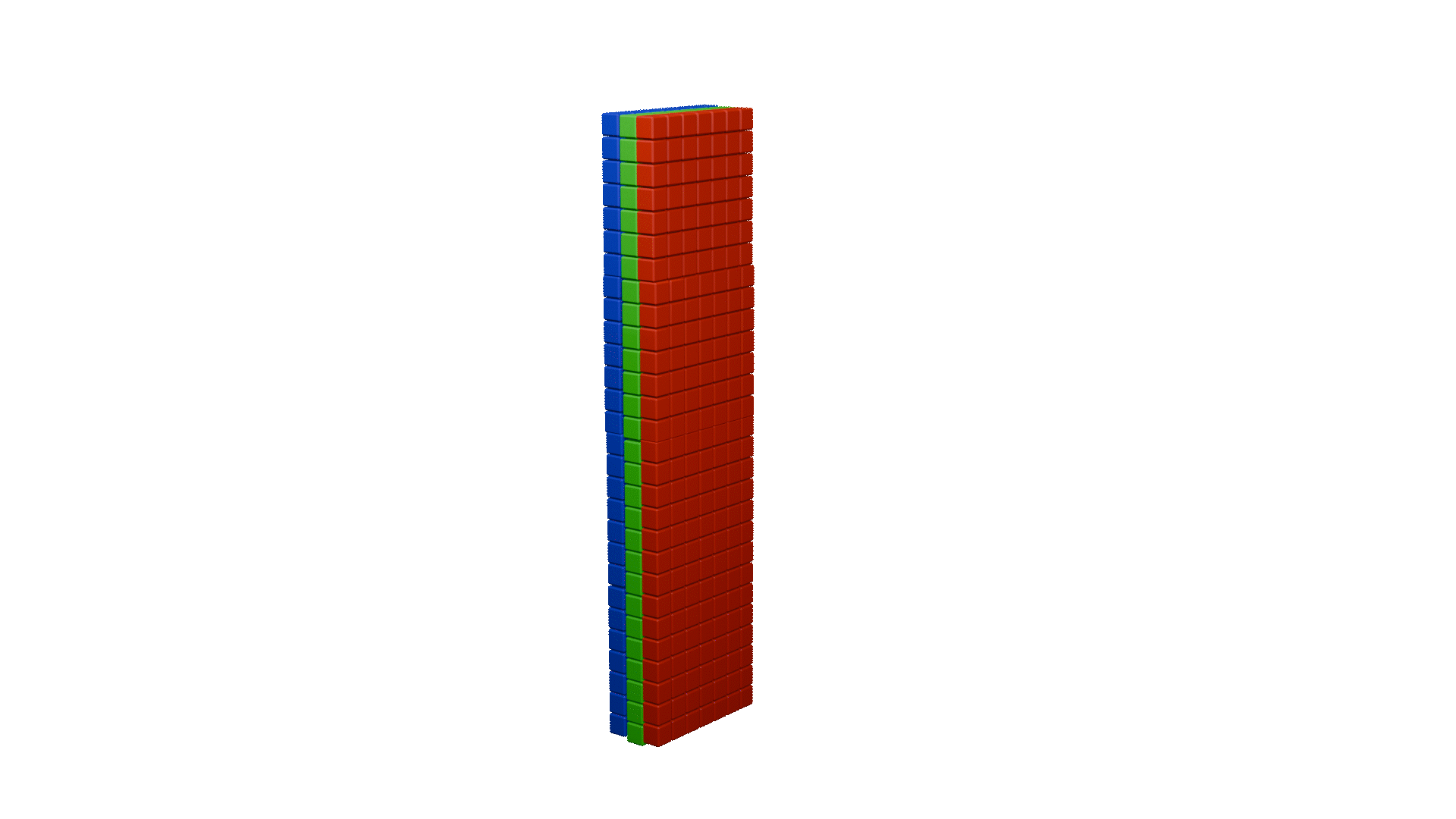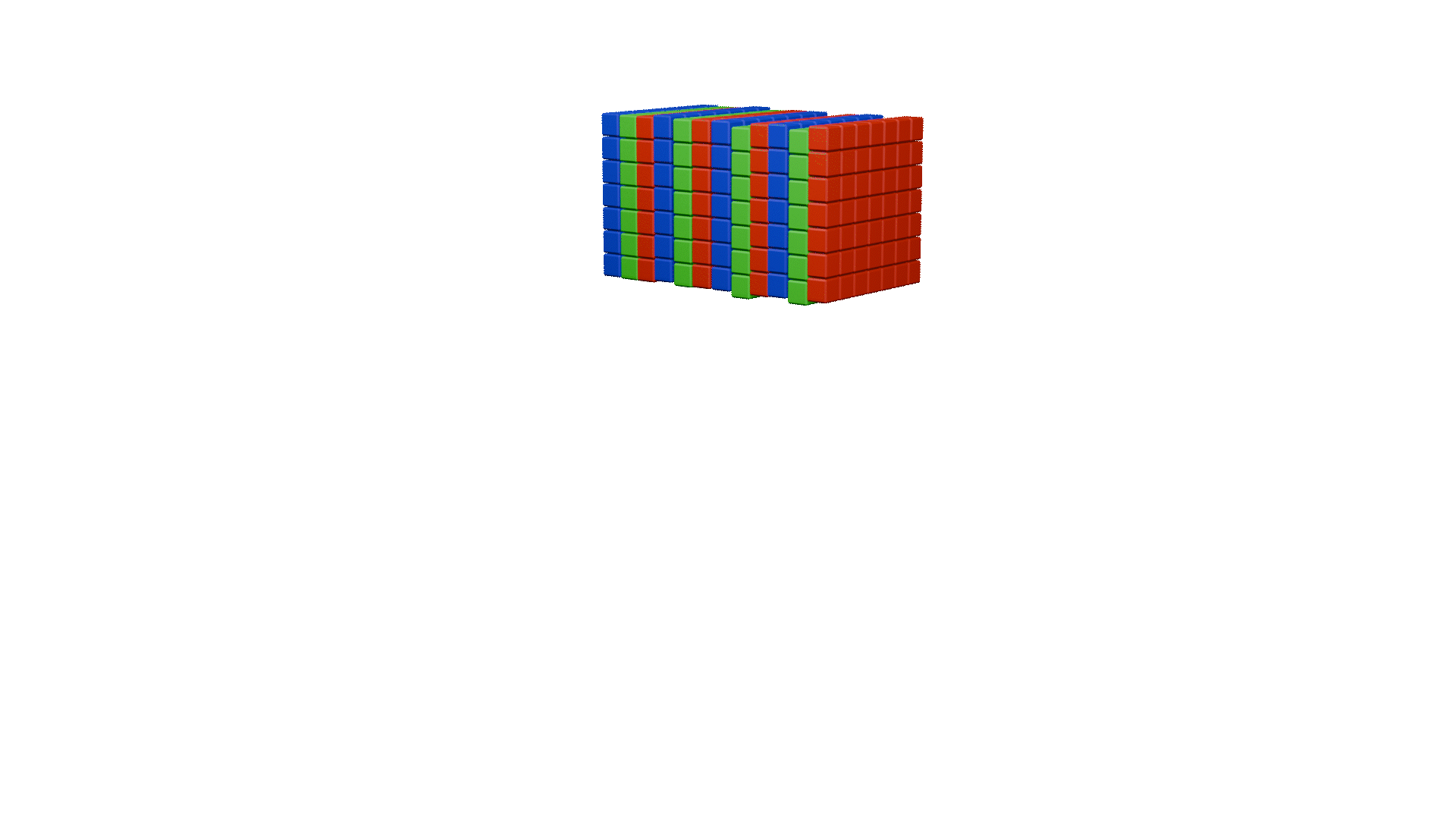
此处为便于演示,我们的卷积核数和输入图像通道数一致,都是8,所以输出图像维度为(8×5×5),如下动画所示:

注:图片没有添加任何水印,如需使用请标明出处。
| batch_size | height | width | in_channel | out_channel | |
|---|---|---|---|---|---|
| Input | 1 | 7 | 7 | 8 | |
| Kernel | 3 | 3 | 8 | 8 | |
| Output | 1 | 5 | 5 | 8 |
分组卷积
原论文:AlexNet《ImageNet Classification with Deep Convolutional Neural Networks》
最初是因为GPU算力不足,把卷积分组后放到不同的GPU中并行执行。分组后参数量为原来的1/g(g为分组数)
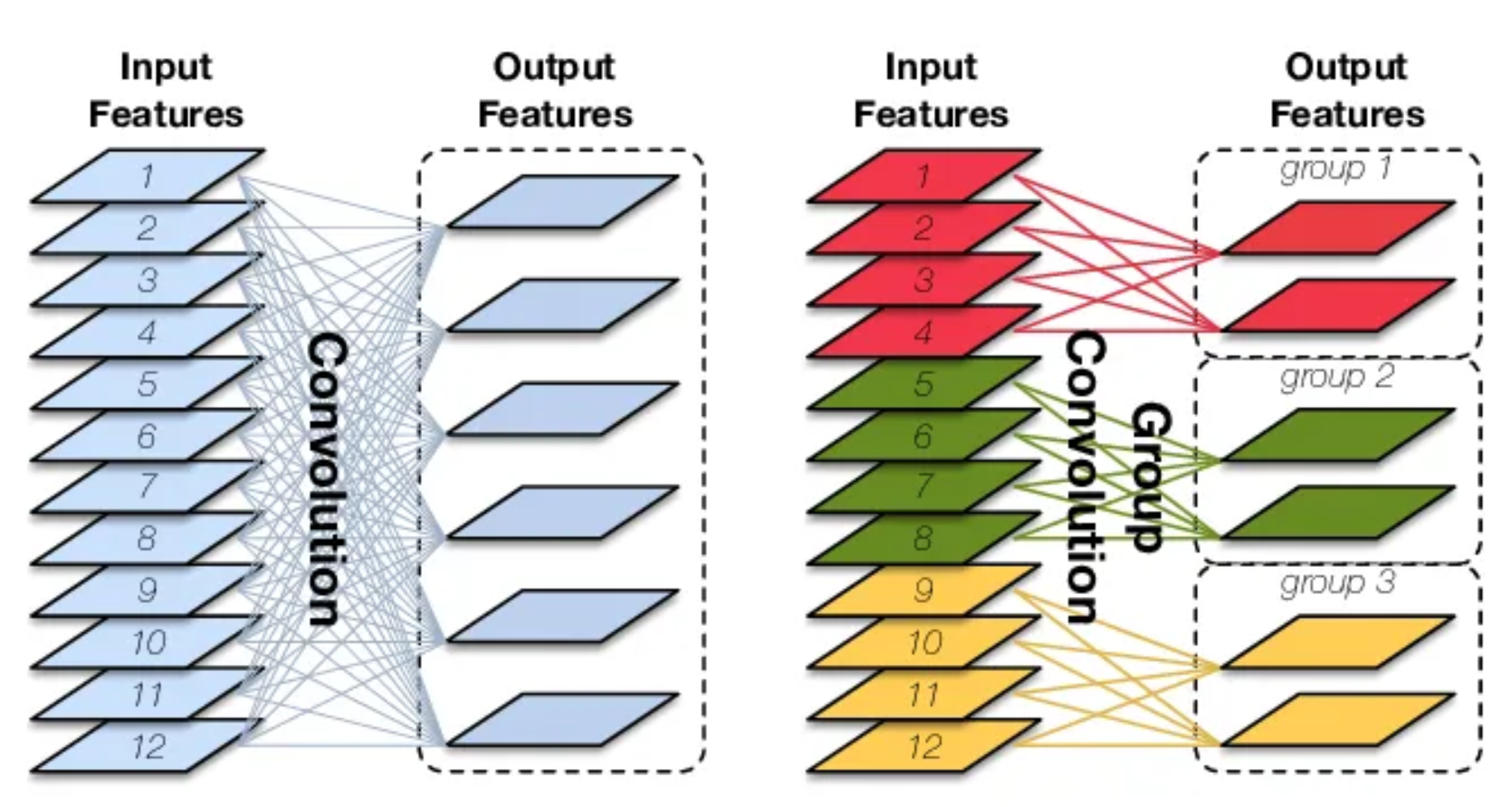
分组卷积中,卷积核和输入图像都被分为不同的组,其中有相互对应关系,每组卷积核和对应的输入channel进行卷积计算,最后将结果合并组合。
如下图,输入图像被分为两个组,同时也有两组卷积与之对应,第一组卷积负责处理前半部分,第二组卷积负责处理后半部分,最后将结果合并,如下动画所示。

注:图片没有添加任何水印,如需使用请标明出处。
深度可分离卷积
所谓深度可分离卷积,就是极致的分组卷积+逐点卷积。
原论文:《Xception: Deep Learning with Depthwise Separable Convolutions》
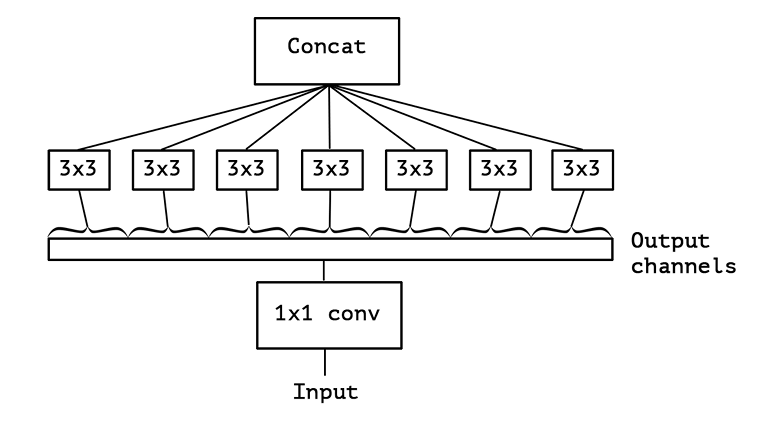
极致的分组卷积即输入的图像有多少个channel,我们就将其分成多少组,比如上面的组卷积中,我们输入的图是8channel的,我们这里就把他分成8个组,分别进行卷积,但这样也会产生一个很严重的问题,就是各组之间信息不流通。如下动画所示。
注:这里没有绘制出在输入图像上的滑动框,是因为分组数太多,会相互遮挡,画出来没有意义,实际是每个维度独立参与卷积运算,不是整个,例如第一层与第一个卷积核进行卷积,第二层与第二个卷积核进行卷积。

注:图片没有添加任何水印,如需使用请标明出处。
为了解决这个问题,需要使用1x1逐点卷积将深度卷积的输出按通道投影到一个新的特征图上。如下动画所示。

注:图片没有添加任何水印,如需使用请标明出处。
下面这个动画就是整个深度可分离卷积的动画。

注:图片没有添加任何水印,如需使用请标明出处。
逐点分组卷积
原论文:《ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices》
大量的1*1卷积会产生大量的计算量,计算成本昂贵,所以shufflenet提出了逐点分组卷积
所谓逐点分组卷积,就是在上述深度可分离卷积的基础上,再把深度卷积的结果进行分组,然后进行逐点卷积,可以对照上述深度可分离卷积动画查看。这里就没必要再单独做一个动画了。
channel shuffle
原论文:《ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices》
ShuffleNet除了提出逐点分组卷积之外,还提出了channel shuffle操作
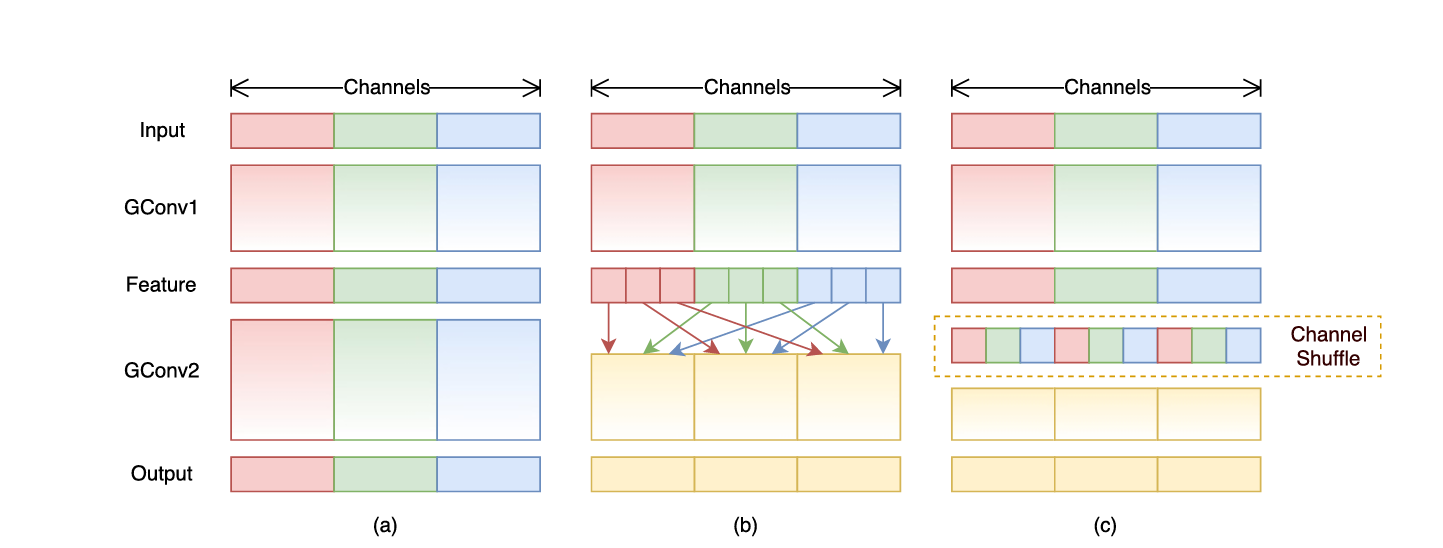
上图中a图代表了常规的分组卷积,可以看到每一组各自为战,相互之间没有战术交流(信息交流),最终输出的特征仅由一部分输出通道的特征计算得出,这种操作阻碍了信息的流通。我们就想,能不能把每一组的信息打乱,分散在不同组中,图b就是这样的设计思想。将每组的特征分散到不同的组后,在进行下一组卷积,但具体该如何实现呢,图c就是一种实现思路,这就是通道混洗。具体实现方法如下图所示:
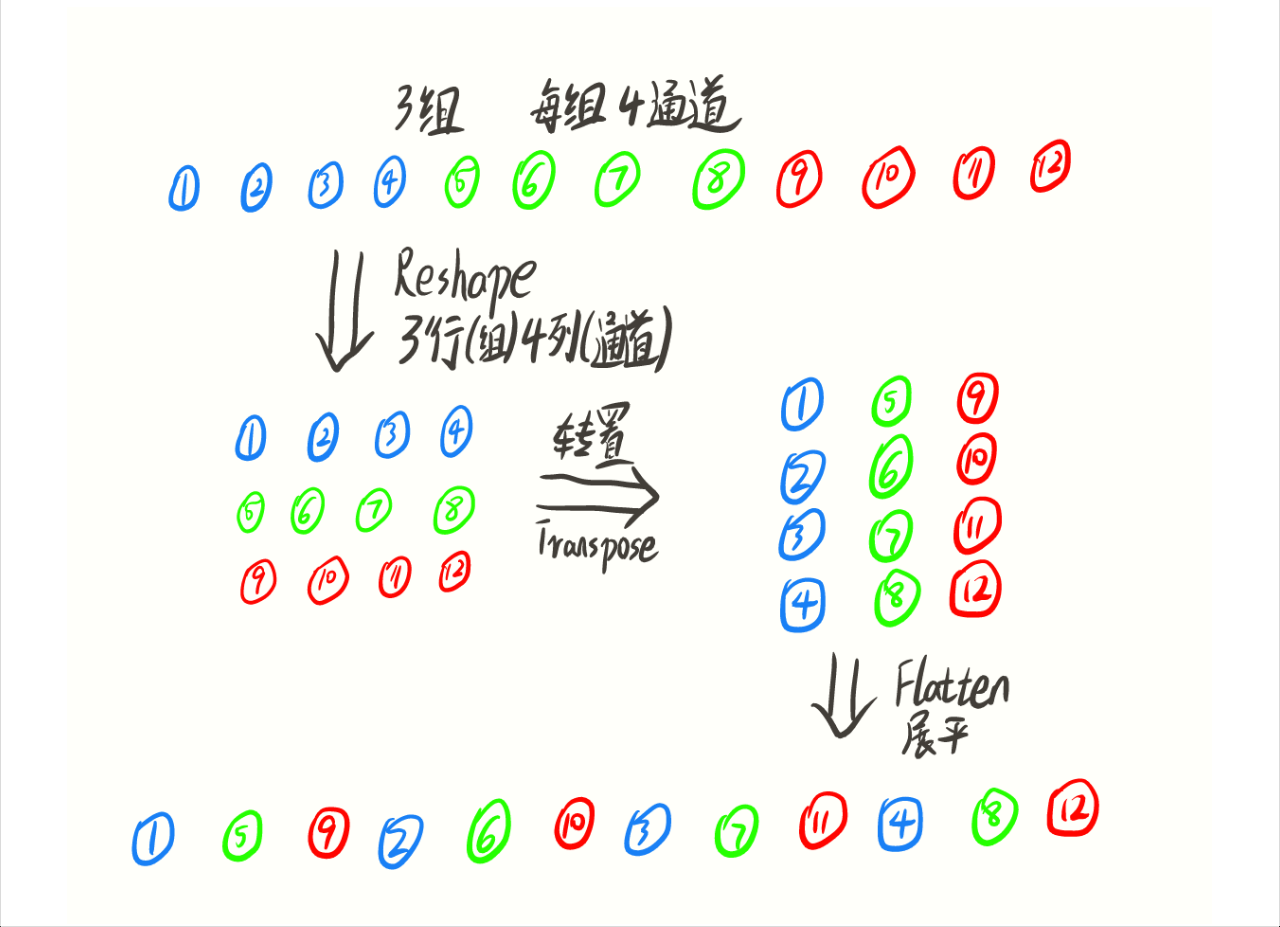
同样,这里也为大家做了动画展示:
Reference:
【图解AI:动图】各种类型的卷积,你认全了吗?_卷积运算过程示意图-CSDN博客
[一文看尽深度学习中的20种卷积(附源码整理和论文解读) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/381839221#:~:text=引言. 卷积,是卷积)
详述Deep Learning中的各种卷积(一) - 知乎 (zhihu.com)
ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices)
Network In Network)
Xception: Deep Learning with Depthwise Separable Convolutions)
ImageNet classification with deep convolutional neural networks (acm.org)
Net classification with deep convolutional neural networks (acm.org)](https://dl.acm.org/doi/pdf/10.1145/3065386)