文章出处:数据结构和算法之树形结构(3)
关注码农爱刷题,看更多技术文章!!
四、平衡二叉树(接前篇)
上一章节讲到为了避免二叉查找树退化成链表后的极度不平衡带来的低效率而衍生出了平衡二叉树,平衡二叉树的严格定义是这样的:二叉树中任意一个节点的左右子树的高度相差不能大于 1。这样的定义就是尽可能保证二叉树左右节点的平衡,从而保证时间复杂度的高效。从平衡二叉树的定义不难看出,不仅满二叉树,还有完全二叉树(关于两者的定义,可以查看前述文章 数据结构和算法之线性结构)都是符合平衡二叉树定义的,而其他的非完全二叉树也可能是平衡二叉树,例如下图就是一棵非完全二叉树,但它是平衡二叉树。
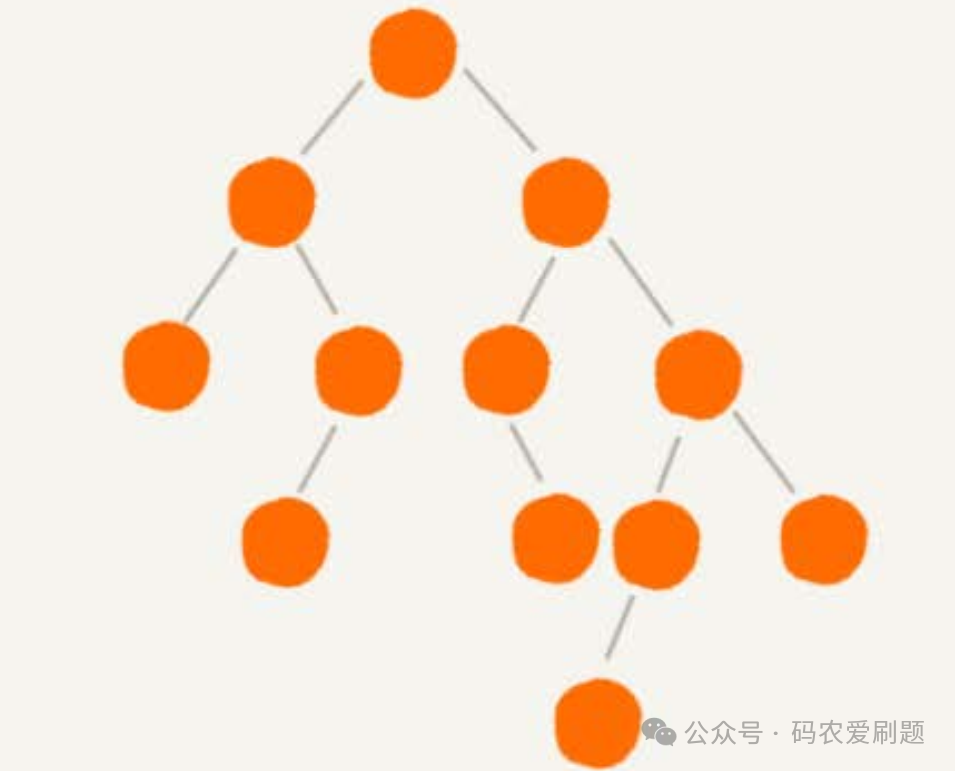
了解平衡二叉树基本定义后,我们再看平衡二叉查找树,所谓平衡二叉查找树就是不仅要满足平衡二叉树的定义,还需要满足二叉查找树的规范即按大小排序。常见的平衡二叉查找树有AVL树和红黑树,本章先介绍AVL树。
五、AVL树
AVL树是最早设计出来的一种平衡二叉查找树,它通过在插入和删除节点时进行旋转操作来保持内部树的平衡,即任何节点的左右子树高度相差不超过1,是一种严格的自平衡二叉树。这种即时的高度自平衡机制是AVL树最大的特点,也使得其在执行查找、插入和删除操作时的效率非常高,其时间复杂度保持在O(log n)。
AVL树自平衡机制
要了解AVL树的自平衡机制,我们要先了解一些基本概念:
平衡因子:即AVL树每个节点都有一个平衡因子,定义为其左子树的高度减去右子树的高度;平衡因子的值只能是-1、0或1。通俗的说,平衡因子就是AVL树节点的左右子树高度的差的负值,如果左子树比右子树高一层,那么平衡因子就为-1;如果左右子树一样高,平衡因子就为0;如果右子树比左子树高一层,那么平衡因子就为1,这三种情况下AVL树的性质都没有被打破。按照这个规则,如果平衡因子为-1到1以外的其他值,则说明左右子树已经失衡,AVL树性质被打破,AVL树则不再是一棵AVL树。而对AVL树进行增删节点,就会破坏这种平衡即失衡,所以AVL树引进了一种机制,在增删节点后,通过节点自旋来恢复被破坏的平衡性,这种机制即AVL树的自平衡机制。所谓节点自旋,就是在不改变AVL树节点大小顺序的情况下调整树的结构使之重新平衡(这个平衡本质上就是其左右子树高度的平衡)。
对于AVL树失衡的四种场景和对应的旋转方式总结如下表:

LL场景-右旋
下面我们以LL场景为例,对AVL树失衡和通过旋转实现自平衡的过程进行说明。所谓LL失衡,即节点左子树高度大于右子树高度且高差大于1,并且其左子节点的左子树也高于或等于右子树的高度但差在平衡因子值正常范围内,如下图:
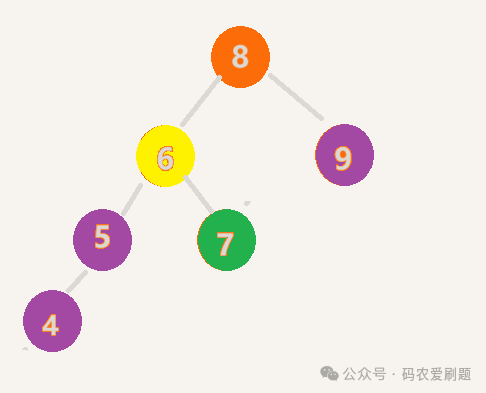
图中根节点8左子树高度-右子树高度 = 2,即失衡;而其左子节点6左子树高度也高于右子树高度但高度差为1。调整的旋转方法则向相反方向旋转,即右旋,具体步骤如下:
1. 右旋失衡根节点8使其成为其左节点6的右节点;2. 同时使原左节点6的右孩子7成为原根节点8的左节点
旋转后的图如下,旋转后,恢复了AVL树的平衡特性:
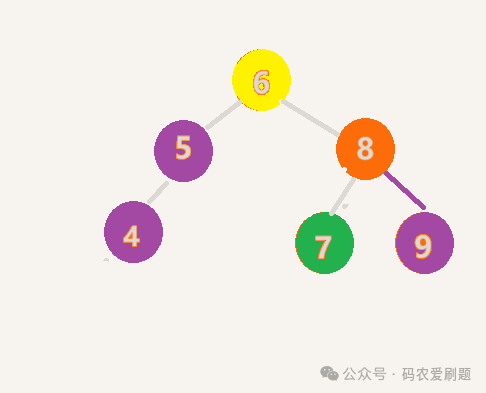
左旋过程类似,右旋和左旋实现代码如下:
private AVLNode rightRotate(AVLNode red) {
AVLNode yellow = red.left;
AVLNode green = yellow.right;
yellow.right = red;
red.left = green;
return yellow;
}
private AVLNode leftRotate(AVLNode red) {
AVLNode yellow = red.right;
AVLNode green = yellow.left;
yellow.left = red;
red.right = green;
return yellow;
}LR场景-左右旋
下面我们再用稍微复杂的RL场景为例,对AVL树失衡和通过旋转实现自平衡的过程进行进一步说明。所谓LR失衡,即失衡节点左子树高度大于右子树高度且高差大于1,并且失衡节点左子节点的右孙子树高于左孙子树的高度但差在平衡因子值正常范围内,如下图:
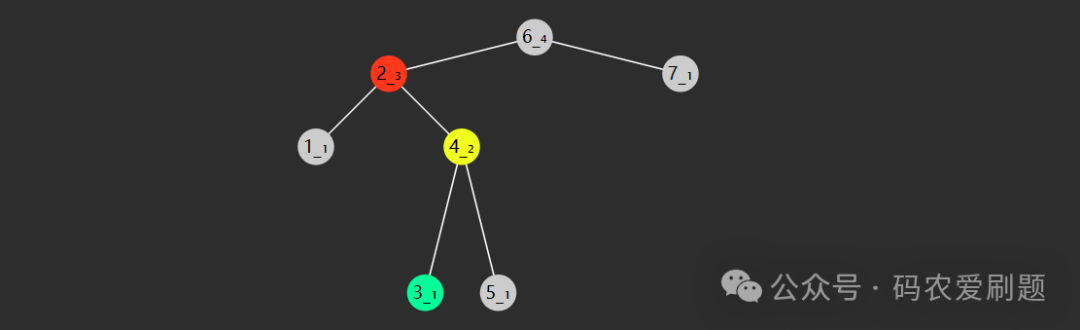
图中根节点6左子树高度-右子树高度 = 2,即失衡;而其左子节点6的右孙子树高于左孙子树且高度差为1。调整的旋转方法则采用左右旋,具体步骤如下:
1. 先左旋左节点2,使其右孩子4成为其父节点;同时右孩子4成为根节点6的左节点,操作完后如下图:
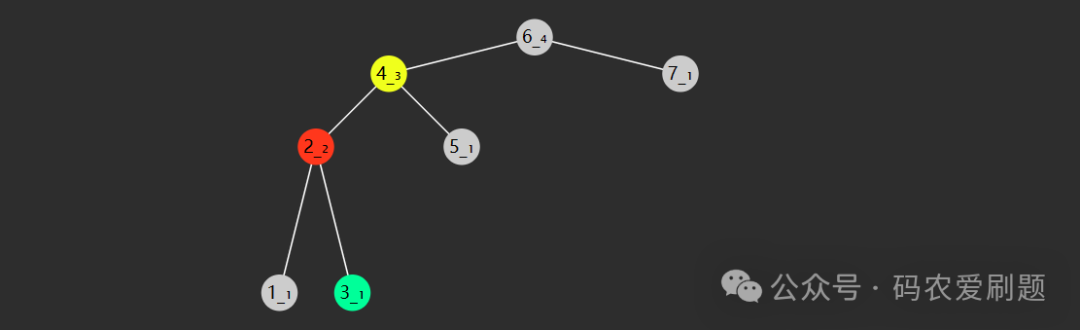
2. 再右旋根节点6,使其成为左节点4的右节点;同时,左节点4成为新的根节点,而节点5则成为原根节点6的左节点
左右旋转都完成后图如下:

其实,LR场景就是RR场景和LL场景的组合,第一步左旋后,LR场景就从RR场景转变为了LL场景,所以后续的处理也对应LL场景处理方法右旋即可,这点从代码实现上也可以看出:
private AVLNode leftRightRotate(AVLNode root) {
root.left = leftRotate(root.left); // 先左旋左节点,对应RR
return rightRotate(root); // 再右旋根节点 对应LL
}
private AVLNode rightLeftRotate(AVLNode root) {
root.right = rightRotate(root.right);
return leftRotate(root);
}RL场景的右左旋,逻辑则刚好相反,大家可自行去研究,AVL树的自平衡机制和相关知识就介绍到此(其节点增删查找同二叉查找树一致,此处也不再重复介绍,可参看前述文章)。正由于AVL树的自平衡机制,使AVL树能持续保持平衡二叉树的特性,从而能保证其时间复杂度一直接近O(logN),且处理旋转的时间复杂度为O(1),因而整体上会比非平衡二叉查找树有更好的效率。
但是成也萧何、败也萧何,AVL树的优点在某些场景下也会变成缺点,例如在大规模节点频繁插入和删除的场景下,实现自平衡机制的旋转操作就会成为负担,所以,红黑树应运而生。红黑树相关知识,请关注后续章节。
码农爱刷题
为计算机编程爱好者和从业人士提供技术总结和分享 !为前行者蓄力,为后来者探路!