目录

题目描述：

思路：

具体实现

整体建立一个大小为N的小根堆

通过大根堆实现

完整代码

---

力扣链接：面试题 17.14. 最小K个数 - 力扣（LeetCode）

题目描述：

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例：

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

思路：

这个问题属于是一类问题中，即top-K问题：N个数据中，前k个最大/最小的元素，一般来说k比较小；或者是需要找到这组数据中 第k大/第k小 的数据。

根据这道的要求，我们可以有以下三种思路：

1. 整体排序
2. 整体建立一个大小为N的小根堆
3. 把前K个元素创建为大根堆，遍历剩下的N-K个元素，和堆顶元素比较，如果比堆顶元素学校，则堆顶元素删除，但前元素入堆

具体实现

整体建立一个大小为N的小根堆

通过创建一个小根堆，把要全部元素都放进去，然后再把前k个元素提出来即可。

class Solution {
    public int[] smallestK(int[] arr, int k) {
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        for(int i = 0; i < arr.length; i++){
            priorityQueue.offer(arr[i]);
        }

        int[] ret = new int[k];
        for(int i = 0; i < k; i++){
            ret[i] = priorityQueue.poll();
        }

        return ret;
    }
}

由PriorityQueue创建的堆默认为小根堆，所以把元素直接放进去，priorityQueue会默认成为小根堆，然后再把前k个元素放到ret数字里即可。

通过大根堆实现

这里有一个要做的地方：让PriorityQueue可以实现大根堆。

 通过 按住Crtl 鼠标点击 PriorityQueue 可以看到其中实现的方法，

再Crtl  鼠标点击 Comparator，看Comparator接口中的方法，

可以看到其中有个 compare方法，这便是通过比较 o1，o2的值来进行小根堆的实现，这里我们可以通过重写compare方法来实现大根堆。这里选择的是创建一个新类来实现。

class IntCmp implements Comparator<Integer> {

    @Override
    public int compare(Integer o1, Integer o2) {
        return o2.compareTo(o1);
    }
}

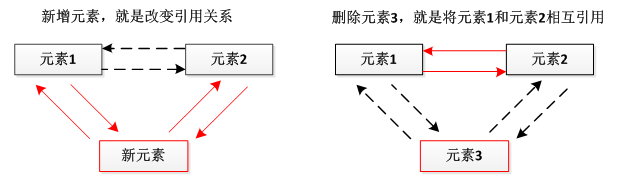
然后把前K个元素放进大根堆，如果根节点的值大于可能要放进来的值，则把根节点删除，把该值放进来，同时PriorityQueue会保证该堆一直为大根堆。最后遍历完N-K个值后，再把这些值返回出去。

其中的过程大概如上图所示。

class Solution{
    public int[] smallestK(int[] arr, int k) {
    int[] ret = new int[k];
    if(arr == null || k == 0) return ret;
    PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new IntCmp());

    for (int i = 0; i < k; i++) {
        priorityQueue.offer(arr[i]);
    }

    for (int i =k; i < arr.length; i++) {
        int peekVal = priorityQueue.peek();
        if(peekVal > arr[i]) {
            priorityQueue.peek();
            priorityQueue.offer(arr[i]);
        }
    }

    for (int i = 0; i < k; i++) {
        ret[i] = priorityQueue.poll();
    }
    return ret;
    }
}

完整代码

第一种方法，通过小根堆实现

//时间复杂度为：O((k+1)logN)
class Solution {
    public int[] smallestK(int[] arr, int k) {
                PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        //时间复杂度为O(N*logN)
        for (int i = 0; i < arr.length; i++) {
            priorityQueue.offer(arr[i]);
        }
        
        //时间复杂度为O(K*logN)
        int[] ret = new int[k];
        for (int i = 0; i < k; i++) {
            ret[i] = priorityQueue.poll();
        }
        
        return ret;
    }
}

第二种方法，通过大根堆实现

class IntCmp implements Comparator<Integer> {

    public int compare(Integer o1, Integer o2) {
        return o2.compareTo(o1);
    }
}

class Solution{
    public int[] smallestK(int[] arr, int k) {
    int[] ret = new int[k];
    if(arr == null || k == 0) return ret;
    PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new IntCmp());

    for (int i = 0; i < k; i++) {
        priorityQueue.offer(arr[i]);
    }

    for (int i =k; i < arr.length; i++) {
        int peekVal = priorityQueue.peek();
        if(peekVal > arr[i]) {
            priorityQueue.peek();
            priorityQueue.offer(arr[i]);
        }
    }

    for (int i = 0; i < k; i++) {
        ret[i] = priorityQueue.poll();
    }
    return ret;
    }
}