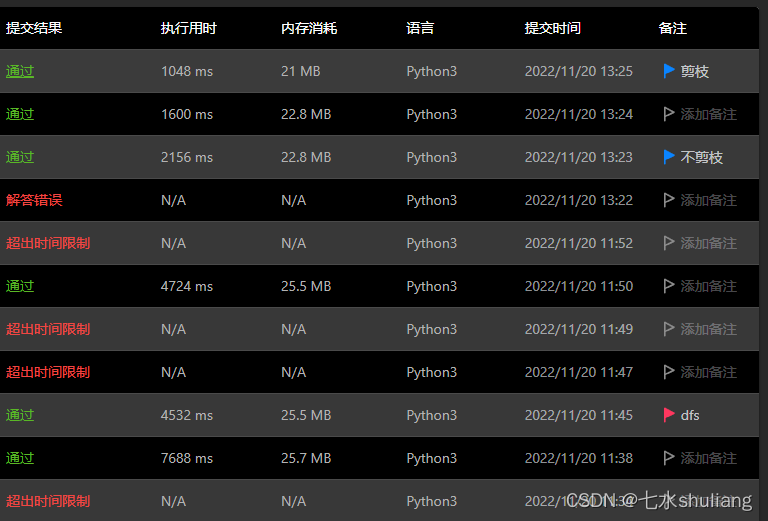
一、本周周赛总结

• T4写了N^3，估计会被re，哭了。
• T2 dfs+二分。
• T3 dfs树状dp。
• T4 dp+前缀和优化。
  

二、 [Easy] 6241. 数组中不等三元组的数目

链接: 6241. 数组中不等三元组的数目

1. 题目描述

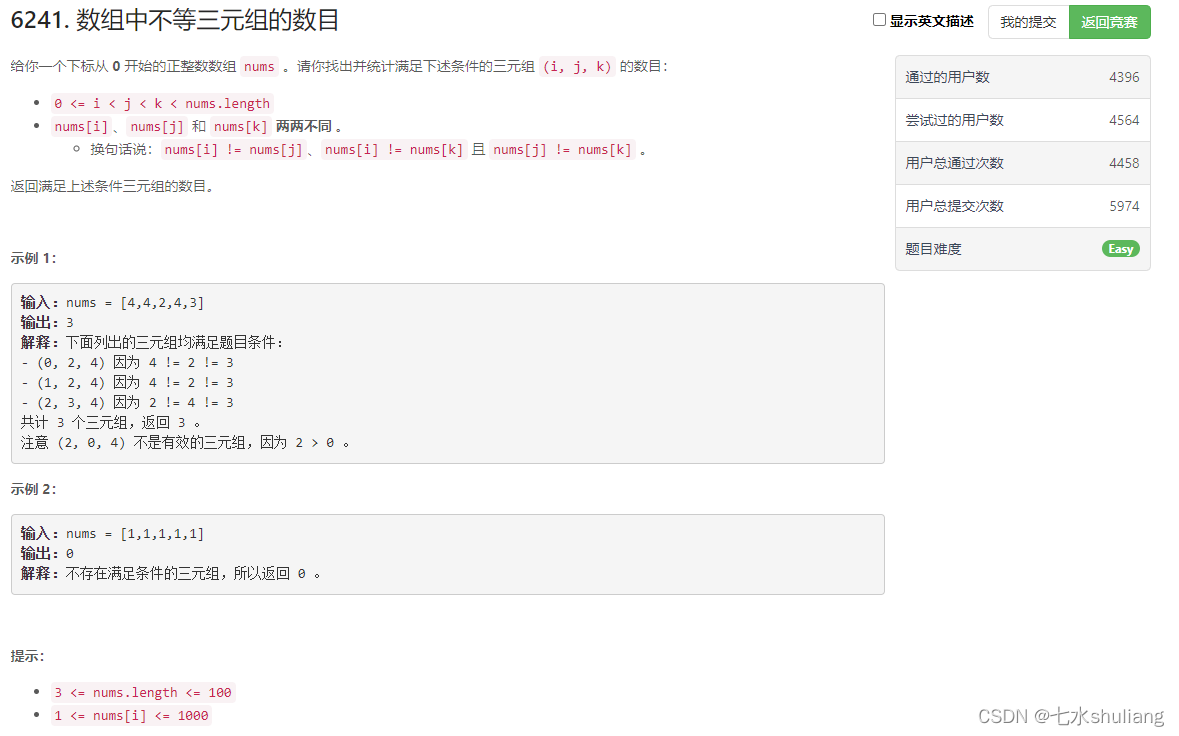
2. 思路分析

数据量100显然暴力模拟。

• 如果数据量大，可以采取排序然后枚举每个数作为中间数的方法，乘法原理乘三部分的数量。复杂度nlgn

3. 代码实现

class Solution:
    def unequalTriplets(self, nums: List[int]) -> int:
        n = len(nums)
        ans = 0
        for i in range(n-2):
            for j in range(i+1,n-1):
                for k in range(j+1,n):
                    if len({nums[i],nums[j],nums[k]}) == 3:
                        ans += 1
        return ans

三、[Medium] 6242. 二叉搜索树最近节点查询

链接: 6242. 二叉搜索树最近节点查询

1. 题目描述

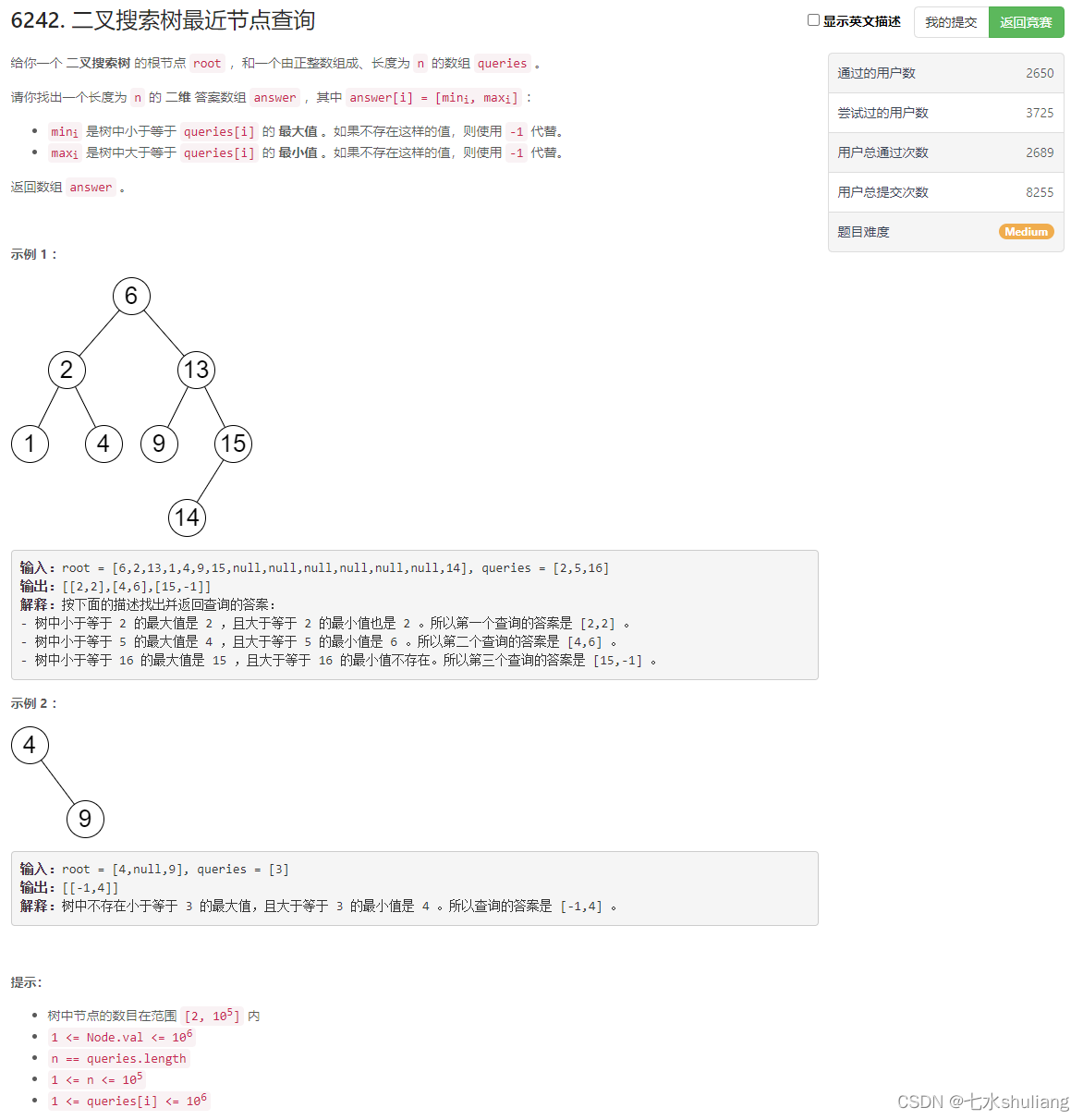
2. 思路分析

• 遍历出来二分即可。
• 没注意到题目是BST，实际上中根遍历后就是有序的。

3. 代码实现

class Solution:
    def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:
        a = set()
        def dfs(o):
            if not o:
                return 
            a.add(o.val)
            dfs(o.left)
            dfs(o.right)
        dfs(root)
        a = sorted(a)
        n = len(a)
        ans = []
        for x in queries:
            p = bisect_left(a,x)
            if p<n:
                if a[p] == x:
                    ans.append([x,x])
                    continue
                if p:
                    ans.append([a[p-1],a[p]])                    
                else:
                    ans.append([-1,a[p]])
            else:
                ans.append([a[-1],-1])
        return ans                                       

四、[Hard] 6243. 到达首都的最少油耗

链接: 6243. 到达首都的最少油耗

1. 题目描述

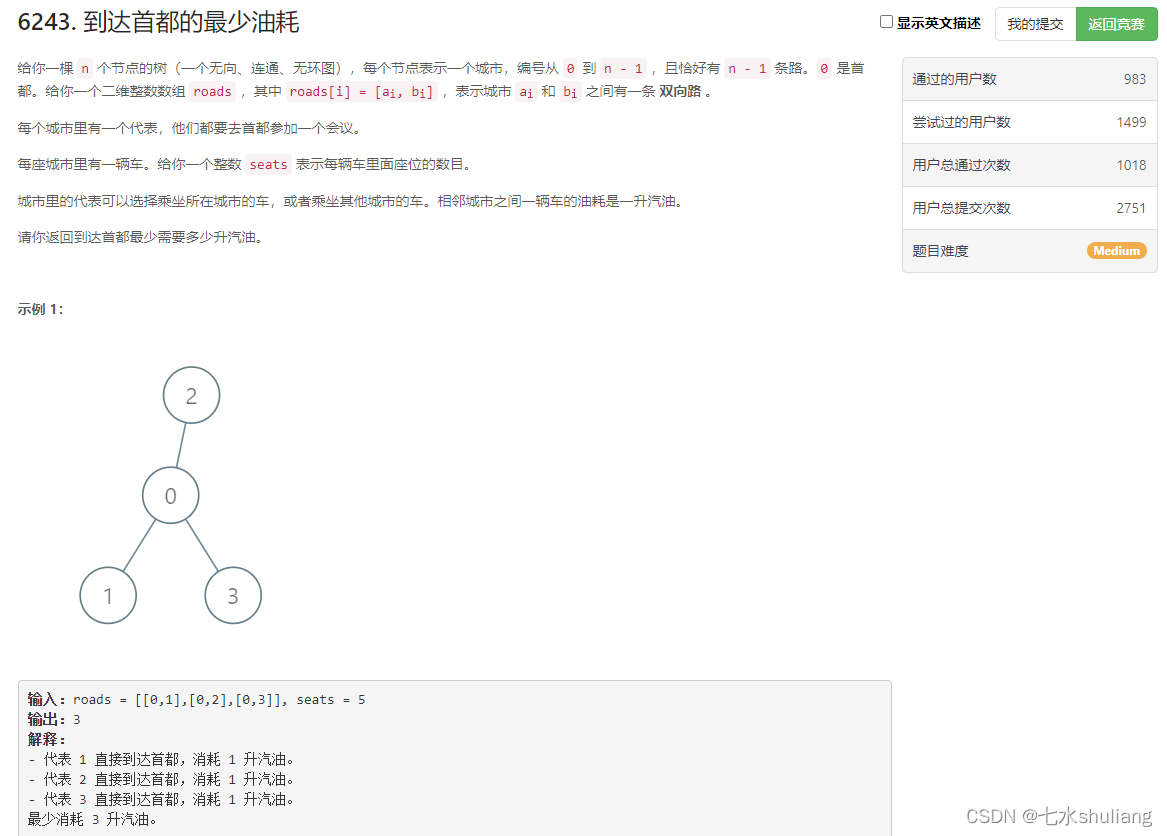
2. 思路分析

• 题目没说清楚，没想到可以换车。wa了一发。
• 由于可以换车，因此dfs时，每个节点的总人数除以座位数上取整就是车的数目。

3. 代码实现

class Solution:
    def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
        n = len(roads) + 1
        if  n == 1:
            return 0
        g = [[] for _ in range(n)]
        for u,v in roads:
            g[u].append(v)
            g[v].append(u)
        
        def dfs(u,fa):  # 载人数，油耗,车数
            s,cost,car = 0,0,0
            for v in g[u]:
                if v == fa:continue
                a,b,c= dfs(v,u)
                # print(u,v,a,b,c)
                s += a
                cost += b
                car += c
            if u == 0:
                return s,cost,car
            if s > 0:
                s += 1
                car = (seats+s-1)//seats
                
                return s,cost+car,car
            
            return s + 1,cost+car+1,car+1
        
        s,cost,car = dfs(0,-1)
            
        return cost

五、[Medium] 6244. 完美分割的方案数

链接: 6244. 完美分割的方案数

1. 题目描述

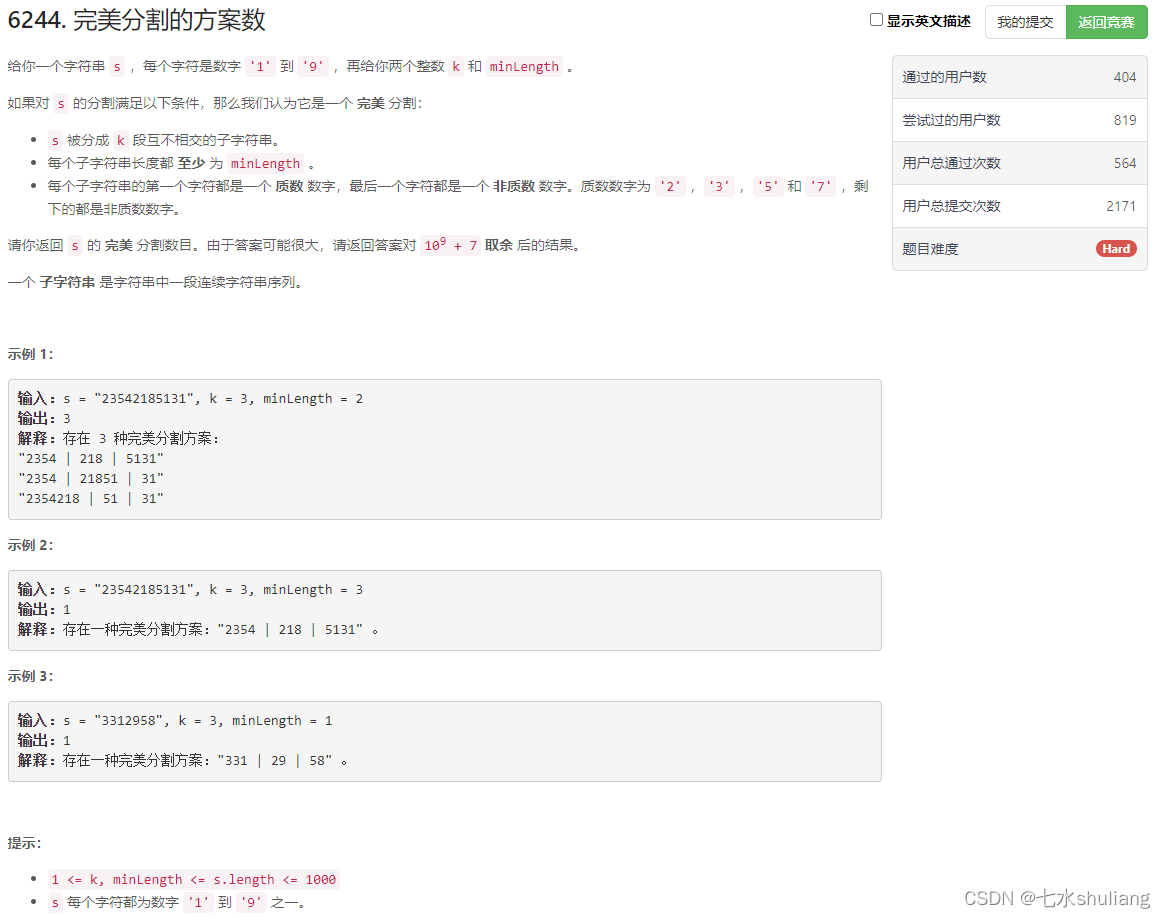
2. 思路分析

• 有取模，有方案数，有k段，显然是dp。
• 定义f[i][j]为s前j个数分成i段的情况。
• 这里注意段数i在外侧，这样才能前缀和优化。
• 正常的转移显然是n^3的，因为要遍历最后一段的分割点在哪，即f[i][j] = sum{f[i-1][j’]},其中j’是所有分割点，且j’+1到j是一段合法串，j’之前也是合法串。
• 这里需要前缀和优化，j向右遍历时，发现j’也是向右的，且不会用到之前的状态，只会用最后一个的状态，因此可以前缀和累计即可。
• 代码实现时，由于合法串可以用边界位置是否能分割来判断，可以写一个判断是否是合法分割点的函数来封装，以减少代码。
• 计算j时，可以剪枝前后的遍历边界位置。
  

3. 代码实现

MOD = 10**9+7
class Solution:
    def beautifulPartitions(self, s: str, k: int, minLength: int) -> int:
        n = len(s)
        ps = {2,3,5,7}
        a = list(map(int,s))
        def is_prime(v):
            return v in ps 
        def can_split(j):
            return j == 0 or j == n or (not is_prime(a[j-1]) and is_prime(a[j]))
        if k*minLength > n or is_prime(a[-1]) or not is_prime(a[0]):
            return 0
        f = [[0]*(n+1) for _ in range(k+1)]
        f[0][0] = 1
        for i in range(1,k+1):
            s = 0
            for j in range(minLength*i,n-(k-i)*minLength+1):
                if can_split(j-minLength):
                    s = (s+f[i-1][j-minLength])%MOD
                if can_split(j):
                    f[i][j] = s
                    
        return f[-1][-1]%MOD                               

考试时的n^3写法

MOD = 10**9+7
class Solution:
    def beautifulPartitions(self, s: str, k: int, minLength: int) -> int:
        n = len(s)
        ps = {2,3,5,7}
        if n < minLength:
            return 0
        if int(s[0]) not in ps:
            return 0
        if int(s[-1]) in ps:
            return 0
        a = list(map(int,s))
        # print(a)
        pp = [-1]
        for i in range(1,n-2):
            if a[i] not in ps and a[i+1] in ps:
                pp.append(i)
        if minLength<=2:
            return comb(len(pp)-1,k-1)%MOD
        # print(pp)
        @cache
        def f(i,j):
            if i == j == 0:
                return 1
            if i == 0:
                return 0
            if j <= 0:
                return 0
            # if a[i-1] in ps:
            #     return 0
            ret = 0
            pos = bisect_right(pp,i-minLength-1)
            for kk in range(0,pos):
                ret = (ret+f(pp[kk]+1,j-1))%MOD
            # for p in pp:
            #     if i-1-p>=minLength:
            #         # print(p+1,j-1,f(p+1,j-1))
            #         ret = (ret+f(p+1,j-1))%MOD
            return ret
            
        ans = f(n,k)%MOD        
        f.cache_clear()                       
        return ans

六、参考链接