Voxel mamba ：基于Mamba的3D目标检测算法解析

news2024/9/27 7:24:48

1 算法简介
- - 1.1 前提补充
  - - 空间填充曲线（Space-filling Curve）
    - 点云分组
2 模块介绍
- - 2.1 希尔伯特输入层（Hilbert Input Layer）
  - 2.2 双尺度 SSM 模块（Dual-scale SSM Block）
  - 2.3 隐式窗口分区（Implicit Window Partition）
  - 2.4 Voxel Mamba Backbone
  - 2.5 有效感受野 Effective Receptive Field of Voxel Mamba

github链接： https://github.com/gwenzhang/Voxel-Mamba/tree/master
参考链接： https://www.bilibili.com/read/cv35707685/

1 算法简介

背景：传统的基于序列化方法的三维体素（voxel）在输入到 Transformer 前会牺牲体素的空间邻近性，这限制了模型的性能。
Voxel Mamba：提出了一种无组（group-free）策略，将整个体素空间序列化为单一序列，减少了空间邻近性的损失。
Dual-scale SSM Block：提出了一种双尺度状态空间模块，通过建立层次结构来增强模型的接收域。
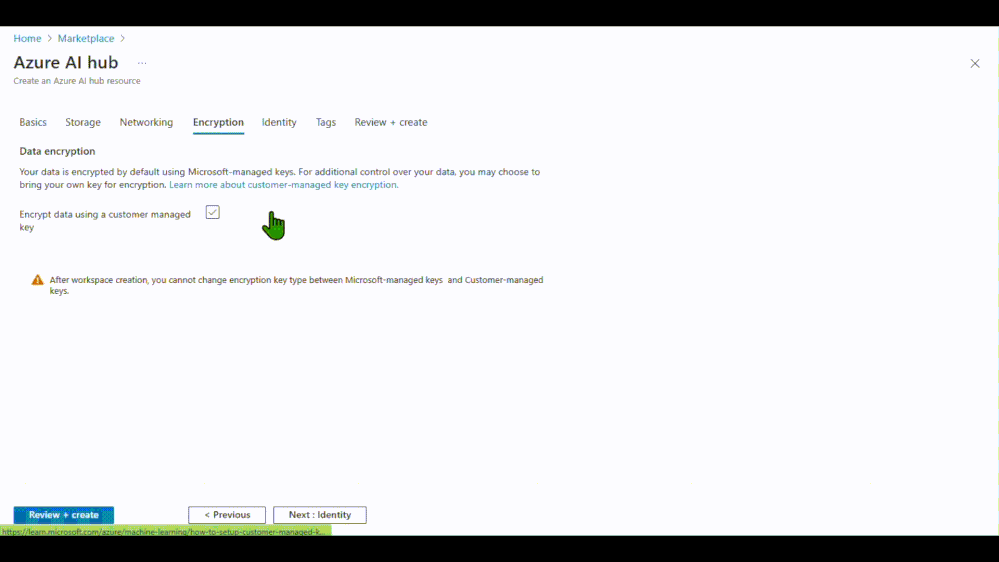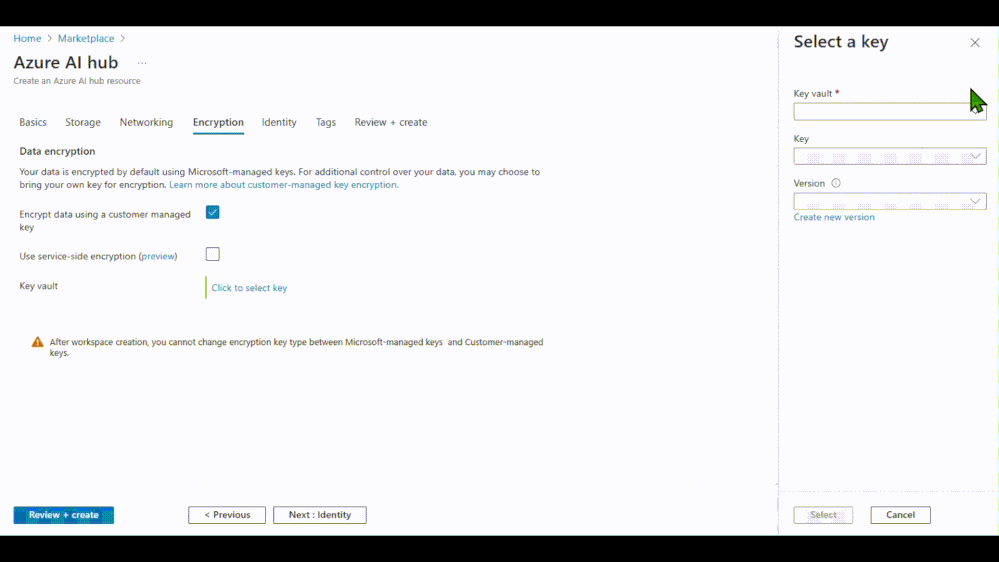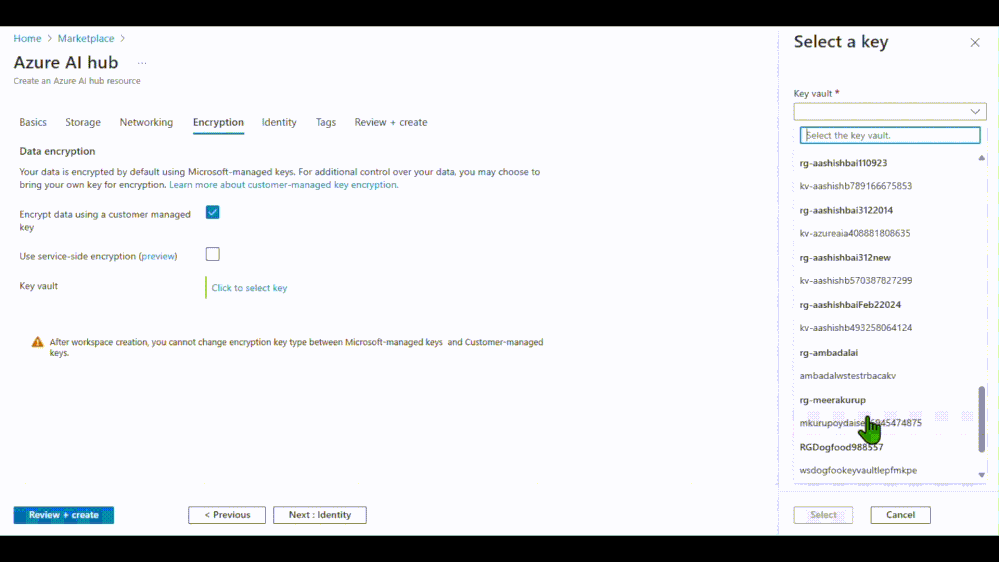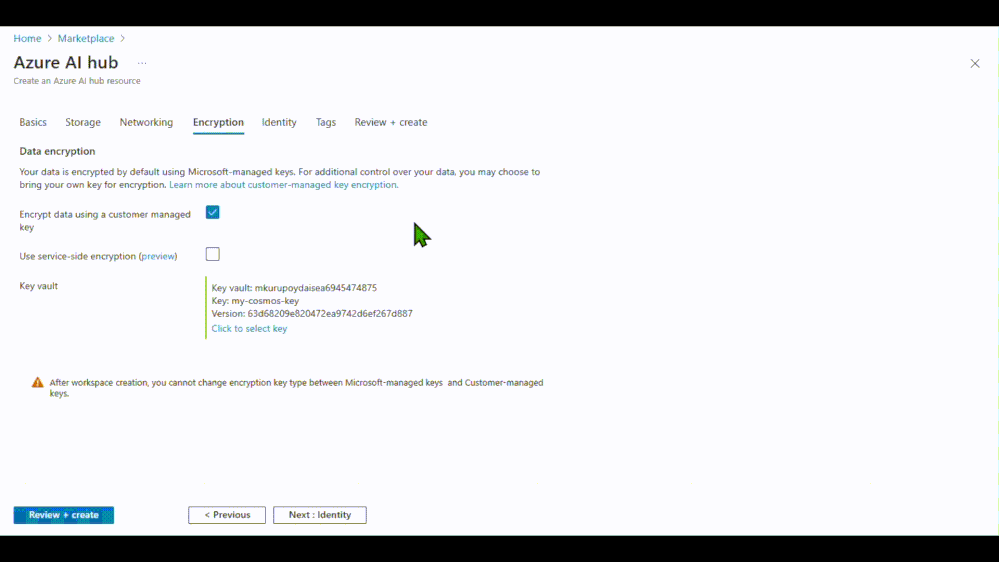
Implicit Window Partition：隐式窗口划分通过位置编码增强空间邻近性，无需显式进行空间窗口划分。

在这里插入图片描述

1.1 前提补充

空间填充曲线（Space-filling Curve）

空间填充曲线是一系列分形曲线，可以不重复地穿过多维空间中的每个点。经典的空间填充曲线包括希尔伯特曲线、Z阶曲线和扫描曲线等。这些方法可以在保持空间拓扑和局部性的同时进行降维。许多研究人员引入了用于点云处理的空间填充曲线。例如HilbertNet使用希尔伯特曲线将 3D 结构折叠到 2D 空间中，以减少计算量和 GPU 占用。对于 3D 对象检测，一些方法也采用窗口扫描曲线对体素特征进行分组以进行并行计算。本文采用希尔伯特曲线是因为它具有保局部性的有利特性。

点云分组

LiDAR 点云稀疏且分布不均匀，密度各异。因此，现有方法对点或体素进行分组以促进并行计算并降低复杂度。然而，分组只是计算复杂性的折衷方案，限制了信息的流动和有效的感受野。为了解决这个问题，本论文将整个体素建模为一个序列，并允许每个体素了解全局上下文信息。

2 模块介绍

在这里插入图片描述

Voxel Mamba 的概述如图所示。

首先，Voxel Mamba 通过体素特征编码策略将点云转换为稀疏体素。
然后，使用希尔伯特输入层将整个场景的体素序列化为单个序列（与之前执行大量窗口分区和体素分组的基于 Transformer 的方法不同）。
随后，提出了一种作用于体素序列的双尺度 SSM 块，它允许在全局上下文中处理体素。
为了扩大有效感受野，DSB在前向路径中采用更细粒度的体素序列感知；
在后向路径中对体素序列进行下采样。后向路径从低分辨率 BEV 表示中提取特征，并在更深的块中增加下采样因子。
最后，为了增强序列中的空间接近度，Voxel Mamba 采用隐式窗口分区来保留提取的体素特征中的 3D 位置信息，并将其投影到 BEV 特征图。

2.1 希尔伯特输入层（Hilbert Input Layer）

希尔伯特曲线，可以遍历空间中的所有元素而不重复，并保留空间拓扑。
为了提高序列化中体素的接近度，文中提出希尔伯特输入层来重新排序体素序列。

将体素特征的坐标表示为 $\begin{aligned}\mathcal{C}=\{(x,y,z)\in\mathbb{R}^3|0\leq x,y,z\leq n\}\end{aligned}$ 。
将体素映射到其在希尔伯特曲线内的遍历位置 $h$ 上。即将 $(x, y, z)$ 转换为其具有 $log_{2}n$ 位的二进制格式。例如， $x$ 转换为 $x_mx_{m-1}...x_0)$