【MWORKS专业工具箱系列教程】控制系列工具箱第三期：控制系统连接与化简

news2024/9/24 14:10:52

本工具箱教程以控制系统模型创建、分析与设计流程为主线，通过大量示例介绍MWORKS控制系统工具箱的功能和具体使用。共计10篇文章，上一篇主要介绍了控制系统模型转换。

同元软控：【MWORKS专业工具箱系列教程】控制系列工具箱第二期：控制系统模型转换

本教程代码均可直接复制到Syslab中运行，使用教程中代码前需参照下述方法加载函数库内容：
方法一：在Syslab的命令行窗口先后输入using TyControlSystems、using TyPlot和using TyBase并回车(重启软件或命令行窗口后需重新输入)；
方法二：按照下图中的方法预加载函数库(设置好后每次启动软件默认加载)。

第三期：控制系统连接与化简

本期介绍的控制系统模型操作包括两部分：系统连接、系统变换化简

一、系统连接运算

在实际应用中，整个控制系统由被控对象和控制装置组成，存在多个环节组合而成。每个单一模型都可以用一组微分方程或传递函数来描述。模型间连接主要有串联连接、并联连接、串并联连接和反馈连接等。对系统的不同连接情况，可以进行模型的化简

除上述三种典型连接外，Syslab还提供 append()、connect()、lft() 等函数支持一些相对复杂的连接，具体可以参考帮助文档。

在复杂结构框图化简中，经常需要将某个支路的输入点从一个节点移动到另一个节点上，进而便于系统推导与简化。以下是4种典型节点移动的等效变换：

示例13：化简下图的系统，求系统的传递函数

从内层到外层分析模型的环路

output:

julia> loop1
   3s^2 + 5s + 2
--------------------
3s^3 + 7s^2 + 5s + 1

Delay: 0.0

连续时间传递函数模型


julia> loop2
       3s^2 + 5s + 2
---------------------------
3s^4 + 7s^3 + 8s^2 + 6s + 2

Delay: 0.0

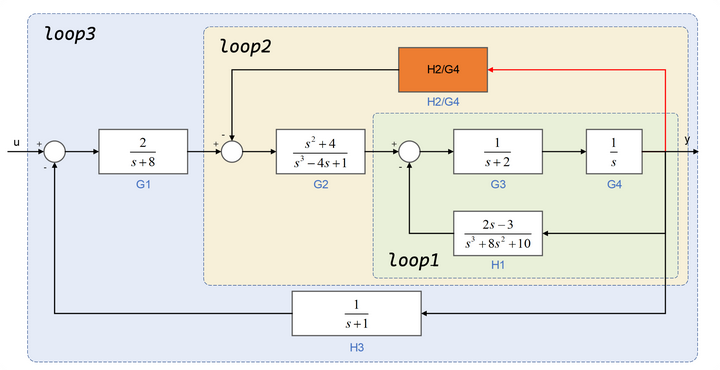
连续时间传递函数模型

示例14：给定一个多回路控制系统的方块图，试对其进行化简

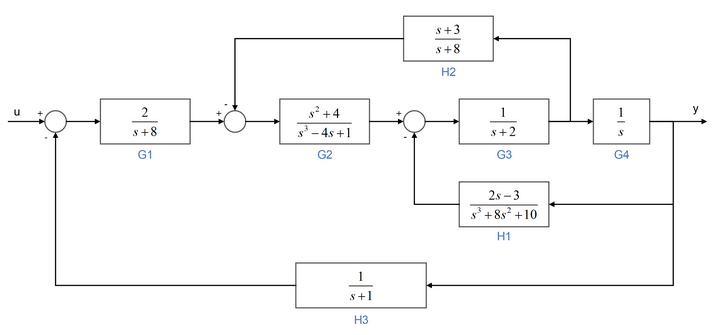
对H2模块进分支点后移，再从内层到外层分析模型的环路

output:

julia> loop1
           s^3 + 8s^2 + 10
-------------------------------------
s^5 + 10s^4 + 16s^3 + 10s^2 + 22s - 3

Delay: 0.0

连续时间传递函数模型


julia> loop2
             s^6 + 16s^5 + 68s^4 + 74s^3 + 336s^2 + 40s + 320
---------------------------------------------------------------------------
s^9 + 18s^8 + 93s^7 + 78s^6 - 236s^5 - 229s^4 - 168s^3 - 550s^2 + 389s - 24

Delay: 0.0

连续时间传递函数模型


julia> loop3
                      2s^7 + 34s^6 + 168s^5 + 284s^4 + 820s^3 + 752s^2 + 720s + 640
---------------------------------------------------------------------------------------------------------
s^11 + 27s^10 + 263s^9 + 1059s^8 + 1210s^7 - 1727s^6 - 4085s^5 - 3758s^4 - 5757s^3 - 251s^2 + 2976s + 448

Delay: 0.0

连续时间传递函数模型

二、线性系统的模型降阶

示例15：考虑以下的系统模型

$G\left( s \right) = \frac{{5{s^3} + 50{s^2} + 155s + 150}}{{{s^4} + 11{s^3} + 41{s^2} + 61s + 30}}$

如果不对其进行任何变换，无法发现该模型有哪些特点

output:

                       (1.0s + 5.0)(1.0s + 3.000000000000009)(1.0s + 1.999999999999996)
5.0----------------------------------------------------------------------------------------------------------- 
   (1.0s + 4.999999999999996)(1.0s + 3.0000000000000084)(1.0s + 1.9999999999999982)(1.0s + 1.0000000000000009) 

Delay: 0.0

连续时间传递函数模型

从零极点模型发现，系统在𝑠=−2、−3、−5处有近似相同的零极点。在数学上就可以直接进行对消(由于精度显示的影响会出现没有直接显示整数的现象，结果中4.999999999999996可当作5.0，其余同理)。

output:

          5.0
-------------------------
1.0s + 1.0000000000000009

Delay: 0.0

连续时间传递函数模型

示例16：考虑以下5阶双输入双输出系统的最小实现

output:

A =
 -1.2278481012658222   -0.19130639750752176   2.7601986869278203
  0.37367324372963995  -1.627513494744153     0.8611642129490126
  0.19052992136656932  -0.21798219140272287  -1.144638403990033
B =
 -8.888194417315589  -7.200562565926553
  0.0                -3.186204440110084
  0.0                 0.0
C =
 -0.675052740555615    0.2701519974158175    0.4344110957473547
 -0.5625439504630119  -0.29796176185568113  -0.08835479913505484
D =
 0.0  0.0
 0.0  0.0

连续时间状态空间模型

原系统与最小实现系统的阶跃响应对比

在模型化简中，均衡实现是状态方程的一种非常实用的表示形式，该模型可以将各个状态变量在整个控制系统中的重要程度明确表示出来。Syslab控制工具箱提供 balreal() 函数可以将已知模型进行均衡实现。

示例17：考虑将以下模型进行简化处理

$G\left( s \right) = \frac{{{s^3} + 11{s^2} + 36s + 26}}{{{s^4} + 14.6{s^3} + 74.96{s^2} + 153.7s + 99.65}}$

① 将上述模型先进行一个均衡状态空间实现

output:

julia> Gb
A =
 -3.601435772897594     0.8212109733891786   -0.6163395682048404    0.058314952589902255
 -0.8212109733891763   -0.5929711329634693    1.0273084167890452   -0.09033395280227531
 -0.6163395682048548   -1.0273084167890418   -5.913814939296773     1.127164702405639
 -0.05831495258988176  -0.09033395280222549  -1.1271647024053315   -4.4917781548421285
B = 
 -1.001984036600179
 -0.106412279753052
 -0.08612411663246879
 -0.008111706668116852
C =
 -1.0019840366001789  0.10641227975305181  -0.08612411663246491  0.008111706668119023
D =
 0.0

连续时间状态空间模型


julia> g
4-element Vector{Float64}:
 0.13938496656762903
 0.009548165713944968
 0.0006271217092401152
 7.3244695977053e-6

通过 Gramian 矩阵的对角线向量 g，判定均衡实现的后 2 个状态对系统影响较小

② 通过 modred() 函数从均衡实现中消除对系统影响较小的状态

output:

julia> Gdel
A =
 -3.601435772897594    0.8212109733891786
 -0.8212109733891763  -0.5929711329634693
B = 
 -1.001984036600179
 -0.106412279753052
C =
 -1.0019840366001789  0.10641227975305181
D =
 0.0

连续时间状态空间模型

原始系统与降阶系统的频率特性对比

output:

系统连接与化简相关主要Syslab函数如下

函数及调用方式	说明
sys = feedback(sys1, sys2)	返回模型对象 sys1、sys2 的负反馈互连的模型对象sys
sys = parallel(sys1, sys2)	两个模型的并联连接
sys = append(sys1, sys2, ..., sysN)	通过增加模型的输入和输出对模型进行分组
sysc = connect(blksys, connections, inputs, outputs)	动态系统的相互连接
sys = lft(sys1, sys2, nu, ny)	两个模型的广义反馈互连(Redheffer星积)
sys = series(sys1, sys2)	两个模型的串联连接
sysb, g = balreal(sys) sysb, g, T = balreal(sys)	基于gramian的状态空间实现的输入/输出平衡
sysr = minreal(sys)	最小实现或极点、零点抵消
rsys = modred(sys, elim, method = value)	从状态空间模型中消除状态
msys = sminreal(sys)	结构极点/零点对消