【排序算法】插入排序_直接插入排序、希尔排序

文章目录

直接插入排序
- 直接插入排序的基本思想
- 直接插入排序的过程
- 插入排序算法的C代码
- 举例分析
- 插入排序的复杂度分析
- 插入排序的优点
希尔排序
- 希尔排序（Shell Sort）详解
- 希尔排序的步骤：
- 希尔排序的过程示例：
- 希尔排序的C语言实现
- 举例分析：
- 希尔排序的复杂度分析：
- 希尔排序的优点和缺点

从本篇文章开始，博主将持续更新排序算法的内容，排序算法如下：

直接插入排序

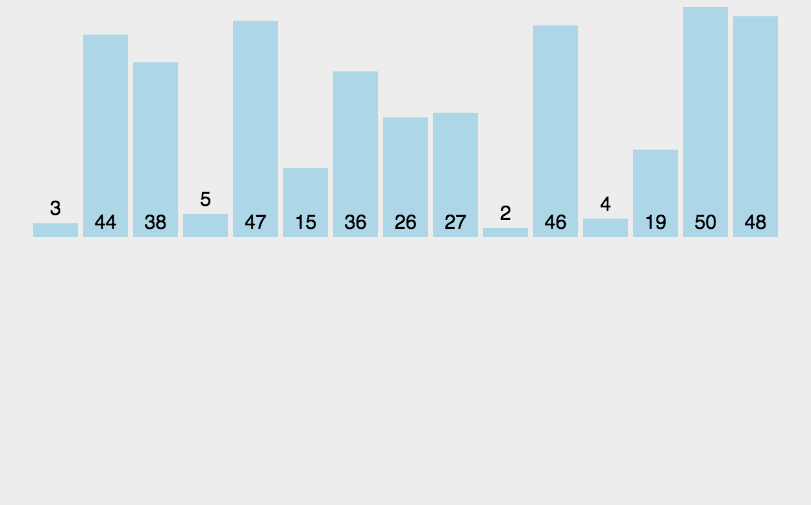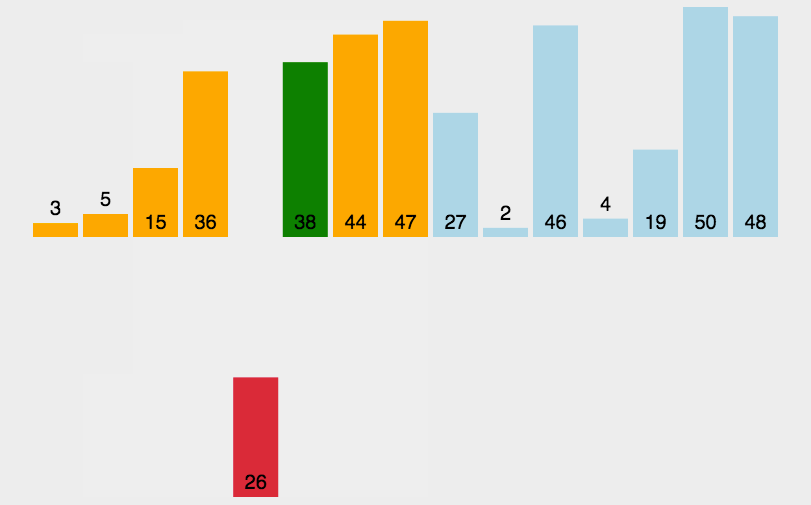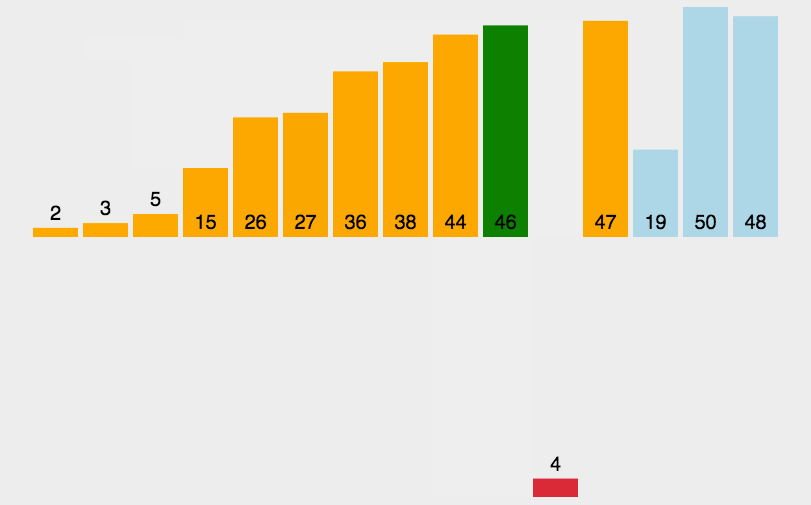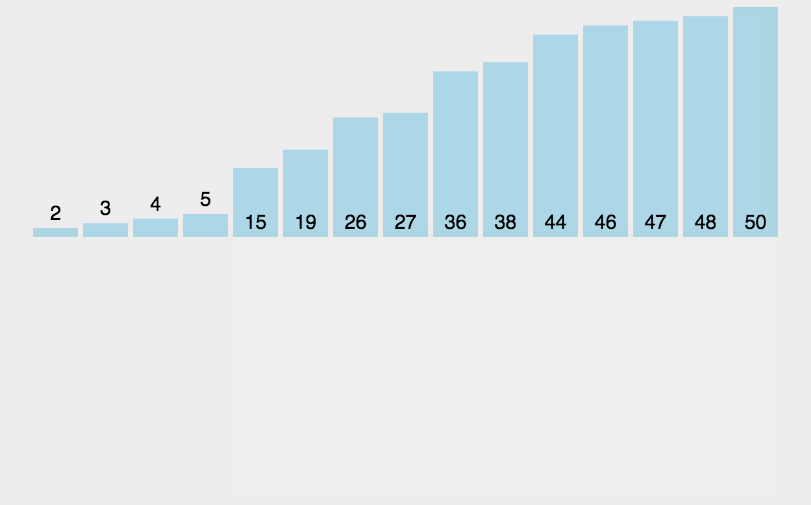
直接插入排序（Simple Insertion Sort）是一种简单的排序算法，基于插入的思想进行排序。它的工作原理类似于我们整理扑克牌的过程：一开始我们手里没有任何牌，每次从桌上取一张牌，将其插入到手中已排好序的牌中，直到手中所有的牌都排好序。

直接插入排序的基本思想

将待排序的数组分为两部分：已排序部分 和 未排序部分。
初始时，已排序部分只有一个元素（通常是数组的第一个元素），未排序部分包含数组中剩下的元素。
每次从未排序部分取出一个元素，插入到已排序部分的合适位置，使已排序部分仍然是有序的。
重复这一过程，直到未排序部分为空。

直接插入排序的过程

从数组的第二个元素开始，假设第一个元素已经排好序。
取当前元素，与已排好序的部分从后向前比较，如果当前元素比前一个元素小，则将前一个元素后移，直到找到适当的位置，将当前元素插入其中。
重复步骤 2，直到所有元素都插入已排序部分，整个数组排序完成。

伪代码：

初始化已排序部分，设第一个元素为已排序部分。
对于第 i 个元素，查找其在前 i-1 个元素中的正确位置。
将元素插入该位置，并将其余元素后移。

插入排序算法的C代码

void InsertSort(int* a, int n) //接收一个数组a和数组的大小n
{
    for (int i = 0; i < n - 1; i++)  // 外层循环，从第1个元素开始，逐个插入到已排序部分
    {
        int end = i;  // 已排序部分的最后一个元素的索引为i
        int tmp = a[end + 1];  // tmp保存当前要插入的元素（未排序部分的第一个元素）

        // 内层循环，用于在已排序部分找到插入tmp的位置
        while (end >= 0)
        {
            if (tmp < a[end])  // 如果当前已排序的元素比tmp大
            {
                a[end + 1] = a[end];  // 把a[end]向后移动一位，为tmp腾出位置
            }
            else
            {
                break;  // 如果找到比tmp小或相等的元素，则退出循环
            }
            --end;  // 继续往前检查前一个元素
        }

        // 当内层循环结束时，end的位置已经是比tmp小的元素，所以tmp应该插入到end+1的位置
        a[end + 1] = tmp;  // 将tmp插入到正确的位置
    }
}

for (int i = 0; i < n - 1; i++) 中的 i < n - 1 是因为插入排序的外层循环控制未排序部分的起始位置。具体原因如下：

在每一次外层循环中，插入排序都会将当前元素（即 a[i + 1]）插入到前面已经排好序的部分。
当 i 达到 n - 1 时，i + 1 就等于 n，这个位置已经超出了数组范围，且所有元素已经排序完毕，所以不需要继续循环。

因此，循环运行到 i < n - 1 就足够保证所有元素都被正确插入排序。

举例分析

我们用一个具体的例子来详细讲解插入排序的过程。假设数组为：

初始数组： [5, 2, 9, 1, 5, 6]

第一步（i = 0）

已排序部分: [5]
未排序部分: [2, 9, 1, 5, 6]
tmp = 2（即当前要插入的元素）

我们比较tmp和已排序部分的元素：

2 < 5，因此将5向后移动，数组变为[5, 5, 9, 1, 5, 6]
tmp插入到位置0，数组变为[2, 5, 9, 1, 5, 6]

第二步（i = 1）

已排序部分: [2, 5]
未排序部分: [9, 1, 5, 6]
tmp = 9

比较tmp与已排序部分：

9 > 5，直接插入，数组保持不变: [2, 5, 9, 1, 5, 6]

第三步（i = 2）

已排序部分: [2, 5, 9]
未排序部分: [1, 5, 6]
tmp = 1

比较tmp与已排序部分：

1 < 9，将9向后移动，得到[2, 5, 9, 9, 5, 6]
1 < 5，将5向后移动，得到[2, 5, 5, 9, 5, 6]
1 < 2，将2向后移动，得到[2, 2, 5, 9, 5, 6]
将tmp插入到位置0，得到[1, 2, 5, 9, 5, 6]

第四步（i = 3）

已排序部分: [1, 2, 5, 9]
未排序部分: [5, 6]
tmp = 5

比较tmp与已排序部分：

5 < 9，将9向后移动，得到[1, 2, 5, 9, 9, 6]
5 == 5，插入tmp到位置3，得到[1, 2, 5, 5, 9, 6]

第五步（i = 4）

已排序部分: [1, 2, 5, 5, 9]
未排序部分: [6]
tmp = 6

比较tmp与已排序部分：

6 < 9，将9向后移动，得到[1, 2, 5, 5, 9, 9]
6 > 5，插入tmp到位置5，得到[1, 2, 5, 5, 6, 9]

最终结果

[1, 2, 5, 5, 6, 9]

插入排序通过不断将元素插入到已排序部分的合适位置，逐步形成有序数组。

插入排序的复杂度分析

● 时间复杂度：
○ 最好情况：O(n)，当数组已经有序时，只需对每个元素进行一次比较。
○ 最坏情况：O(n²)，当数组是反序的，插入每个元素时都要遍历已排序部分的所有元素。
○ 平均情况：O(n²)，通常情况下，每个元素需要和已排序部分的 n/2 个元素进行比较。

● 空间复杂度：O(1)，只需要一个额外的变量 key 来存储待插入的元素，因此插入排序的空间复杂度是常数级的。

插入排序的优点

● 简单易实现：代码实现较为简单，适合少量数据的排序。
● 稳定性：插入排序是一个稳定的排序算法，意味着如果两个元素相等，它们的相对顺序不会在排序过程中改变。
● 适用场景：在数据量较小或者大部分数据已经有序时，插入排序的表现非常好。也适用于顺序存储和链式存储的线性表。

希尔排序

希尔排序（Shell Sort）详解

希尔排序是插入排序的改进版本，它通过逐步缩小步长进行排序，最终达到整体有序。希尔排序又称为缩小增量排序，由计算机科学家 Donald Shell 于 1959 年提出。

希尔排序的基本思想：

步长（Gap）：希尔排序的核心思想是将待排序的数组按一定的步长（增量）分成多个子序列，分别对每个子序列进行插入排序。步长从较大逐渐减小，直至最终为 1。
分组排序：开始时，按较大的步长将数组分为若干个子数组，然后对这些子数组分别进行插入排序。随着步长的减小，子数组变得越来越大，直到步长为 1，整个数组被排序为一个有序序列。
插入排序：在每次分组后，对每个子数组应用插入排序。与直接插入排序不同的是，这些子数组并不是相邻的，而是由指定步长决定的。

希尔排序的步骤：

初始步长：选择一个步长 gap，通常取数组长度的一半。
分组排序：将数组按照 gap 分组，分别对每组元素进行插入排序。
缩小步长：逐步缩小步长，继续对缩小后的分组进行插入排序。
最终步长为 1：当步长为 1 时，整个数组进行一次标准的插入排序，完成最终的排序。

希尔排序的过程示例：

假设我们对数组 [13, 7, 9, 2, 5, 1, 6, 12, 11] 进行希尔排序，按以下步骤进行：

选择初始步长 gap = 4。
- 我们将数组分为 4 组：[13, 5]、[7, 1]、[9, 6]、[2, 12]、[11]。
- 分别对每组进行插入排序。
- 排序后，数组为 [5, 1, 6, 2, 13, 7, 9, 12, 11]。
缩小步长 gap = 2。
- 我们将数组分为 2 组：[5, 6, 13, 9]、[1, 2, 7, 12, 11]。
- 分别对每组进行插入排序。
- 排序后，数组为 [5, 1, 6, 2, 9, 7, 13, 12, 11]。
最终步长 gap = 1。
- 此时相当于对整个数组进行一次插入排序。
- 最终结果为 [1, 2, 5, 6, 7, 9, 11, 12, 13]。

希尔排序的C语言实现

void ShellSort(int* a, int n)
{
    int gap = n;  // 初始化gap为数组长度n，表示最初的间隔大小
    while (gap > 1)  // 当gap大于1时，不断进行循环
    {
        gap = gap / 2;  // 每次将gap减半，逐渐缩小间隔

        // 针对每个分组进行插入排序
        for (int j = 0; j < gap; j++) {
            // 在这里，数组会被分为多个以 gap 为间隔的子序列，下面对每个子序列进行插入排序
            for (int i = j; i < n - gap; i += gap) {
                int end = i;  // 当前要插入的元素的前一个元素的位置
                int tmp = a[end + gap];  // 保存待插入的元素

                // 插入排序过程：将tmp插入到其正确的位置
                while (end >= 0) {
                    if (tmp < a[end]) {
                        a[end + gap] = a[end];  // 如果tmp小于当前元素，将当前元素向后移动gap个位置
                        end -= gap;  // 将end向前移动gap个位置，继续比较
                    }
                    else {
                        break;  // 找到位置，跳出循环
                    }
                }
                a[end + gap] = tmp;  // 将tmp插入到正确的位置
            }
        }
    }
}

i < n - gap 的条件是为了确保 i + gap 不会超出数组的范围。因为在 Shell 排序中，我们会用 a[i + gap] 来与前面的元素进行比较和移动。

举个例子：

假设数组长度 n = 8，当前 gap = 4。

初始 j = 0，i = 0。
当 i < n - gap = 8 - 4 = 4 成立时，i 的值可以是 0, 4。

如果 i 达到 4，那么 i + gap = 4 + 4 = 8，这正好是数组的最后一位（超出范围）。

所以，限制条件 i < n - gap 可以确保 i + gap 仍然在数组范围内，避免越界访问。

举例分析：

我们用一个大小为8的数组：{8, 5, 7, 3, 2, 6, 4, 1}，详细讲解希尔排序的过程。

初始状态

数组：{8, 5, 7, 3, 2, 6, 4, 1}
长度 n = 8

第一步：确定初始 gap

gap = n / 2 = 4（第一次间隔为4）

以 gap = 4 进行分组和排序

此时数组被分为4个子序列，分别是：

序列1: 8, 2 （索引0和4）
序列2: 5, 6 （索引1和5）
序列3: 7, 4 （索引2和6）
序列4: 3, 1 （索引3和7）

现在我们对每个子序列进行插入排序。

对第一个子序列 {8, 2} 插入排序

j = 0（第一个分组的起始索引）
i = j = 0
end = 0，tmp = a[end + gap] = a[4] = 2
比较 tmp (2) 和 a[end] (8)：
- 2 < 8，因此 a[end + gap] = a[0 + 4] = a[4] 被替换为 8
- 数组变为 {8, 5, 7, 3, 8, 6, 4, 1}
- end 继续向前移动4个位置变成 -4，停止移动。
将 tmp (2) 放到 end + gap = 0，数组变为 {2, 5, 7, 3, 8, 6, 4, 1}

对第二个子序列 {5, 6}

j = 1，i = 1
end = 1，tmp = a[end + gap] = a[5] = 6
比较 tmp (6) 和 a[end] (5)：6 > 5，无需移动。
数组保持不变：{2, 5, 7, 3, 8, 6, 4, 1}

对第三个子序列 {7, 4}

j = 2，i = 2
end = 2，tmp = a[end + gap] = a[6] = 4
比较 tmp (4) 和 a[end] (7)：4 < 7
- a[end + gap] = a[6] = 7，数组变为 {2, 5, 7, 3, 8, 6, 7, 1}
- end 继续向前移动4个位置，变成 -2，停止移动。
将 tmp (4) 放到 end + gap = 2，数组变为 {2, 5, 4, 3, 8, 6, 7, 1}

对第四个子序列 {3, 1}

j = 3，i = 3
end = 3，tmp = a[end + gap] = a[7] = 1
比较 tmp (1) 和 a[end] (3)：1 < 3
- a[end + gap] = a[7] = 3，数组变为 {2, 5, 4, 3, 8, 6, 7, 3}
- end 继续向前移动4个位置，变成 -1，停止移动。
将 tmp (1) 放到 end + gap = 3，数组变为 {2, 5, 4, 1, 8, 6, 7, 3}

第二步：更新 gap

gap = gap / 2 = 2

以 gap = 2 进行分组和排序

此时数组被分为两个子序列，每间隔2个元素组成一组：

第一组：**{2, 4, 8, 7}**

插入排序过程：
- i = 0, end = 0, tmp = 4，无需调整。
- i = 2, end = 2, tmp = 8，无需调整。
- i = 4, end = 4, tmp = 7，无需调整。

数组保持 {2, 5, 4, 1, 8, 6, 7, 3}

第二组：{5, 1, 6, 3}

插入排序过程：
- i = 1, end = 1, tmp = 1
  - 1 < 5，将 5 向后移动，数组变为 {2, 5, 4, 5, 8, 6, 7, 3}
  - 插入 1，得到 {2, 1, 4, 5, 8, 6, 7, 3}
- i = 3, end = 3, tmp = 6，无需调整。
- i = 5, end = 5, tmp = 3
  - 3 < 6，将 6 向后移动，数组变为 {2, 1, 4, 5, 8, 6, 7, 6}
  - 插入 3，得到 {2, 1, 4, 3, 8, 5, 7, 6}

第三步：更新 gap

gap = gap / 2 = 1，此时进行标准插入排序。

以 gap = 1 进行排序

数组：{2, 1, 4, 3, 8, 5, 7, 6}

对每个元素进行插入排序：
- i = 1, tmp = 1，插入后 {1, 2, 4, 3, 8, 5, 7, 6}
- i = 2, tmp = 4，无需调整
- i = 3, tmp = 3，插入后 {1, 2, 3, 4, 8, 5, 7, 6}
- i = 4, tmp = 8，无需调整
- i = 5, tmp = 5，插入后 {1, 2, 3, 4, 5, 8, 7, 6}
- i = 6, tmp = 7，插入后 {1, 2, 3, 4, 5, 7, 8, 6}
- i = 7, tmp = 6，插入后 {1, 2, 3, 4, 5, 6, 7, 8}

最终排序结果

{1, 2, 3, 4, 5, 6, 7, 8}

希尔排序的复杂度分析：

时间复杂度：
- 希尔排序的时间复杂度依赖于选择的步长序列。一般使用的步长序列是 gap = n/2, n/4, ..., 1。
- 最坏情况时间复杂度：O(n²)（当步长序列选择不当时，可能退化为插入排序）。
- 最好情况时间复杂度：O(n)（当数组已部分有序时）。
- 平均时间复杂度：O(n^1.5)，在实际应用中往往比 O(n²) 的排序算法快。
空间复杂度：
- 希尔排序是一种原地排序算法，只需常数级别的额外空间，即 O(1)。
稳定性：
- 希尔排序是不稳定的，因为相隔较远的元素可能会交换位置，破坏了相同元素之间的相对顺序。

希尔排序的优点和缺点

优点：
- 相比于直接插入排序，希尔排序能够显著减少元素的移动次数，尤其是在数据量较大时表现更为出色。
- 希尔排序在最坏情况下比 O(n²) 的算法快很多，尤其是接近有序的数据集。
缺点：
- 希尔排序是不稳定的排序算法。
- 其性能依赖于步长的选择，不同的步长序列会有不同的表现，且最优的步长序列是一个开放性问题。