文章目录
- 1 引言
- 2 经典报童问题
- 3 带广告的报童问题
- 3.1 论文解读
- 3.2 样本均值近似方法
- 4 多产品报童问题
- 4.1 论文解读
- 4.2 算法模型
- 4.3 简单实例求解
- 4.4 复杂实例求解
- 5 总结
- 6 相关阅读
1 引言
中秋已过,国庆未至,趁着这个空窗期,学点新知识,充实一下自己,多是一件美事!
这次要学习的内容,可以看做是一文了解经典报童模型的扩展问题的延续。在那篇文章里,经典报童模型的扩展问题被分成了5种类型:扩展目标函数、增加约束条件、增加优化变量、扩展模型参数和扩展问题场景。至于每种扩展问题应该如何求解,并没有再过多介绍。
从我个人的认知来看,只了解综述,不清楚如何求解的话,会觉得理解的深度有点浅;另一方面,扩展问题类型太多,又不太可能把所有问题类型都求解一遍,所以本文将选择两类比较常见的扩展问题来求解:带广告的报童问题(single-period problem with advertising,SPPWA)和多产品报童问题(multi-product Newsboy problem, MPNP),其中前者属于扩展模型参数的类型,后者属于增加优化变量的类型。
正文见下。
2 经典报童问题
在研究扩展问题前,再回顾一下经典报童模型(SPP)。
经典报童模型可以描述为:报童每天从供应商处采购一定数量的报纸用于当天的销售。已知每份报纸的成本价 c c c,销售价 p p p,需求量 d d d是个不确定参数,通过历史的数据可知其概率分布函数,如果当天卖不完,会按回收价 s s s将未卖完的报纸卖给回收站。
该模型的核心诉求是:确定报童的最佳订购量
x
x
x,使得报童的净收入
θ
(
x
)
\theta(x)
θ(x)最大化。其中
θ
(
x
)
\theta(x)
θ(x)的表达式为
θ
(
x
)
=
p
⋅
E
[
min
(
x
,
d
)
]
+
s
⋅
E
[
max
(
x
−
d
,
0
)
]
−
c
x
\theta(x)=p·E[\min(x,d)]+s·E[\max(x-d,0)]-cx
θ(x)=p⋅E[min(x,d)]+s⋅E[max(x−d,0)]−cx
其中,第一项是售卖报纸的收益,第二项是回收报纸的收益,第三项是购买报纸的成本。
SPP的求解算法,可以参考:随机规划:求解报童问题期望值模型的算法方案。
3 带广告的报童问题
SPPWA相比SPP的区别是:报童可以给予报纸一定的广告投入,投入广告后,会改变(大概率是增加)原有的需求量,为了最大化收益,需要在决策订购量的同时,决策投入的广告预算。
3.1 论文解读
在研究SPPWA的论文中,本文选择如下这篇进行介绍:Linking advertising and quantity decisions in the single-period inventory model。这篇文章发表于2003年,虽然年代有些久远,但是初步阅读下来发现,这篇文章对于SPPWA的求解还是很有启发性的。
其核心内容是:针对SPPWA,当广告和需求的关系是如下表中的三种关系之一时,分别设定目标函数为最大化预期利润和最大化达到目标利润的概率,均可推导出解析最优解。
| 广告和需求的关系 | 需求分布函数 |
|---|---|
| CVC:需求的均值增加,方差不变 | 均匀分布、正态分布 |
| CCVC:需求的均值和方差同比例增加 | 均匀分布、正态分布、指数分布 |
| ICVC:需求的均值和方差都增加,但是方差增长的更快 | 均匀分布、正态分布 |
需要说明的是,由于调研的精力有限,该文章不一定是求解SPPWA的最佳方案,只是看到这篇文章后,感觉已经解答了我心中所惑,所以就选择了这篇文章。
本节接下来的重点,不是还原论文推导的原过程,而是在原文理解的基础上,尝试通过其他更简单和直观的方法,去求解SPPWA,同时和解析解的结果做对比,从而加深对此类问题的理解。
3.2 样本均值近似方法
要求解SPPWA,首先需要明确需求量
d
d
d和广告
B
B
B间的关系。这里采用论文中使用的表达式:
d
=
d
0
(
1
+
w
B
α
)
d = d_0(1+wB^{\alpha})
d=d0(1+wBα)
其中,
d
0
d_0
d0是没广告时的需求量,
w
w
w和
α
\alpha
α是经验参数。特别地,(1)如果
w
w
w为0,表示需求和广告之间没有关系;(2)需要限制
0
≤
α
≤
1
0≤\alpha≤1
0≤α≤1,此时,随着广告预算
B
B
B的增加,需求量
d
d
d的增加效应是边际递减的,这才符合我们的一般认知。下图是三个具体的实例。
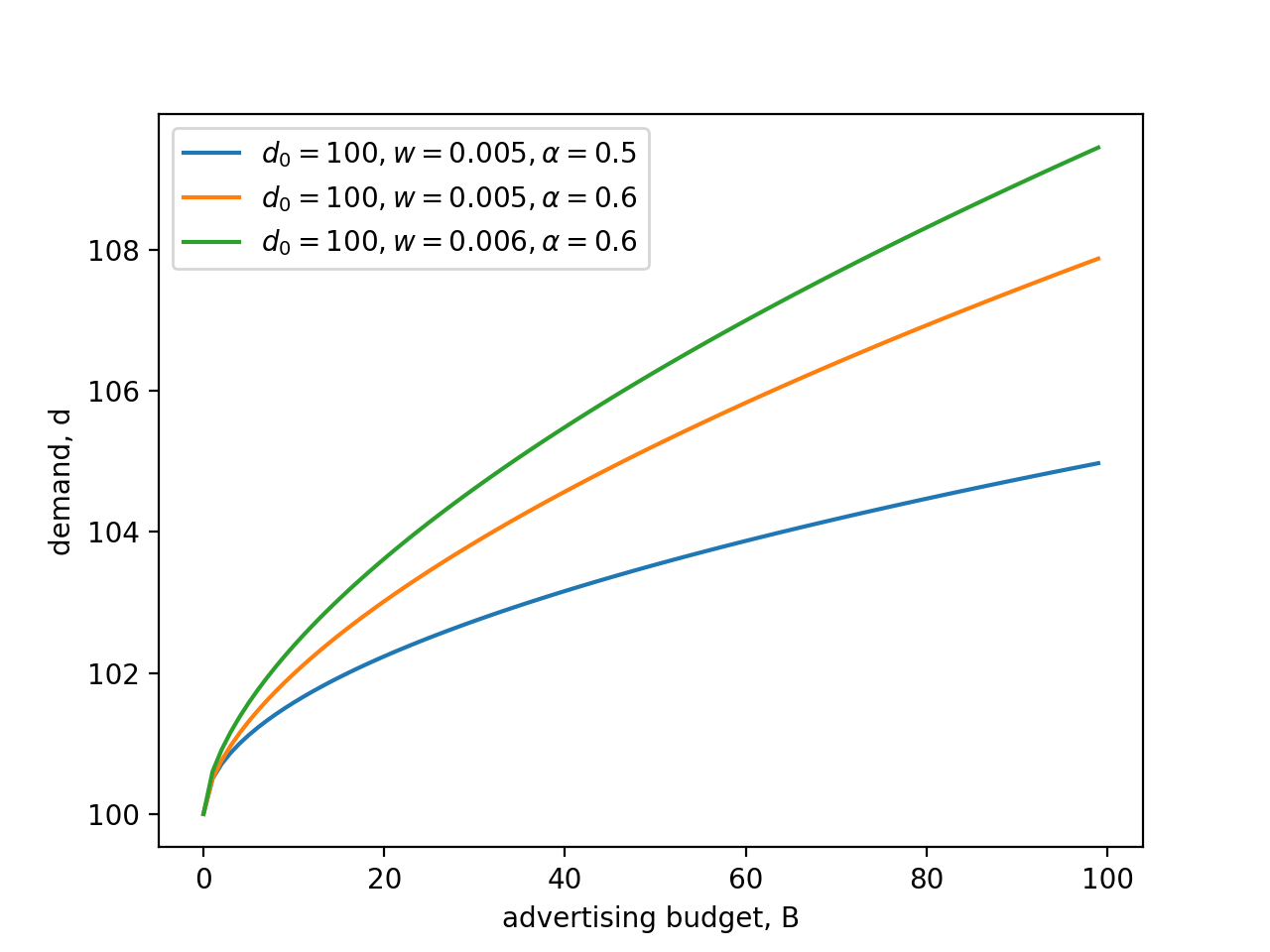
需要额外说明的是,这个表达式不具备一般通用性。在实际业务场景中,需求量
d
d
d和广告
B
B
B间的关系大概率需要单独开发一个因果推断模型来刻画,例如:
Δ
d
d
=
α
⋅
Δ
B
B
+
b
\frac{\Delta d}{d} = \alpha · \frac{\Delta B}{B} + b
dΔd=α⋅BΔB+b
即两者的变化率是线性的。在此基础上,基于历史的广告和需求量数据,使用双重机器学习等因果推断算法得到
α
\alpha
α值。
如果换成这种表达式,论文中的解析表达式将会不再适用。为了让求解算法能适应更多场景,本节将以样本均值近似方法为基础,然后再将把广告预算这个额外待优化的变量考虑进来。此处选用样本均值近似方法的另一个原因是:相比SPP,SPPWA在本质上只是多了广告预算这一个优化变量,并不会大幅增加求解时间。
接下来,将以ICVC为实例,进行求解。此时需求量
d
d
d和广告
B
B
B间的关系为
μ
=
μ
0
(
1
+
w
B
α
)
,
σ
=
σ
0
(
1
+
w
B
α
)
(
1
+
g
B
γ
)
\mu = \mu_0(1+wB^{\alpha}), \sigma = \sigma_0(1+wB^{\alpha})(1+gB^{\gamma})
μ=μ0(1+wBα),σ=σ0(1+wBα)(1+gBγ)
仿真参数和论文保持一致:
P
=
100
P = 100
P=100,
C
=
60
C=60
C=60,
V
=
40
V=40
V=40,
S
=
10
S=10
S=10,这些参数的含义已经在代码中标出,需要注意的是,他们和第2节中的参数含义并不完全一致,这里主要是为了和论文保持一致,所以没有刻意对齐上文;
d
d
d满足正态分布,且
μ
=
1000
\mu=1000
μ=1000,
σ
=
200
\sigma=200
σ=200,广告相关参数为:
α
=
0.5
\alpha=0.5
α=0.5,
w
=
0.005
w=0.005
w=0.005,
g
=
0.02
g=0.02
g=0.02,
γ
=
0.4
\gamma=0.4
γ=0.4。
以下为求解的Python代码。相比经典报童问题的求解代码,首先是多了一层针对广告预算 B B B的for循环;然后是目标函数里多了两项: − s ∗ max ( cur d − cur x , 0 ) - s * \max(\text{cur}_d -\text{cur}_x, 0) −s∗max(curd−curx,0)和 − B -B −B,其中第一项表示减去缺货损失值,第二项表示减去广告预算值。
import numpy as np
if __name__ == '__main__':
# 报童模型参数
c = 60 # 成本价
s = 10 # 缺货价
p = 100 # 单位卖价
v = 40 # 回收价
# 广告模型参数
w = 0.005
alpha = 0.5
g = 0.02
gamma = 0.4
# 最优解
best_f = 0 # 最大收益
best_x = 0 # 最佳购买量
best_B = 0 # 最佳广告预算
np.random.seed(42)
# 遍历所有决策变量x
for cur_x in range(500, 2000, 100):
# 遍历所有广告预算
for B in range(1000, 20000, 100):
cur_f = 0
# 需求分布,ICVC
mu0 = 1000
mu = mu0 + mu0 * w * B ** alpha
sigma0 = 200
sigma = sigma0 * (1 + w * B ** alpha) * (1 + g * B ** gamma)
d = np.random.normal(mu, sigma, 10000)
# 统计收益
for cur_d_index in range(len(d)):
cur_d = d[cur_d_index]
# 计算当前决策变量和当前需求值时的值
cur_f += p * min(cur_x, cur_d) + v * max(cur_x - cur_d, 0) - c * cur_x - s * max(cur_d - cur_x, 0) - B
# 更新最优解
if cur_f / len(d) > best_f:
best_f = cur_f / len(d)
best_x = cur_x
best_B = B
print('best_x: {}, best_B: {}, best_f: {}.'.format(best_x, best_B,best_f))
运行代码后,可以得到最优解如下。
best_x: 1500, best_B: 3700, best_f: 39198.29929996124.
从论文可知,解析解为
x
=
1613
,
B
=
3602
,
f
=
38940
x=1613, B = 3602, f = 38940
x=1613,B=3602,f=38940
对比两组解发现,两者的差异并不大,主要差异应该是来源于
d
d
d和
B
B
B的离散化处理,整体上是符合预期的。
4 多产品报童问题
MPNP相比SPP的区别是:报童可以采购的报纸类型有多种,每一种类型的报纸成本、销售价、需求量和回收价均不同;同时报童的总预算上限有约束。为了最大化收益,就需要同时决策每一种报纸的订购量。
4.1 论文解读
在研究MPNP的论文中,本文选择如下这篇进行介绍::Exact, approximate, and generic iterative models for the multi-product Newsboy problem with budget constraint。
这篇文章的核心内容是:针对MPNP,提出了一种通用的迭代求解算法,如果需求的分布为均匀分布,可以得到精确解;如果需求的分布为一般化的函数,则随着迭代次数的增加,可以逐步逼近期望的精度水平。
和上一章类似,本章接下来的内容,不是复现原文,而是在对原文理解的基础上,尝试使用其他方法替代文中迭代求解的方法,去求解MPNP。
4.2 算法模型
针对MPNP,目标函数为
min
E
=
∑
τ
=
1
N
[
c
τ
x
τ
+
h
τ
∫
0
x
τ
(
x
τ
−
D
τ
)
f
τ
(
D
τ
)
d
D
τ
+
v
τ
∫
x
τ
∞
(
D
τ
−
x
τ
)
f
τ
(
D
τ
)
d
D
τ
]
\min \ E=\sum_{\tau=1}^N[c_{\tau}x_{\tau}+h_{\tau}\int_0^{x_{\tau}}(x_{\tau}-D_{\tau})f_{\tau}(D_{\tau})dD_{\tau}+v_{\tau}\int_{x_{\tau}}^{\infty}(D_{\tau}-x_{\tau})f_{\tau}(D_{\tau})dD_{\tau}]
min E=τ=1∑N[cτxτ+hτ∫0xτ(xτ−Dτ)fτ(Dτ)dDτ+vτ∫xτ∞(Dτ−xτ)fτ(Dτ)dDτ]
式中,
E
E
E为预期费用,所以目标是最小化;
τ
(
=
1
,
2
,
.
.
.
,
N
)
\tau(=1,2,...,N)
τ(=1,2,...,N)是产品编号,
N
N
N是产品总数量;
c
τ
c_{\tau}
cτ是第
τ
\tau
τ个产品的单价;
x
τ
x_{\tau}
xτ是第
τ
\tau
τ个产品的订购量;
h
τ
h_{\tau}
hτ是第
τ
\tau
τ个产品未卖完情况下的剩余价值(残值);
D
τ
D_{\tau}
Dτ是第
τ
\tau
τ个产品的需求量;
f
τ
(
D
τ
)
f_{\tau}(D_{\tau})
fτ(Dτ)是第
τ
\tau
τ个产品的需求概率密度函数;
v
τ
v_{\tau}
vτ是第
τ
\tau
τ个产品的利润。整体来看,上述公式可以理解为包含三类费用:第一项为购买产品的成本,第二项是多亏的钱,第三项为少赚的钱。
约束条件为
∑
τ
=
1
N
c
τ
x
τ
≤
B
G
\sum_{\tau = 1}^N c_{\tau}x_{\tau}≤B_G
τ=1∑Ncτxτ≤BG
式中,
B
G
B_G
BG指的是预算上限。
求解的过程可以分为三步:
(1) 假设不存在约束条件,MPNP可以直接转化为多个相互独立的SPP,然后分别求解得到 x τ ∗ x_{\tau}^{\ast} xτ∗。
(2) 如果 x τ ∗ x_{\tau}^{\ast} xτ∗满足约束条件,则该解也是MPNP的最优解,直接退出;否则继续执行第三步。
(3) 从 x τ ∗ x_{\tau}^{\ast} xτ∗开始迭代,直至约束条件被满足。
第一步单产品最优解
x
τ
∗
x_{\tau}^{\ast}
xτ∗的求解可以参考之前的文章:随机规划:求解报童问题期望值模型的算法方案。这里已经不再是重点,直接给出最终公式为
F
τ
(
x
τ
∗
)
=
v
τ
−
c
τ
v
τ
+
h
τ
=
θ
τ
F_{\tau}(x_{\tau}^{\ast})=\frac{v_{\tau}-c_{\tau}}{v_{\tau}+h_{\tau}}=\theta_{\tau}
Fτ(xτ∗)=vτ+hτvτ−cτ=θτ
此处,
F
τ
(
x
τ
∗
)
F_{\tau}(x_{\tau}^{\ast})
Fτ(xτ∗)是
x
τ
∗
x_{\tau}^{\ast}
xτ∗的累积分布函数。
第二步验证 x τ ∗ x_{\tau}^{\ast} xτ∗是否满足约束,也无需赘述。
所以重点是,第三步的详细步骤,接下来将详细描述。
对于带约束的优化问题,一种可行的方案是:拉格朗日乘子法。在该场景中,目标函数变为
min
L
=
∑
τ
=
1
N
[
c
τ
x
τ
+
h
τ
∫
0
x
τ
(
x
τ
−
D
τ
)
f
τ
(
D
τ
)
d
D
τ
+
v
τ
∫
x
τ
∞
(
D
τ
−
x
τ
)
f
τ
(
D
τ
)
d
D
τ
]
+
λ
(
∑
τ
=
1
N
c
τ
x
τ
−
B
G
)
\min \ L=\sum_{\tau=1}^N[c_{\tau}x_{\tau}+h_{\tau}\int_0^{x_{\tau}}(x_{\tau}-D_{\tau})f_{\tau}(D_{\tau})dD_{\tau}+v_{\tau}\int_{x_{\tau}}^{\infty}(D_{\tau}-x_{\tau})f_{\tau}(D_{\tau})dD_{\tau}] + \lambda (\sum_{\tau = 1}^N c_{\tau}x_{\tau}-B_G)
min L=τ=1∑N[cτxτ+hτ∫0xτ(xτ−Dτ)fτ(Dτ)dDτ+vτ∫xτ∞(Dτ−xτ)fτ(Dτ)dDτ]+λ(τ=1∑Ncτxτ−BG)
最优解变为
F
τ
(
x
τ
∗
∗
)
=
v
τ
−
c
τ
(
1
+
λ
)
v
τ
+
h
τ
F_{\tau}(x_{\tau}^{\ast \ast})=\frac{v_{\tau}-c_{\tau}(1+\lambda)}{v_{\tau}+h_{\tau}}
Fτ(xτ∗∗)=vτ+hτvτ−cτ(1+λ)
从上式可知,只要得到了
λ
\lambda
λ的值,
x
τ
∗
∗
x_{\tau}^{\ast \ast}
xτ∗∗的值也就得到了。
4.3 简单实例求解
为了更好地展示如何得到 λ \lambda λ的过程,我们先找个具体的实例来感受一下。
最简单的实例应该是: D τ D_{\tau} Dτ的分布为均匀分布。假设最大值为 b τ b_{\tau} bτ,最小值为 a τ a_{\tau} aτ,则 D τ D_{\tau} Dτ的累积分布函数为

把上式代入
F
τ
(
x
τ
∗
∗
)
F_{\tau}(x_{\tau}^{\ast \ast})
Fτ(xτ∗∗),可以得到
x
τ
∗
∗
=
(
b
τ
−
a
τ
)
⋅
v
τ
−
c
τ
(
1
+
λ
)
v
τ
+
h
τ
+
a
τ
x_{\tau}^{\ast\ast}=(b_{\tau}-a_{\tau})·\frac{v_{\tau}-c_{\tau}(1+\lambda)}{v_{\tau}+h_{\tau}}+a_{\tau}
xτ∗∗=(bτ−aτ)⋅vτ+hτvτ−cτ(1+λ)+aτ
由于
x
τ
∗
x_{\tau}^{\ast}
xτ∗不满足预算约束,且
x
τ
∗
∗
x_{\tau}^{\ast\ast}
xτ∗∗为最优解,所以此时的约束变为硬约束
∑
τ
=
1
N
(
c
τ
x
τ
∗
∗
)
−
B
G
=
0
\sum_{\tau=1}^N (c_{\tau}x_{\tau}^{\ast\ast})-B_G=0
τ=1∑N(cτxτ∗∗)−BG=0
将上上式代回上式,便可以解出
λ
\lambda
λ
λ
=
Δ
C
∑
τ
=
1
N
(
b
τ
−
a
τ
)
⋅
[
c
τ
2
/
(
v
τ
+
h
τ
)
]
\lambda=\frac{\Delta C}{\sum_{\tau=1}^N (b_{\tau}-a_{\tau})·[c_{\tau}^2/(v_{\tau}+h_{\tau})]}
λ=∑τ=1N(bτ−aτ)⋅[cτ2/(vτ+hτ)]ΔC
此处
Δ
C
=
∑
τ
=
1
N
(
c
τ
x
τ
∗
)
−
B
G
\Delta C=\sum_{\tau=1}^N (c_{\tau}x_{\tau}^{\ast})-B_G
ΔC=∑τ=1N(cτxτ∗)−BG,可以理解为
x
τ
∗
x_{\tau}^{\ast}
xτ∗情况下约束不满足的程度。
过程挺简单的,再整理一下具体的求解过程,核心就三步:①确定累积分布函数 F τ ( D τ ) F_{\tau}(D_{\tau}) Fτ(Dτ);②使用累计分布函数反解 x τ ∗ ∗ x_{\tau}^{\ast\ast} xτ∗∗的表达式,此时表达式中包含 λ \lambda λ;③将 x τ ∗ ∗ x_{\tau}^{\ast\ast} xτ∗∗的表达式代入硬约束条件,求出 λ \lambda λ值。
4.4 复杂实例求解
如果 D τ D_{\tau} Dτ的分布不是均匀分布,而是更复杂的分布函数,上述的步骤①和②可以继续求解,但③可能无法得到 λ \lambda λ的解析表达式。
到了这一步,论文中使用泰勒展开式,按展开的项数,分别给出近似项和误差项,当误差项的值低于允许的误差最大值后,近似项就可以认为是最优解。
但事实上,步骤③的求解本质上就是个一元的求根问题,鉴于现在的数值优化能力已经足够强大,我们可以直接使用数值的方式高效求出 λ \lambda λ值,不用再去推导复杂的表达式。
接下来,我们看一个
D
τ
D_{\tau}
Dτ的分布为指数分布的实例,此时
F
τ
(
D
τ
)
=
1
−
e
−
μ
τ
D
τ
,
for
D
τ
>
0
F_{\tau}(D_{\tau})=1-e^{-\mu_{\tau}D_{\tau}}, \ \text{for} \ D_{\tau} > 0
Fτ(Dτ)=1−e−μτDτ, for Dτ>0
x
τ
∗
∗
=
−
μ
τ
ln
(
1
−
v
τ
−
c
τ
(
1
+
λ
)
v
τ
+
h
τ
)
x_{\tau}^{\ast\ast}=-\mu_{\tau} \ln(1-\frac{v_{\tau}-c_{\tau}(1+\lambda)}{v_{\tau}+h_{\tau}})
xτ∗∗=−μτln(1−vτ+hτvτ−cτ(1+λ))
其中,
μ
τ
\mu_{\tau}
μτ为第
τ
\tau
τ个产品的指数分布函数的参数。
将上述 x τ ∗ ∗ x_{\tau}^{\ast\ast} xτ∗∗代入硬约束,再调用scipy.optimize.fsolve函数便可求解出 λ \lambda λ。
以下为求解的Python代码。其中,产品数量为6个,预算上限为3500,其他参数如 v τ v_{\tau} vτ、 h τ h_{\tau} hτ、 c τ c_{\tau} cτ和 μ τ \mu_{\tau} μτ也和论文中保持一致。
import math
from scipy.optimize import fsolve
import numpy as np
# 迭代计算模型
def f1(x, c, mu, v, h, b_g):
return (c * (-mu) * np.log(1 - (v - c * (1 + x)) / (v + h))).sum() - b_g
if __name__ == '__main__':
# MPNP参数
item_cnt = 6 # 产品数量
v = np.array([7, 12, 30, 30, 40, 45]) # 卖价
h = np.array([1, 2, 4, 4, 2, 5]) # 滞销价
c = np.array([4, 8, 20, 10, 13, 15]) # 成本价
b_g = 3500 # 预算约束
mu = np.array([200, 225, 112.5, 100, 75, 30]) # 指数分布参数
x0 = [] # SPP的解
delta_C = -b_g
theta = []
for i in range(item_cnt):
theta.append((v[i] - c[i]) / (v[i] + h[i]))
x0.append(- mu[i] * math.log(1 - theta[i]))
delta_C += c[i] * x0[i]
if delta_C <= 0:
# SPP已经是最优解,直接输出
print('SPP satisfies the constraint, best_x: {}'.format(x0))
else:
# SPP不是最优解,需要迭代
theta = np.array(theta)
sol = fsolve(f1, 0, args=(c, mu, v, h, b_g, )) # 使用x0的解为初值,此时lambda0=0
best_x = (-mu) * np.log(1 - (v - c * (1 + sol)) / (v + h)) # 基于最优解重新计算x
print('SPP does not satisfy the constraint, best_x: {}'.format(best_x))
运行代码后,得到最优解如下。该解和论文中的解几乎一致,验证了求解方案的正确性。
SPP does not satisfy the constraint, best_x: [78.44198293 58.20266745 30.08242137 81.75608862 70.92060077 25.29557367]
5 总结
文章正文到此就结束了,本节做个简单的总结:
(1)针对带广告的报童问题,当广告和需求量的关系满足一定的关系时,可以得到解析解;使用样本均值近似方法也可以快速求解。
(2)针对多产品报童问题,采用迭代求解的方法,可以逐步逼近最优解;也可以使用数值求解的方法直接得到最优解。
6 相关阅读
带广告的报童问题:https://www.sciencedirect.com/science/article/abs/pii/S0925527303000082
多产品报童问题:https://www.sciencedirect.com/science/article/abs/pii/S0925527303002901
拉格朗日乘子法:https://mp.weixin.qq.com/s/cljmqvklV4OcBYov22ag3A?token=1853406253&lang=zh_CN
经典报童问题求解方案:https://mp.weixin.qq.com/s/4yzjz2YhkHbVYL8H78qX5w?token=1853406253&lang=zh_CN
经典报童模型扩展综述:https://mp.weixin.qq.com/s?__biz=MzIyMzc3MjIyMw==&mid=2247485123&idx=1&sn=068d9e682d3a27ad8af91f029bb49c53&chksm=e8186d93df6fe485ef4e455e110f6339e0cd67c73d32451e2bd9648480c5a5cf17685c042758&token=1111227419&lang=zh_CN#rd








![re题(38)BUUCTF-[FlareOn6]Overlong](https://i-blog.csdnimg.cn/direct/9b47ac03866f4faab77c654e413bf047.png)




![[Python学习日记-26] Python 中的文件操作](https://i-blog.csdnimg.cn/direct/b0fc572199b44f63b09982394dadf828.png)