晶体与晶体结构Crystal and Crystal Structure
1.晶体主要特征
固态物质可以分为晶态和非晶态两大类,分别称为晶体和非晶体。
晶体和非晶体在微观结构上的区别在于是否具有长程有序。
- 晶体(长程有序)
- 非晶(短程有序)
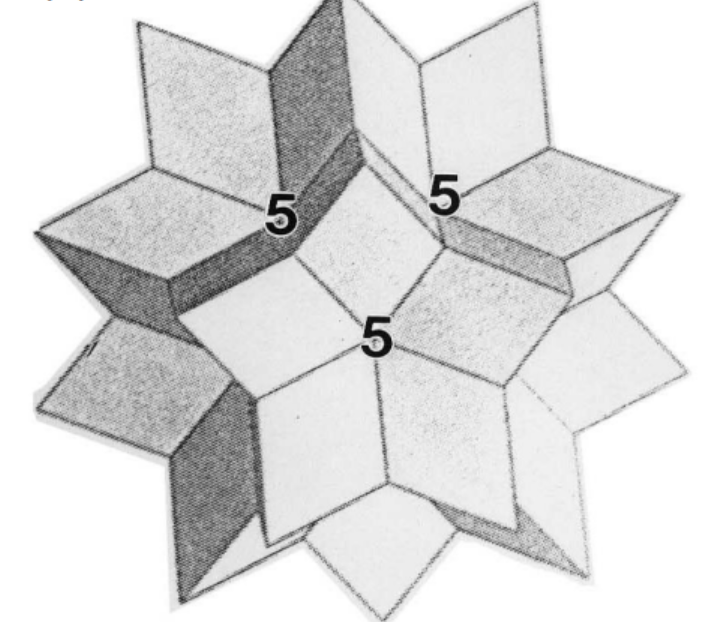
准晶:介于晶体和非晶体之间。准晶体具有与晶体相似的长程有序的原子排列,但是准晶体不具备晶体的平移对称性。因而可以具有晶体所不允许的宏观对称性。普通晶体具有的是二次、三次、四次或六次旋转对称性,但是准晶的布拉格衍射图具有其他的对称性,例如五次对称性或者更高的六次以上对称性。
晶体具有如下基本特征:
晶体的主要特性都源自微观质点的规则排列。
- 对称性:在某些特定方向上各向同性(相同的性质在不同地方有规律地重复出现)
原因:晶体内部质点高度有序排列
反映:方向上旋转对称,微观上平移对称(所以有空间点阵) - 自范性(子限性):晶体自发形成封闭的几何多边形外形。
- 均一性:粒子周期性重复排列,呈现出的各项宏观性质相同。
- 各向异性:晶体内部粒子在不同的方向有不同的排列,所以不同方向展现出不同的性质。
- 稳定性:粒子的规则排列降低晶体内能,处于稳定状态。稳定性体现在晶体具有固定的熔点。
2. 晶体结构
常见晶体很多是多晶,而且内部含有大量取向不同的晶粒和缺陷。
而且晶体内部含有很多规则重复排列的结构单元。
为了研究晶体中质点的排列规律性,将常见晶体视作没有缺陷的理想晶体,又把理想晶体内部周期重复的最小结构单元提取出来,抽象成几何点——阵点。
空间点阵(点阵):阵点在三维空间规则排列的阵列。
晶格(空间格子):用平行线连接阵点后得到的用来描述原子或原子团在晶体中排列方式空间几何格架。
晶体结构=空间点阵(14种布拉菲点阵)+基元(对应的物理实体:原子或原子团)
单胞、7大晶系、14布拉菲点阵Unit cell、Crystal System、Bravais Lattices
单胞Unit Cell
晶胞:从晶格中选出一个能完全反应晶格特征的最小几何单元。
三维晶胞是由轴 a、b、c 和轴间角α、β γ定义的平行六面体。几何考虑表明,只有 7 种可能的唯一晶格参数,导致 7 个可能的晶胞的组合形状——七大晶系。
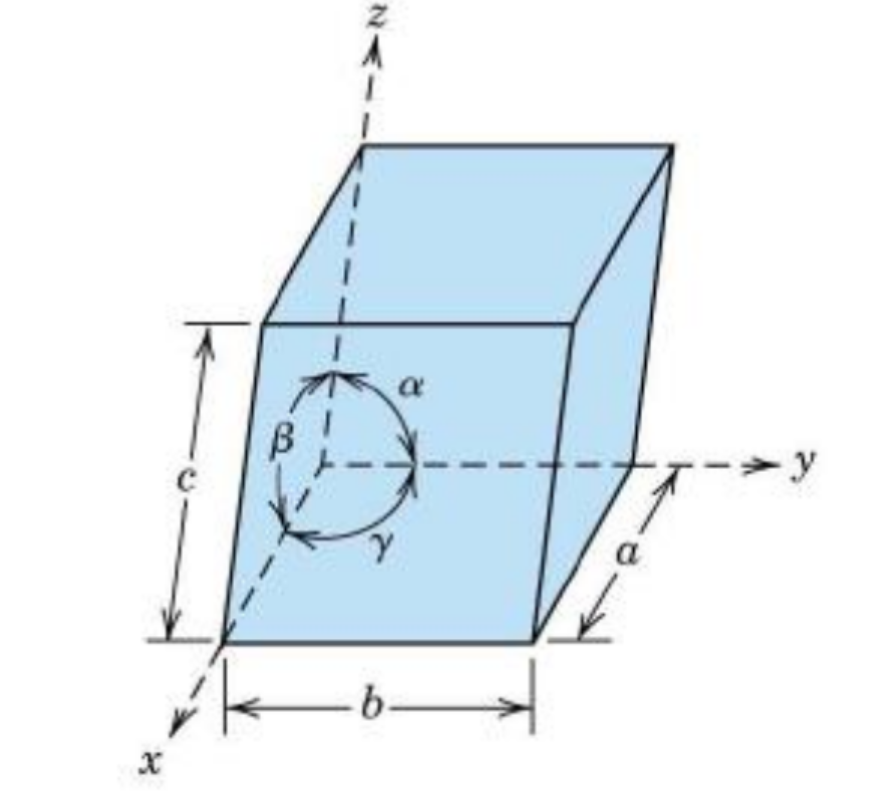
七大晶系Crystal System
7大晶系基于 7 个独特晶胞形状。
每个晶系和相应的晶胞都由不同从晶胞参数的组合定义:a、b、c和α、β、γ


布拉菲点阵Bravais Lattices
7 种可能的晶体系统 + 4 种可能的放置位点→ 14 个晶格 (Bravais Lattices)
4种点阵:
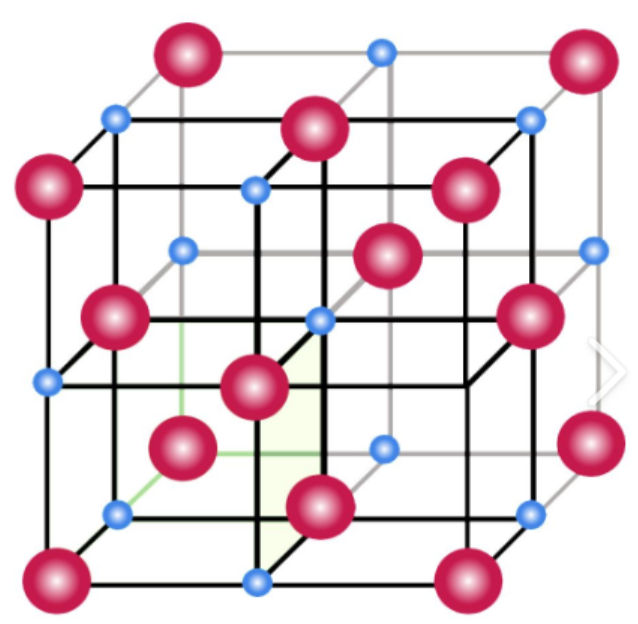
- 简单点阵P:只在六面体八个顶点分布阵点
- 体心点阵I:中心还有阵点
- 底心点阵A、B或C:只在一组对应面中心有阵点
- 面心点阵F:在所有对应面中心有阵点
后3种有心点阵统称为复杂点阵。
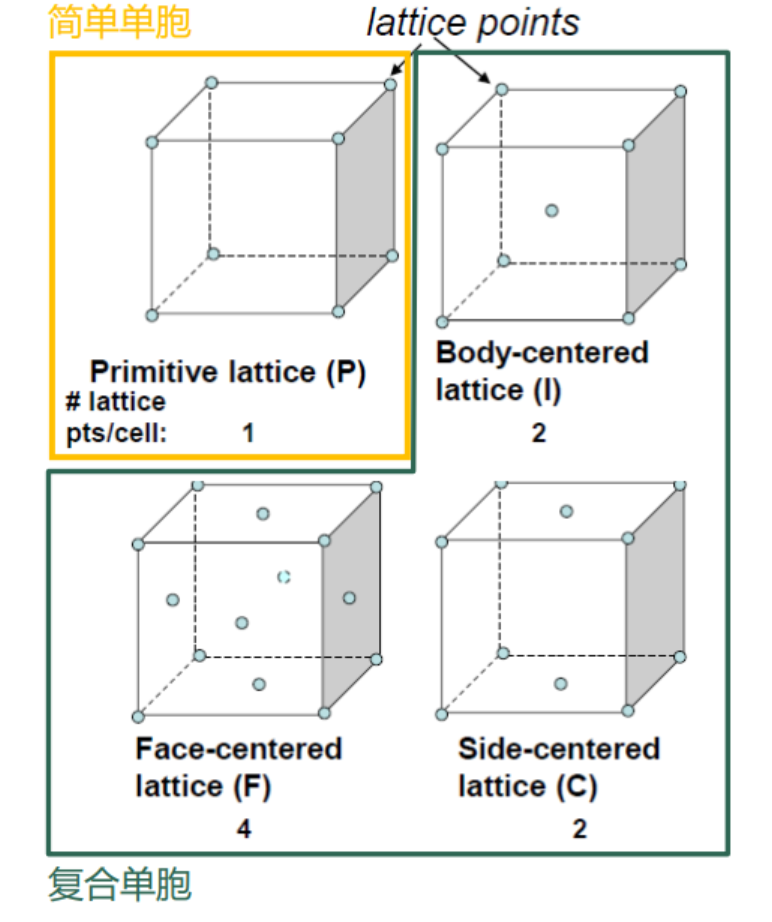
4(placements) × 7(Crystal systems) = 28→14(Bravis lattice) 【实际发现很多点阵不存在,而且有相互等效的点阵】
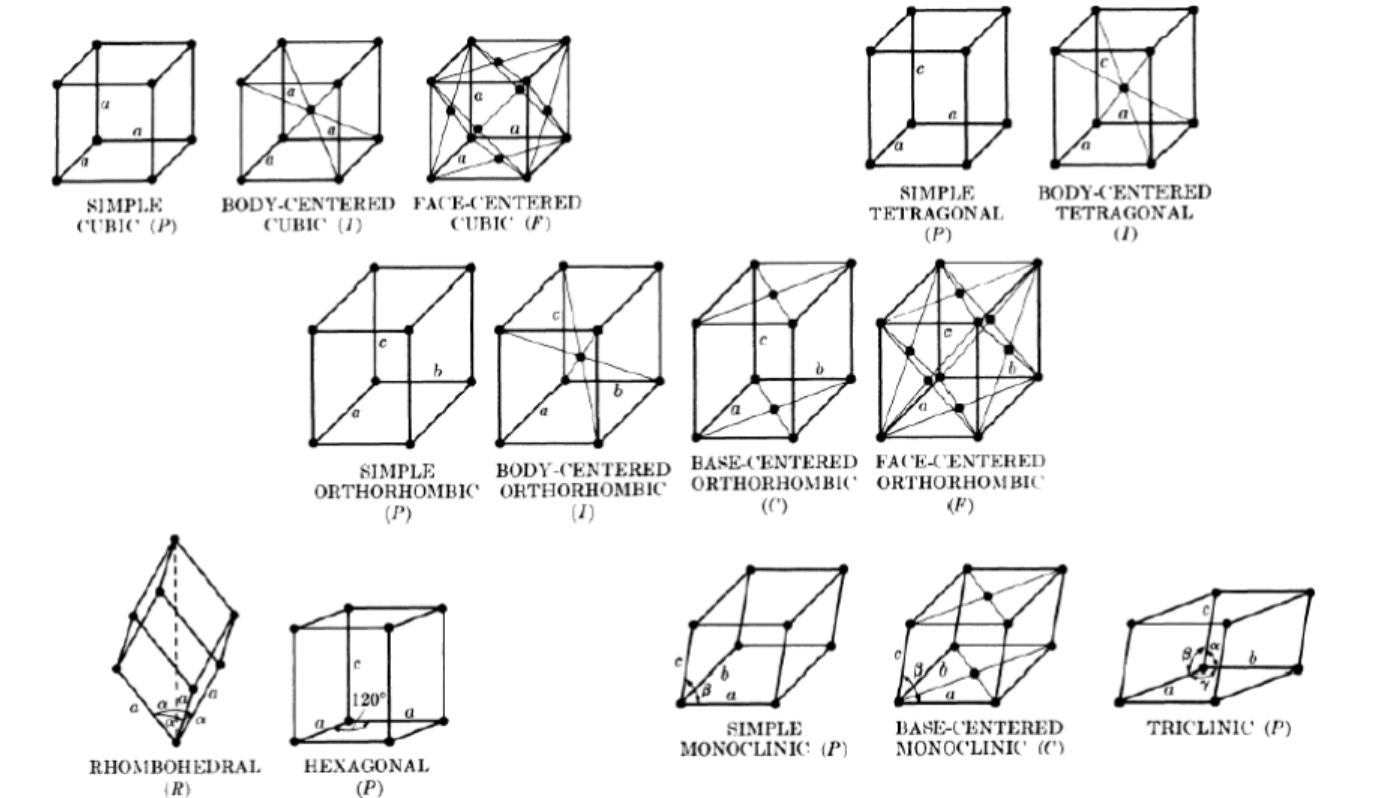
晶向(族)、晶面(族)、晶带轴Crystallographic Directions、Crystallographic Planes、Zone Axis
晶向Crystallographic Directions
空间中某一点的指标,可以从原点作到该点的向量r,向量r可以用基础矢量a,b,c表示: r = u a + v b + w c \bold r=u\bold a+v\bold b+w\bold c r=ua+vb+wc,这里u,v,w是阵点的坐标,也称为晶向指数(可正可负可为零)。
晶向指数建立方法如下:
- 建系
- 过原点作直线OP平行于待求晶向,确定出P的三坐标
- 化整,加方括号:[uvw]为待定晶向的晶向指数(负数在指数上方加一负号)
晶向指数性质:
- 一个晶向指数代表所有方向一致、相互平行的晶向
- 两晶向平行但是方向相反:晶向指数数字相同,符号相反
- 晶向族:原子排列状况相同,但是空间位向不同的各个晶向,用
<uvw>表示(晶向指数数字相同,符号不同)。
比如<121>:[121][112][211][]… - 立方晶系中,改变晶向指数的数字顺序,原子排列状况完全相同,都属于一个晶向族。
晶面Planes in Crystals
晶体(或晶格)可以被认为是一堆平行原子层(或晶格平面)重复固定距离 (D)
可以绘制无限的平行平面集每个晶体都有独特的原子分布,平面密度和平面间距 (D)
这些平面可以使用 Miller 索引系统彼此索引并区分
晶面指数用3个整数+圆括号(hkl)表示。
晶面指数建立方法如下:
- 建系,O选在离待定晶面最近的阵点上
- 求待定晶面在三个坐标轴上的截距值(若平行,则截距值为∞;若与负方向相截,则截距值为负数)
- 求截距值的倒数
- 化为互质,加圆括号:(hkl)为待定晶面的晶面指数(负数在指数上方加一负号)
晶面指数性质:
- 一个晶面指数代表一组相互平行的晶面,经过所有阵点
- 平行晶面:晶面指数相同/数字相同,符号相反
- 晶面族:晶面上原子排列状况相同,晶面间距相同但是空间位向不同的各组晶面,用
{hkl}表示(晶面指数数字相同,符号不同)。
比如{110}:
( 110 ) ( 1 ˉ 10 ) ( 1 1 ˉ 0 ) ( 1 ˉ 1 ˉ 0 ) (110)(\bar110)(1\bar10)(\bar1\bar10) (110)(1ˉ10)(11ˉ0)(1ˉ1ˉ0)
( 101 ) ( 1 ˉ 01 ) ( 10 1 ˉ ) ( 1 ˉ 0 1 ˉ ) (101)(\bar101)(10\bar1)(\bar10\bar1) (101)(1ˉ01)(101ˉ)(1ˉ01ˉ)
( 011 ) ( 0 1 ˉ 1 ) ( 01 1 ˉ ) ( 0 1 ˉ 1 ˉ ) (011)(0\bar11)(01\bar1)(0\bar1\bar1) (011)(01ˉ1)(011ˉ)(01ˉ1ˉ) - 立方晶系中,相同指数的晶面晶向互相垂直
六方晶系中,三轴指数和四轴指数的相互转化
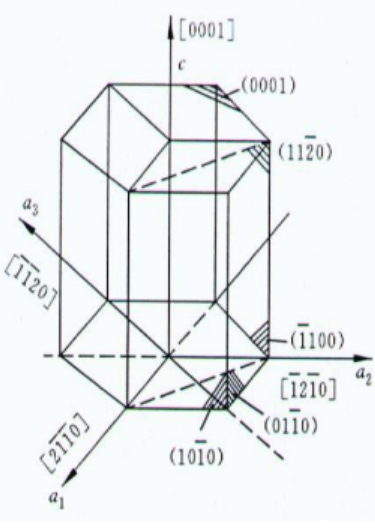
三轴指的是 a 1 , a 2 , c a_1,a_2,c a1,a2,c三轴。
四轴指的是 a 1 , a 2 , a 3 , c a_1,a_2,a_3,c a1,a2,a3,c四轴
晶向指数的转化
三轴晶向指数:[UVW]
四轴晶向指数:[uvtw]
u+v+t=0,W=w
用三轴表示和用四轴表示的是同一条直线:
U a 1 + V a 2 + W z = u a 1 + v a 2 + t a 3 + w z Ua_1+Va_2+Wz=ua_1+va_2+ta_3+wz Ua1+Va2+Wz=ua1+va2+ta3+wz
U a 1 + V a 2 = u a 1 + v a 2 + ( u + v ) ( a 1 + a 2 ) Ua_1+Va_2=ua_1+va_2+(u+v)(a_1+a_2) Ua1+Va2=ua1+va2+(u+v)(a1+a2)
U a 1 + V a 2 = u a 1 + v a 2 + u a 1 + u a 2 + v a 1 + v a 2 = 2 u a 1 + 2 v a 2 + u a 2 + v a 1 Ua_1+Va_2=ua_1+va_2+ua_1+ua_2+va_1+va_2=2ua_1+2va_2+ua_2+va_1 Ua1+Va2=ua1+va2+ua1+ua2+va1+va2=2ua1+2va2+ua2+va1
U = 2 u + v , V = 2 v + u U=2u+v,V=2v+u U=2u+v,V=2v+u
晶面指数的转化
三轴晶向指数:(hkl)
四轴晶向指数:(hkil)
i=-h-k
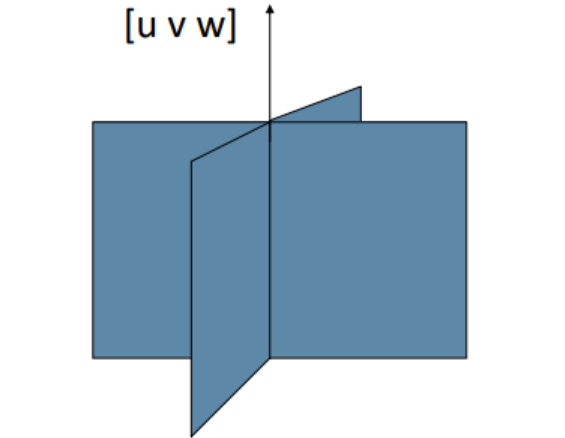
晶带轴Zone Axis
满足[u v w]与所有晶面法线垂直 h u + k v+l w = 0 (晶带轴定律)
一个晶带轴含有无数个晶面,但是只有低指数晶面有实际意义。
求解晶带轴:
已知两个晶面,求过这两个晶面的晶带轴。
两个晶面的晶面指数为 ( h 1 , k 1 , l 1 ) , ( h 2 , k 2 , l 2 ) (h_1,k_1,l_1),(h_2,k_2,l_2) (h1,k1,l1),(h2,k2,l2),那么两个晶面的法线的晶向就是 [ h 1 , k 1 , l 1 ] , [ h 2 , k 2 , l 2 ] [h_1,k_1,l_1],[h_2,k_2,l_2] [h1,k1,l1],[h2,k2,l2],用向量叉乘求同时垂直这两个法线的直线的晶向:
( i j k h 1 k 1 l 1 h 2 k 2 l 2 ) = ( k 1 l 1 k 2 l 2 ) i − ( h 1 l 1 h 2 l 2 ) j + ( h 1 k 1 h 2 k 2 ) k = ( k 1 l 2 − k 2 l 1 ) i + ( l 1 h 2 − l 2 h 1 ) j + ( h 1 k 2 − h 2 k 1 ) k \begin{pmatrix} i & j& k \\ h_1& k_1& l_1\\ h_2& k_2 & l_2 \end{pmatrix}\\= \begin{pmatrix} k_1& l_1\\ k_2 & l_2 \end{pmatrix}i-\begin{pmatrix} h_1& l_1\\ h_2& l_2 \end{pmatrix}j+\begin{pmatrix} h_1& k_1\\ h_2& k_2 \end{pmatrix}k\\ =(k_1l_2-k_2l_1)i+(l_1h_2-l_2h_1)j+(h_1k_2-h_2k_1)k ih1h2jk1k2kl1l2 =(k1k2l1l2)i−(h1h2l1l2)j+(h1h2k1k2)k=(k1l2−k2l1)i+(l1h2−l2h1)j+(h1k2−h2k1)k
晶体的对称性、空间群Symmetry of Crystal、Space Group
晶体的对称性Symmetry of Crystal
对称操作(Symmetry operation):
能够使对称物体(或图形)中的各个相同部分间做有规律重复的变化动作。
对称要素(Symmetry elements):
进行对称变换时所凭借的几何要素——点、线、面等。
宏观对称性
-
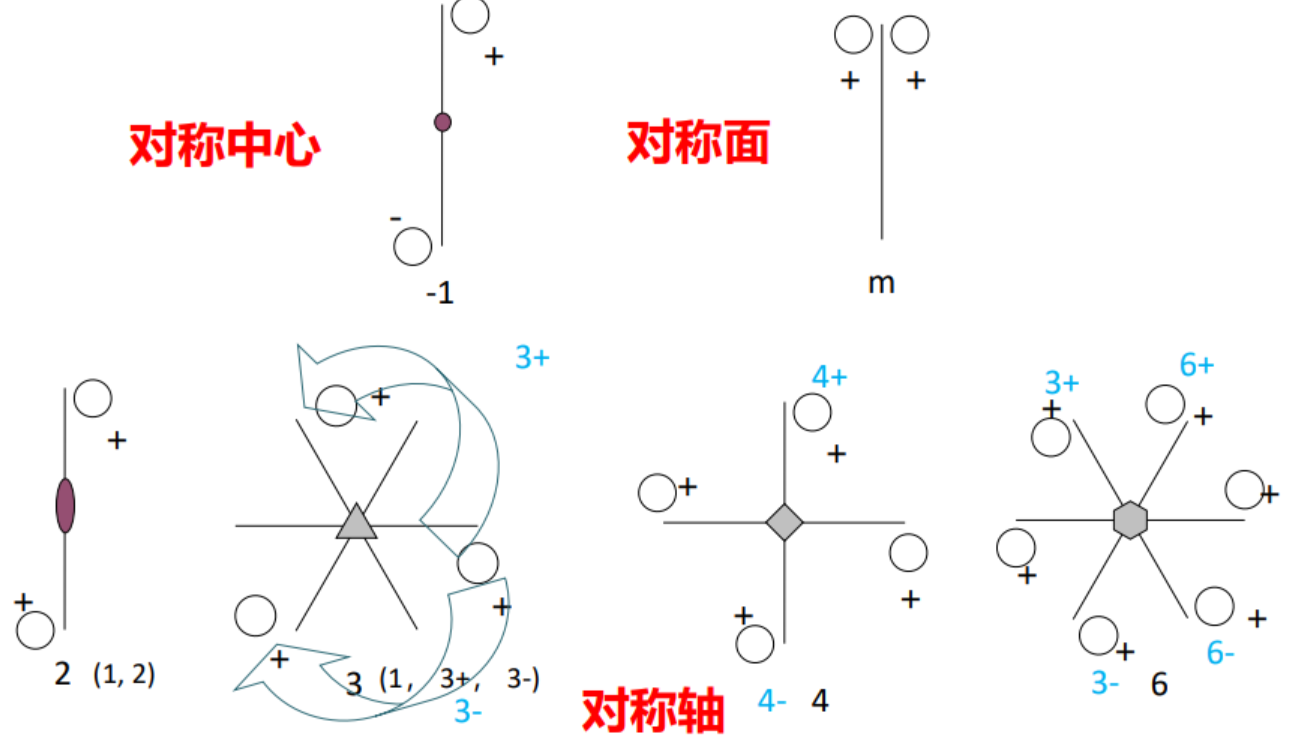
对称中心 (Symmetry center,国际符号: 1 ˉ \bar 1 1ˉ):对称操作为对这个点的倒反
-
对称面(Symmetry plane, 国际符号: m):对称操作为对这个面的反映
-
对称轴(Symmetry axis, 国际符号:n):对称操作为围绕此直线旋转
- 晶体对称定律:晶体中,只可能出现轴次为1、2、3、4、6次的对称轴
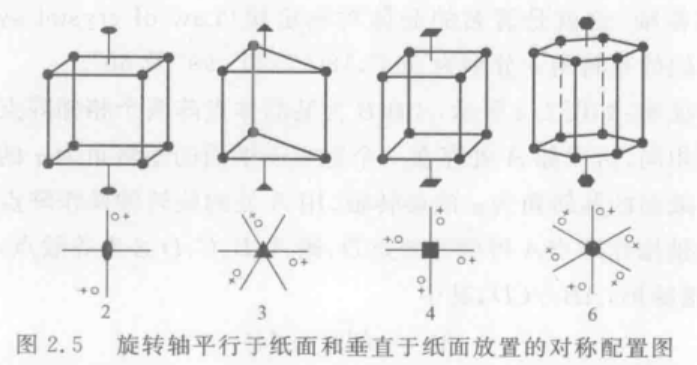
这里的空心圆圈表示一般等效点的位置,”+“表示此点位于纸面之上。
-
倒反轴(Rotation-inversion axis, 简称反轴,国际符号: n ˉ \bar n nˉ)(复合对称操作,由一个旋转轴加轴上的一个对称中心组成)

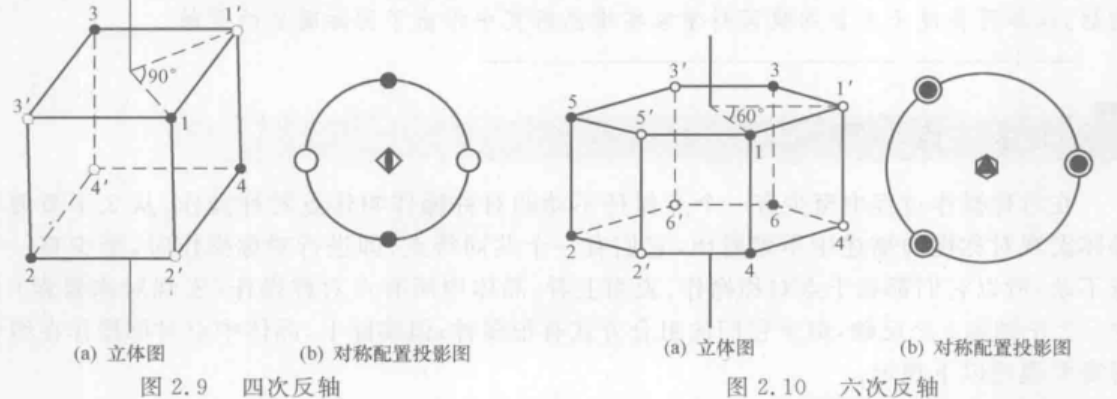
实心点和空心点表示不同高度的点。数字‘表示旋转后的点,再进行对称中心
微观对称性
1.平移轴(Translation axis)
平移轴为一直线,晶体结构沿该直线移动一定距离可使晶体复原。
空间点阵中任意一个行列都是平移轴。
晶体复原:晶体沿着空间点阵中任意一个行列移动一个或多个阵点间距都可以让每一个阵点和相同的阵点重合。
2.螺旋轴(Screw axis)= 平移 + 旋转
包括一个n次旋转轴和与此平行并有一定移距(τ=s/n)的平移操作。操作顺序可以互换。
n为旋转轴的轴次,根据晶体对称定律,n=1,2,3,4,6;s≤n,且只能取1,2,3,4,6。
螺旋轴根据其轴次和平移移距的不同可以分为12种,其国际符号为:

大的数字n表示轴次n,数字角标i表示在此轴上移动i个原子间距。
其中 1 1 1_1 11表示旋转一周并在轴上移动一个原子间距,相当于没动,故去掉这种情况,实际有效的螺旋轴只有11种。
下面给出螺旋轴的投影配置图,所有旋转都用右旋替代。
二次螺旋轴
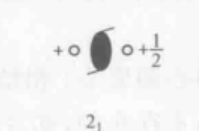
二次螺旋轴先把阵点(用小空心圆代替)从左旋到右,再沿着轴往上挪了1/2个原子间距,所以右边对应的小空心圆比纸面高了+1/2。
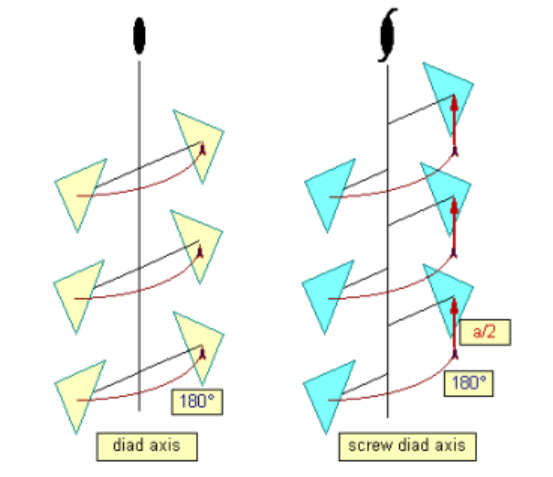
三次螺旋轴
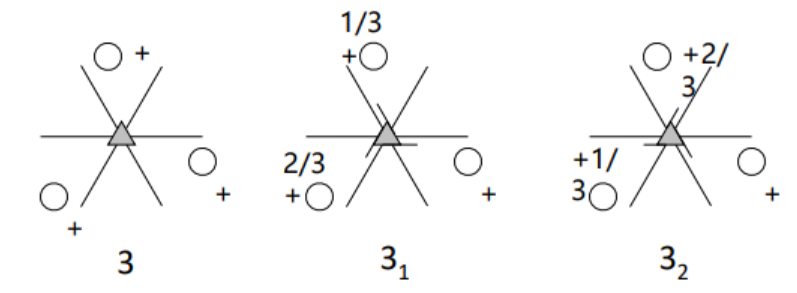
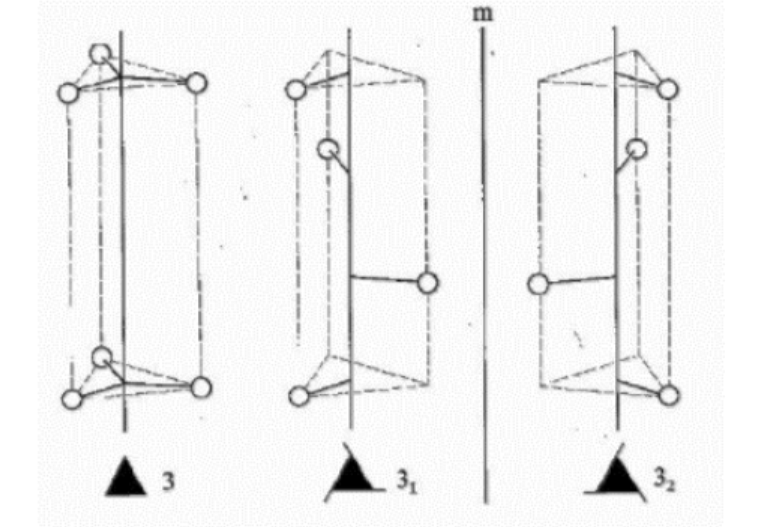
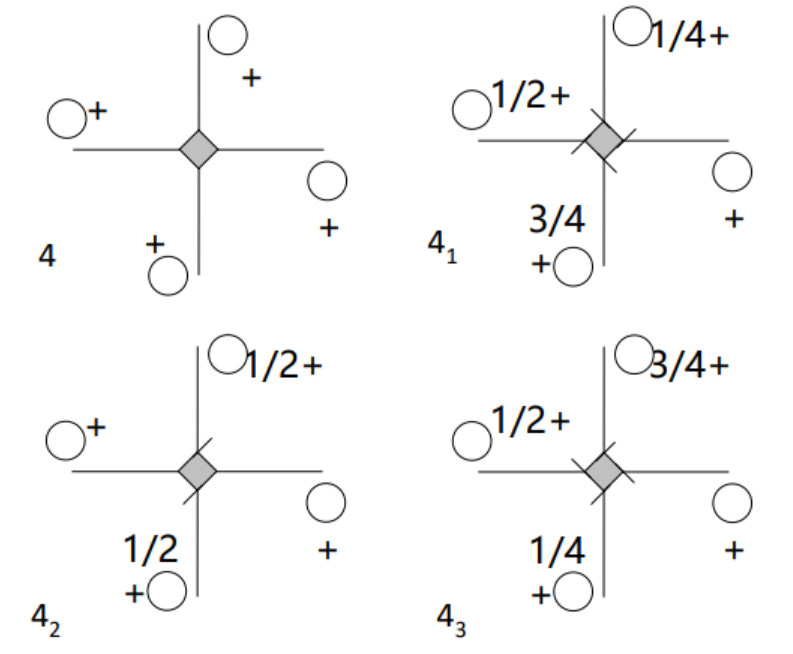
4次螺旋旋转轴
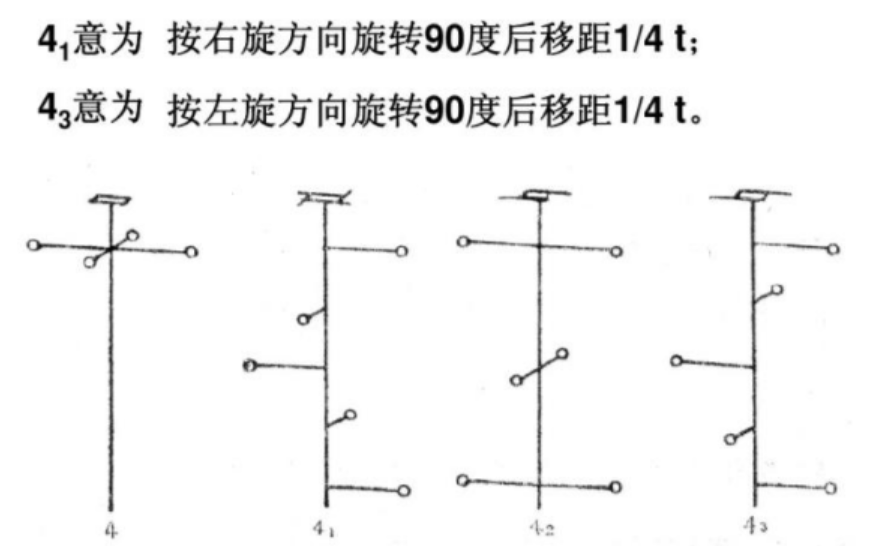
6次螺旋旋转轴
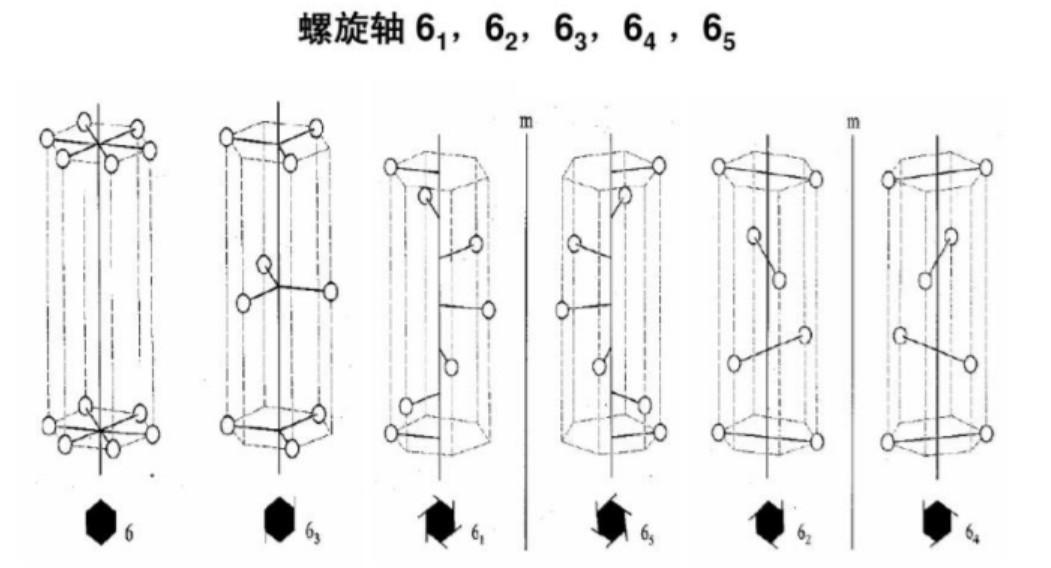
3.滑移面(Glide plane)= 平移 + 镜面
镜面反映+沿着平行于镜面的平移,平移方向可为单胞的某一棱边a、b、c〔轴向滑移a、b、c),或单胞的面或体对角线方向(对角滑移n或d〕;量为该周期的1/2。

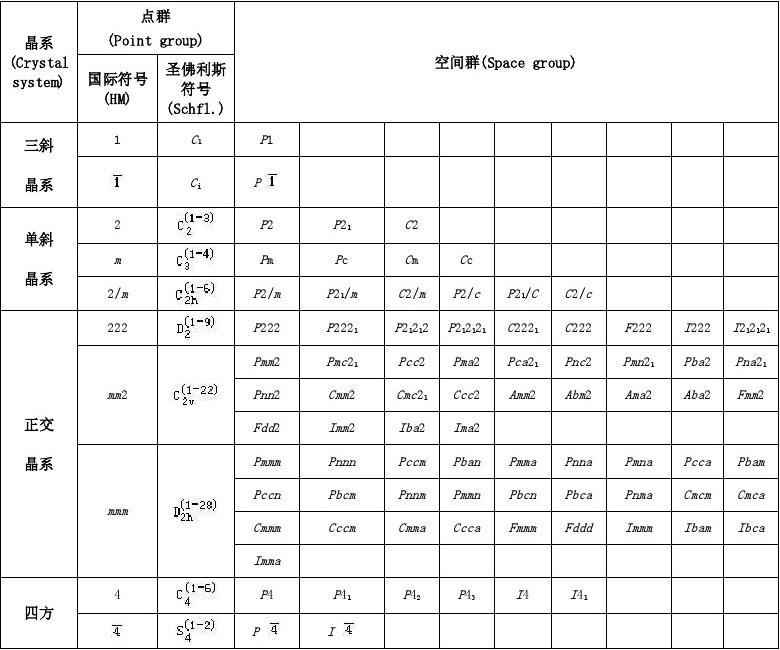
空间群Space Group
空间群:晶体学种所有对称要素(宏观对称+微观对称)组合的所有可能性构成的集合。
能使晶体结构复原的所有对称变换的集合。
空间群符号
L
S
1
S
2
S
3
L_{S1S2S3}
LS1S2S3
运用以下规则,可以从对称元素获得空间群符号。
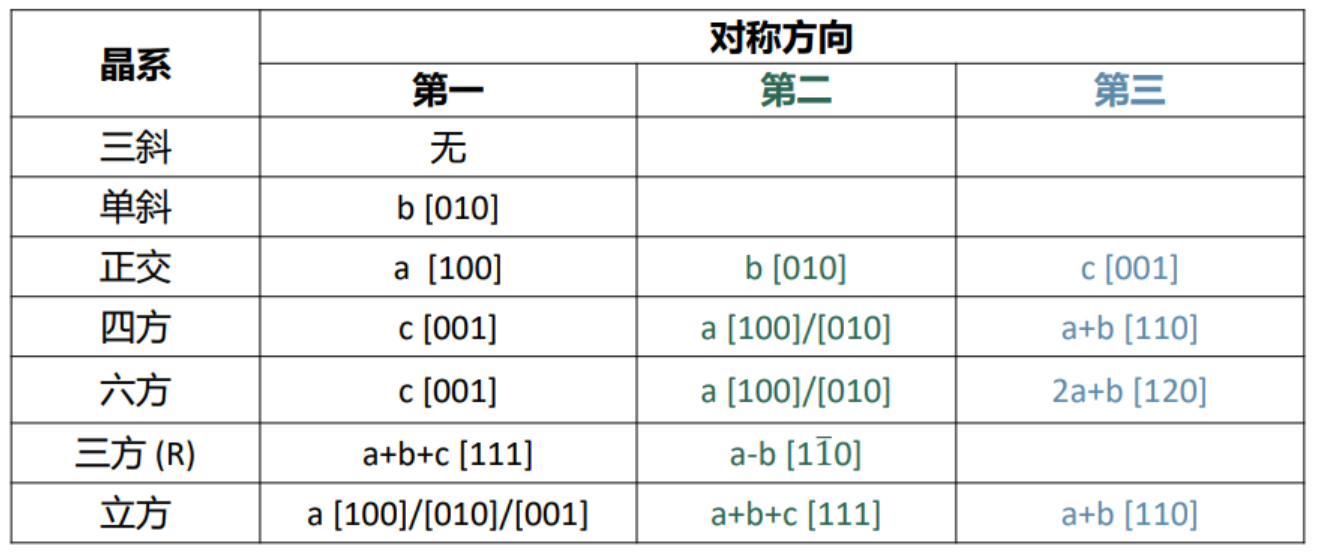
- 第一字母(L)是点阵描述符号,指明点阵带心类型: P, I, F, C, A, B。
- 其余三个符号(S1S2S3)表示在特定方向(对每种晶系分别规定)上的对称元素。后一部分与点群的国际符号基本相同,不同的是那三个特定方向上的对称要素取自晶胞中对应方向上对称程度最高的那种对称要素。
- 如果没有二义性可能,常用符号的省略形式 (如Pm,而不用写成P1m1)。
- 由于不同的晶轴选择和标记,同一个空间群可能有几种不同的符号。如P21/c,如
滑移面选为在a方向,符号为P21/a;如滑移面选为对角滑移,符号为P21/n。