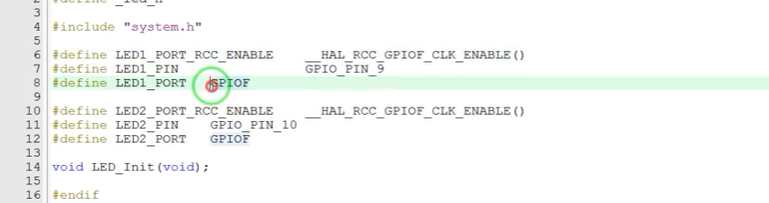
YOLO(You Only Look Once)是一个标志性的目标检测模型,可以快速分类并定位图像中的多个对象。本文总结了YOLO模型中所有关键的数学操作。
第一步:定义输入
要使用YOLO模型,首先必须将RGB图像转换为448 x 448 x 3的张量。

我们将使用简化的5 x 5 x 1张量,这样数学计算会更简洁一些。
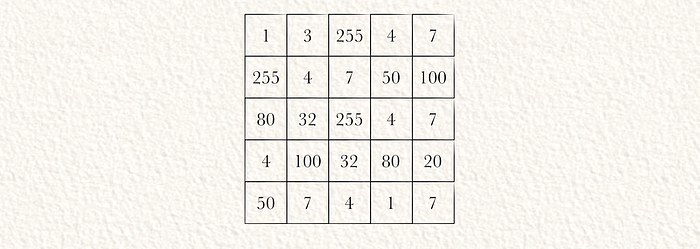
第二步:层归一化
神经网络通常在归一化数据上表现更好。我们可以通过首先计算矩阵中的平均值(µ)来归一化输入。
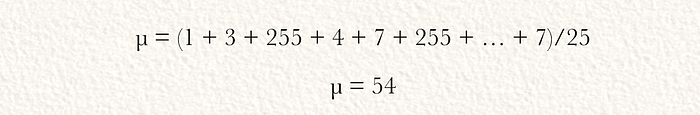
接下来,可以计算所有元素与平均值的绝对差值。
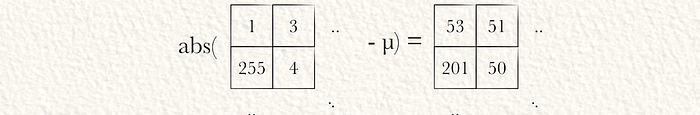
然后,可以通过对前一部分的结果中的所有值进行平方,将它们相加,除以值的数量,并计算平方根来计算标准差。
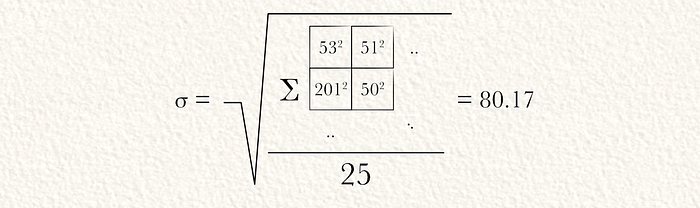
一旦计算出标准差,可以通过减去均值并除以标准差来对输入进行层归一化。

均值和标准差可用于归一化输入值。均值是输入图像的平均值,标准差是原始图像中值的分布宽度。通过减去均值并除以标准差,我们“归一化”了图像。
注意:我们计算了层归一化。原始的YOLO论文使用批归一化,它在一个批次的不同图像之间归一化相同的值。这两者之间的概念差异可以忽略不计。
第三步:卷积
现在我们的输入已经归一化,我们将其通过卷积网络。我们将YOLO理想化为具有两个内核的单卷积层。
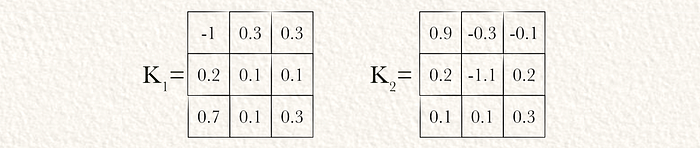
为了确保输出张量具有与输入相同的空间维度,我们在归一化输入上应用0填充。
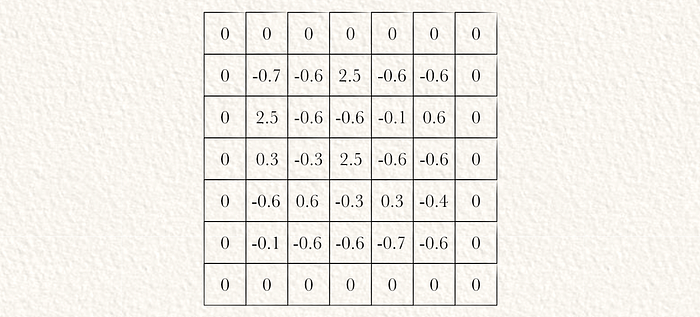
然后可以通过元素乘法(⊙)和累加求和(Σ)将两个内核卷积到图像上。
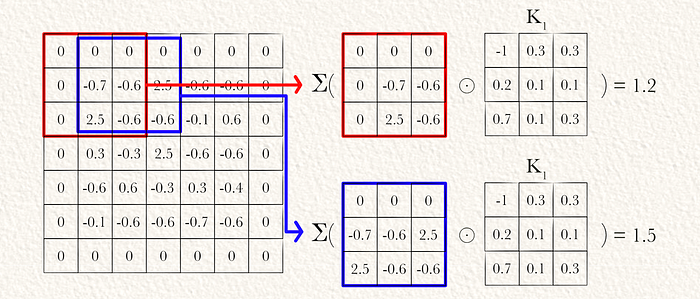
在输入上卷积两个内核后,我们得到两个大小相等的数组。通常将其表示为3D张量,不同的内核存在于称为“过滤器”或“内核”维度的维度中。
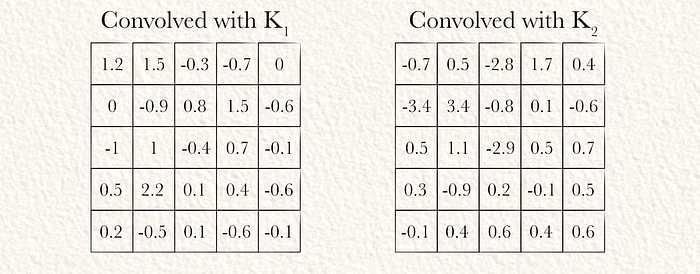
第四步:最大池化
现在我们对输入进行了卷积,可以应用最大池化。在此示例中,我们用2 x 2的窗口和步幅为2对每个卷积矩阵进行最大池化。我们也最大池化部分区域。在这种情况下,我使用了一个实现最大池化的函数,如果所有值都为负,则将值设置为零。实际上,我认为这几乎没有影响。
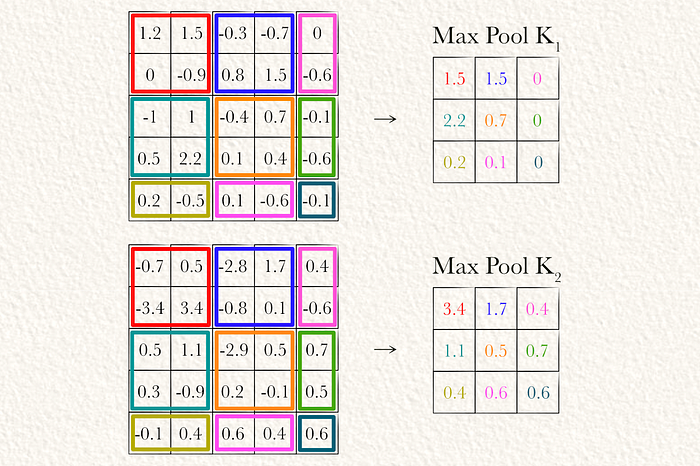
最大池化观察输入的一个子集,并只保留每个子集的最大值。
第五步:非线性激活
几乎所有的机器学习模型,包括YOLO,都在模型中使用非线性“激活函数”。由于之前所有的数学运算都是线性的(乘法和加法),所以之前的步骤只能模拟线性关系。添加一个将模型中的值非线性映射的函数,可以让模型学习非线性关系。在此示例中,我们使用sigmoid激活函数,但ReLU更为常见。
注意:在最大池化之后应用激活函数效率更高一些。
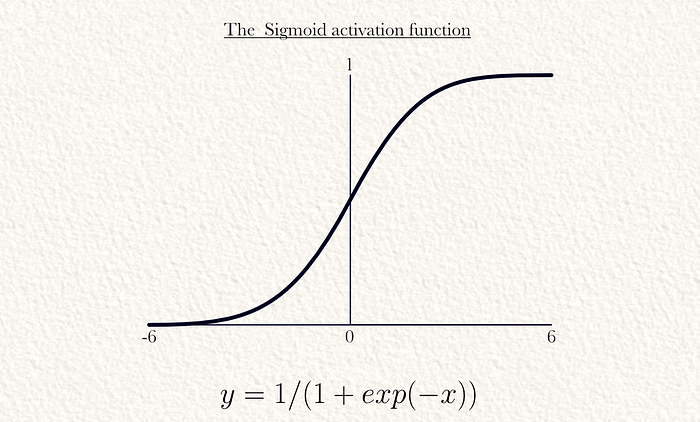
这个函数可以按元素应用于所有最大池化的矩阵。
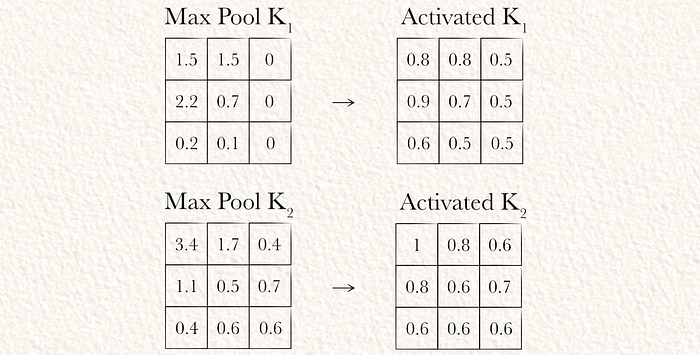
第六步:展平
现在输入图像已经被过滤成一个更适合最终建模任务的抽象表示(实际上是通过几个卷积层,而不是本示例中的一个卷积层),可以通过展平将其转换为一个向量。
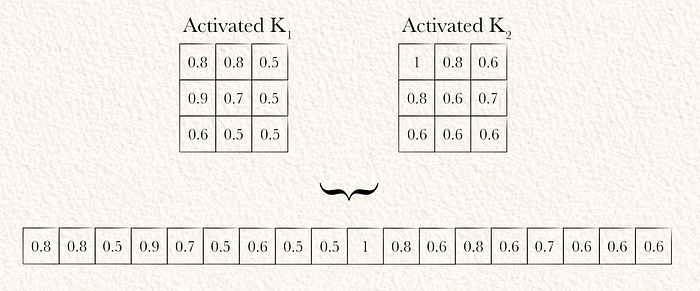
第七步:输出投影
可以使用一个密集网络(即矩阵乘法)将展平的矩阵投影到最终输出。YOLO的最终输出包括SxSxC类预测和SxSxBx5个边界框预测。因此,输出的形状必须为SxSx(C+Bx5)。假设在前一步展平的输出长度为L,则密集网络的权重矩阵形状必须为Lx(SxSx(C+Bx5))。
在这个示例中,我们假设S为1,C为2,B为1。L是展平向量的长度,为18。因此,权重矩阵的形状应为18 x 7。
注意:用`表示转置矩阵。
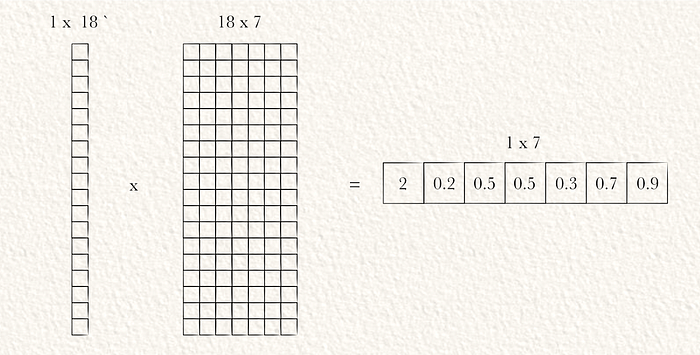
每个网格单元的类概率之和应为1。因此,每个网格单元的预测类概率需要进行softmax。

每个两个类概率中的一个作为e的指数,这些值除以两个值的总和作为e的指数。e是欧拉常数,值为2.718,具有某些指数特性,因此在此上下文中很常用。
第八步:推理
YOLO的最终输出(在此示例中为7元素长的向量)已经计算完成。现在我们可以使用这些值生成最终的推理。由于S=1,只有一个网格单元。由于B=1,只有一个边界框。由于C=2,有两个类预测。
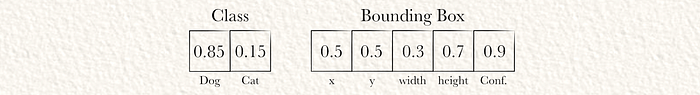
YOLO预测网格单元(在这种情况下是整个图像)包含一只狗。边界框距离左墙和顶墙各50%。宽度是网格单元宽度的30%,高度是网格单元高度的70%。此外,YOLO有90%的置信度认为这是一个好的边界框。
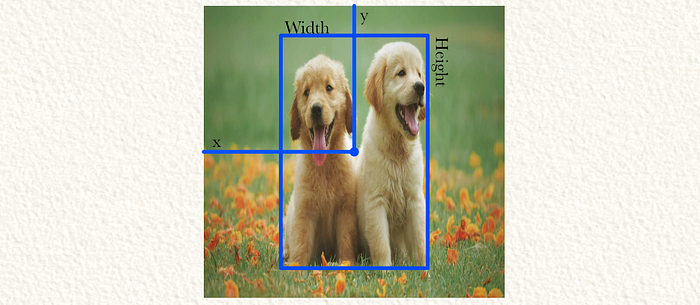
在一个不那么简单的示例中,网格有四个单元(S=4),每个单元一个边界框:
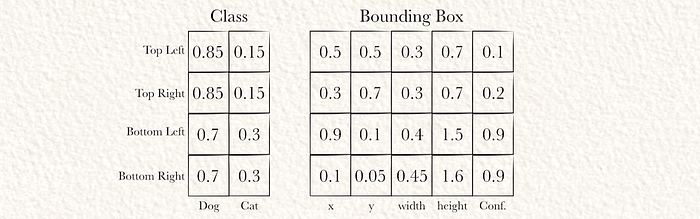
一个不那么简单的输出示例 左上和右上单元的置信度太低,因此不使用边界框。使用了其他两个。请注意,高度(和宽度)可以大于1,因为边界框可以是网格单元高度的倍数。

结论
就这样。在本文中,我们介绍了计算YOLO输出的主要步骤:
-
定义输入
-
归一化输入
-
应用卷积
-
应用最大池化
-
非线性激活
-
展平
-
投影到输出形状