图 1.多元线性回归与简单线性回归
一、说明
线性回归从一维推广到多维,这与单变量线性回归有很多不同,情况更加复杂,而在梯度优化也需要改成向量梯度,同时,数据预处理也成了必要步骤。
二、综述
多元线性回归是简单线性回归的一种广义形式,它使用多个自变量来预测因变量。根据表 1,使用发动机尺寸 x_1、x_2 的气缸数和燃料消耗量x_3来估计排放的 CO2 气体 (y) 是多元线性回归。多元线性回归公式如公式 1 所示。
多元线性回归的方程 1:
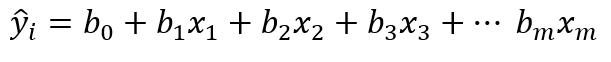
在等式 1 中,m 指的是自变量的数量,训练模型的过程类似于简单的线性回归,不同之处在于,这里我们不是确定 a 和 b,而是找到 m+1 个合适的数字(b_0、b_1、...b_m)。使用多元线性回归可以显示自变量(x_1、x_2、x_3 等)的有效性x_m) 估计因变量 (y) 并获得每个自变量的变化在改变因变量中的影响。
表 1 显示了多元线性回归中的自变量和因变量:

图 1.I个因变量和因变量
如前所述,数据不能用高于三个维度的维度来表示,但可以针对每个自变量 (x_i) 绘制目标数据或标签。我们在本章中介绍的数据有七个特征或特征,如图 2 所示,CO2 气体的因变量 (CO2_Emissions) 与三个特征(自变量)的比较。
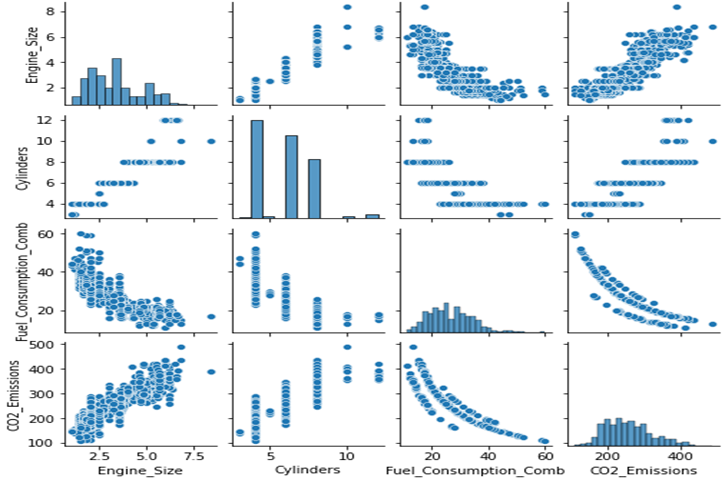
图 2.为每个特征绘制因变量数据
可以看出,数据显示相对分散,它表明因变量 (y) 的输出是几个自变量的函数,换句话说,它不受一个变量的影响,几个变量在确定输出值方面发挥作用。
我将为一个名为 “50 Startups Data” 的数据集编写一个代码来解析多元线性回归,该数据集适用于多元线性回归的任务。根据 Kaggle 网站:
我们在这里看到的数据集包含有关 50 家初创公司的数据。它有5列:“研发支出”,“管理”,“营销支出”,“状态”,“利润”。
前 3 列表示每家初创公司在研发上花费了多少,他们在营销上花费了多少,以及他们在管理成本上花费了多少,状态列表示初创公司所在的州,最后一列表示初创公司获得的利润。
如果您想访问代码和数据集,请打开我的 GitHub 仓库,并下载“50_Startups.csv”数据集。
首先,我们应该导入一些需要的库:
三、包含库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression然后我们应该用 pandas 加载 csv 数据集:
四、加载数据集
df = pd.read_csv('./Datasets/50_Startups.csv')
df.head()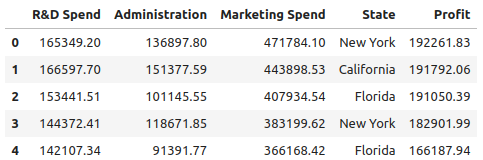
图 3. 前 5 行数据
print(df.dtypes)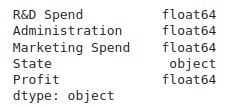
图 4. 列或特征的类型
我们应该将 “object” 类型转换为 “category” 类型,在 pandas 中使用此命令是可能的:
df['State'] = df['State'].astype('category')
print(df.dtypes)
图 5. 将对象转换为类别
这是清理和预处理数据的时间:
4.1. 检查并处理缺失值
我们可以使用以下命令在 pandas 中看到 null 值:
df.isnull().sum()
图 6. 查看 null 值
如上图所示,我们在第二列中有两个 null 值,在第三列中也有一个 null 值。要查看缺失值,您可以使用另一个名为 Missingno 的出色库。Missingno 是一个 Python 库,用于可视化数据集中的缺失数据。它提供了一种识别模式和了解数据集中缺失值范围的便捷方法。
import missingno as msno
msno.matrix(df)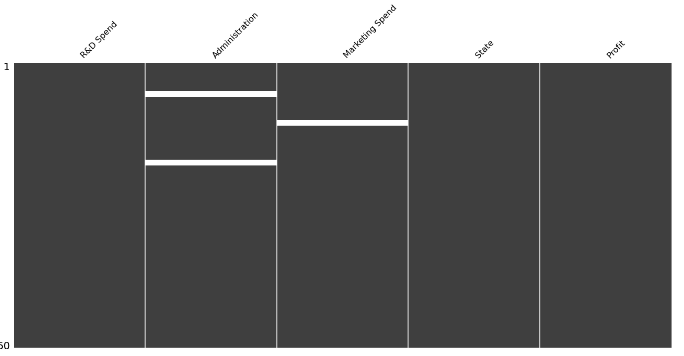
图 7. 缺少用于查找缺失值的输出
您可以使用 fillna() 函数将 pandas DataFrame 中的 NaN 值替换为特定值。用于替换的常见值之一是 median,我将其填充为每列的缺失值。
检查管理功能:
m = df['Administration'].median()
print(f"Median for Administration feature is:", m)
# Median for Administration feature is: 122699.795使用以下命令计算每个特征的缺失值数:
print(df['Administration'].isna().sum())
# 2最后,用这个命令填充它 (fill with median):
df['Administration'].fillna(m, inplace=True)
print(df['Administration'].isna().sum())
# 0我们应该填补另一个功能 (Marketing Spend) 的缺失值:
med_marketing = df['Marketing Spend'].median()
df['Marketing Spend'].fillna(med_marketing, inplace=True)
df['Marketing Spend'].isna().sum()
# 0在用每个特征的中位数填充缺失值后,现在我们再次看到 msno 库的结果:
msno.matrix(df)
图 8. Missing 填充缺失值后无输出
4.2. 编码分类特征
在我解释什么是编码以及如何进行编码之前,请先看一下 DataFrame 的输出:
df.head()
图 9. 编码前的数据输出
在机器学习中,包含非数值的分类变量(特征)很常见。但是,大多数机器学习算法都需要数字输入。为了解决这个问题,我们执行了一个称为 “编码分类特征” 的过程,该过程涉及将这些分类变量转换为机器学习模型可以理解和处理的数字表示。
对分类特征进行编码有几种常用方法:
- One-Hot Encoding:对于每个分类变量,将为每个唯一类别创建一个新的二进制特征。如果存在类别,则二进制特征的值为 1,否则为 0。独热编码扩展了特征空间,但保留了有关类别的信息。One-Hot Encoding 通常使用 pandas 中的函数执行。例如,我们的数据中有一个名为“State”的列,其类别为“New York”、“California”和“Florida”,使用该列将为每个类别创建新列,并根据类别是否存在分配值 1 或 0。因此,结果将包含“State_California”、“State_Florida”和“State_New York”等列,其中的二进制值指示原始“State”列中每列的存在与否。
pd.get_dummies()pd.get_dummies() - Label Encoding:在此方法中,为每个类别分配一个唯一的整数标签。标签的分配方式可以保留类别之间的序号关系(如果有)。我们不需要此方法,因为 State 功能没有任何订单。
这是我们在 Pandas 中使用 One-Hot 编码的方式:
df_encoded = pd.get_dummies(df, columns=['State'], dtype=np.float64)
df_encoded.head()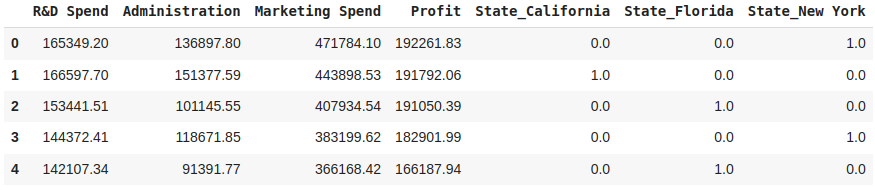
图 10. 对 'State' 功能进行编码后的数据输出
4.3. 更改列的顺序
我们的标签是 Profit,标签通常位于最后一列,代码如下:我们可以按自己喜欢的任何顺序放置列:
df_encoded = df_encoded[['R&D Spend', 'Administration', 'Marketing Spend',
'State_California', 'State_Florida', 'State_New York', 'Profit']]
df_encoded.head()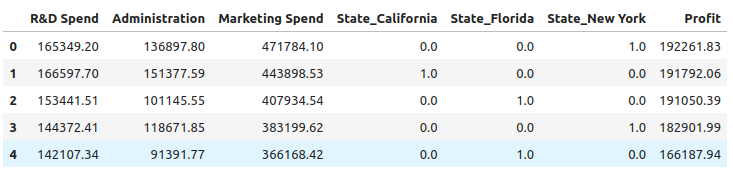
图 11. 重新排序的要素
4.4. 重命名列名称,以便它们可以编码
在数据分析和机器学习中,通常建议避免使用带空格的列名,而是将它们转换为更方便且与编程语言兼容的格式。最常见的方法是将空格替换为下划线或其他合适的字符。
df_encoded.rename(columns={'R&D Spend': 'R&D_Spend',
'Marketing Spend': 'Marketing_Spend',
'State_New York': 'State_New_York'}, inplace=True)df_encoded.head()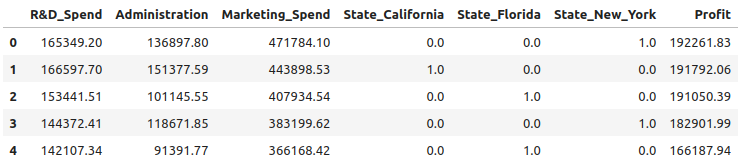
图 12. 重命名的列
五. 异常值的箱形图
异常值是明显偏离数据集中大多数数据的数据点。它们可以是与其他值相比异常大或异常小的观测值。异常值可能由于各种原因而发生,例如测量错误、数据损坏或罕见事件。
在机器学习模型中考虑异常值非常重要,因为它们会对模型的性能和结果产生重大影响。异常值可能会扭曲统计度量,例如平均值和标准差,从而导致估计值有偏差和预测不准确。它们还会影响某些算法的假设,例如线性回归,这些算法假定数据服从正态分布。
识别和可视化异常值的一种常用技术是箱形图(也称为箱须图)。箱形图通过显示四分位数、中位数和潜在异常值来提供数据集分布的可视化摘要。该框表示四分位距 (IQR),其中包含中间 50% 的数据。晶须从框延伸到一定范围内(通常是 IQR 的 1.5 倍)内的最小和最大数据点。超出此范围的数据点被视为潜在的异常值,并绘制为单个点。
import matplotlib.pyplot as plt
fig, axes = plt.subplots(2, 4, figsize=(20, 8))
axes_flat = axes.flatten()
for i, col in enumerate(df_encoded.columns):
ax = axes_flat[i]
ax.boxplot(df_encoded[col])
ax.set_title(col)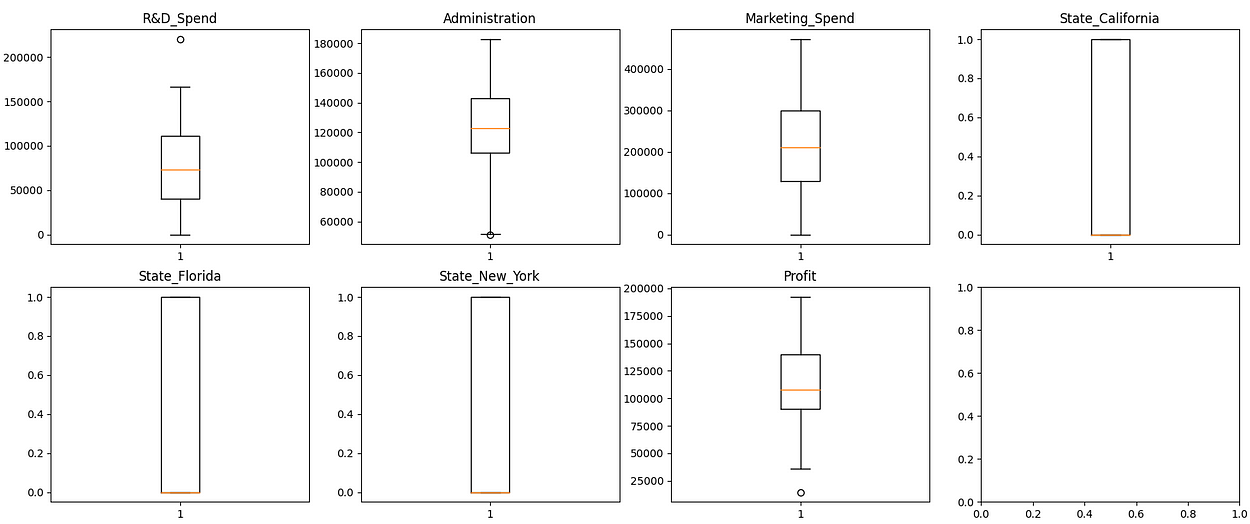
图 13. 用于查找异常值的箱形图
注意:使用独热编码特征时,无需像处理数值特征那样考虑异常值。独热编码特征由二进制值(0 或 1)组成,没有数字分布来评估异常值。独热编码特征不是测量值的大小或偏差,而是关注某个类别的存在或不存在。因此,离群值的概念在 one-hot 编码特征的上下文中是无关紧要的。但是,我为所有特征绘制了箱形图。
有几种方法可以从数据集中删除异常值,其中一种常见且有用的方法称为 IQR,我将在下面解释它:
- 通过从第三个四分位数 (Q3) 中减去第一个四分位数 (Q1) 来计算数据集的四分位数间距 (IQR)。
- 定义下限 (Q1–1.5 * IQR) 和上限 (Q3 + 1.5 * IQR)。
- 删除低于下限或高于上限的任何数据点。
下图显示 IQR 方法的工作原理:
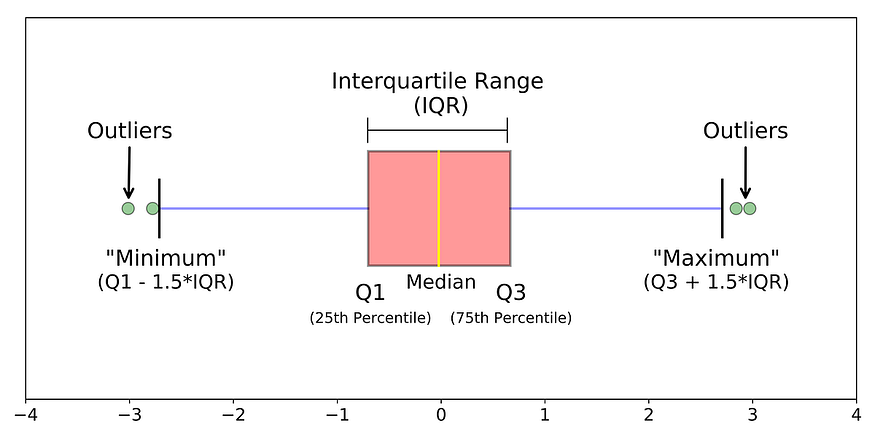
图 14. 用于异常值检测的 IQR 方法
计算 df_encoded 中每列的第一四分位数 (q1)、第三四分位数 (q3) 和四分位距 (iqr)。这有助于确定大多数数据点所在的范围。
q1 = df_encoded.quantile(0.25)
q3 = df_encoded.quantile(0.75)
iqr = q3 - q1根据四分位距计算下限和上限截止值。这些截止值用作确定异常值的阈值。低于 cutoff_low 或高于 cutoff_high 的数据点被视为潜在异常值。
cutoff_low = q1 - (1.5 * iqr)
cutoff_high = q3 + (1.5 * iqr)创建一个布尔掩码,用于标识哪些数据点 df_encoded 属于截止值定义的可接受范围。对于不被视为异常值的数据点,此掩码为 True;对于潜在异常值,此掩码为 False。
mask = (df_encoded >= cutoff_low) & (df_encoded <= cutoff_high)应用布尔掩码以从 df_encoded 中筛选出可能的异常值行。mask.all(axis=1) 检查掩码每行中的所有值是否均为 True,这表示该行中的任何列都不包含异常值。生成的df_filtered仅包含没有异常值的行。
df_filtered = df_encoded[mask.all(axis=1)]用于删除异常值的集成代码如下:
q1 = df_encoded.quantile(0.25)
q3 = df_encoded.quantile(0.75)
iqr = q3 - q1
cutoff_low = q1 - (1.5 * iqr)
cutoff_high = q3 + (1.5 * iqr)
mask = (df_encoded >= cutoff_low) & (df_encoded <= cutoff_high)
df_filtered = df_encoded[mask.all(axis=1)]
df_filtered.head()现在是时候创建一个新的 DataFrame 了,其中包含根据布尔掩码识别为异常值的行 df_encoded。
# see outliers with ~ [~mask.all]
df_outliers = df_encoded[~mask.all(axis=1)]
df_outliers.head()
图 15. 包含离群值的新 DataFrame
六、特征选择/缩减
特征选择或减少与相关性涉及根据特征与目标变量或彼此之间的相关性来识别和选择或减少数据集中的特征。通过检查特征之间关系的强度和方向,这种方法有助于确定与给定任务最相关和信息量最大的特征,从而有可能提高模型性能并降低计算复杂性。
Pearson 相关系数通常用于测量线性相关,其他相关度量可以捕获不同类型的关系。例如:
- 皮尔逊相关系数:它衡量两个连续变量之间线性关系的强度和方向。
- Spearman 相关系数:它评估变量之间的单调关系,它捕获变量之间的任何增加或减少趋势,而不管线性如何。
- Kendall 的 tau:它度量变量之间的序数关联,适用于排名或有序数据。
correlation = df_filtered.corr(method='pearson')
correlation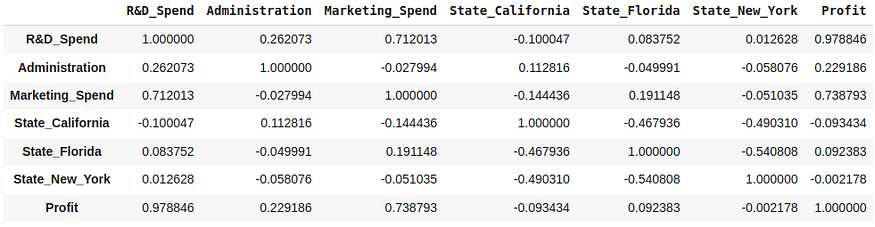
图 16. 特征之间的关联
我们需要知道每个功能对标签 (Profit) 的影响,通过这些代码行我们可以做到这一点:
corr = df_filtered.corr()
corr[['Profit']].abs().sort_values(by='Profit', ascending=False)
图 17. 基于标签的排序相关性
我们想做 Feature selection or reduce with correlation 涉及根据特征与目标变量或彼此之间的相关性来识别和选择或减少数据集中的特征。在本例中,我想删除与标签 (Profit) 相关性较低的特征:
df_copy = df_filtered.copy()
df_copy.drop(['State_California', 'State_Florida', 'State_New_York'], axis=1, inplace=True)
df_copy.head()
图 18. 删除部分特征后的数据集
七、训练测试拆分
在这里,我们分配 X 和 y 变量,其中 X 特征变量具有自变量,y 特征变量具有因变量。
X = df_copy.iloc[:, :-1].values
y = df_copy.iloc[:, -1].values然后我们应该分为 train 和 test 集。
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42, shuffle=True)
x_train.shape, y_train.shape, x_test.shape, y_test.shape
# ((37, 3), (37,), (10, 3), (10,))7.1 Model
from sklearn.linear_model import LinearRegression
# create model
model = LinearRegression()7.2 训练
model.fit(x_train, y_train)model.intercept_, model.coef_7.3 测试
# Test model score for train data
model.score(x_train, y_train)
# 0.966
# Test model score for test data
model.score(x_test, y_test)
# 0.91# Test model score for test data
model.score(x_test, y_test)
# 0.917.4 预测
y_hat = model.predict(x_test[[0], :])
y_hat
# array([103132.59393452])八、结论
在 第 4 部分 中,我们讨论了多元线性回归以及我们应该如何预处理数据。在第 5 部分:非线性回归,我们讨论了非线性回归是一种回归分析形式,其中观察数据由函数建模,该函数是模型参数的非线性组合,并取决于一个或多个自变量。