VCNet论文阅读笔记
0、基本信息
| 信息 | 细节 |
|---|---|
| 英文题目 | VCNet and Functional Targeted Regularization For Learning Causal Effects of Continuous Treatments |
| 翻译 | VCNet和功能目标正则化用于学习连续处理的因果效应 |
| 单位 | 芝加哥大学 |
| 年份 | 2021 |
| 论文链接 | [2103.07861] VCNet和功能定向正则化用于学习连续处理的因果效应 (arxiv.org) |
| 代码链接 | https://github.com/lushleaf/varying-coefficient-net-with-functional-tr |
| 发表会议 | ICLR 2021 Conference Program Chairs |
1、摘要
背景:因果推断(casual inference)在智能营销、药物治疗、决策上有广泛的应用,比如优惠券对用户购买意愿的影响、药品多大程度改善或治愈疾病、某项政策提高多少就业率等。(即,预估一种干预因素(treatment)对结果(outcome)的影响(treatment effect)),本文的目标问题就是获得ADRF曲线(平均剂量反应曲线):x轴是药物浓度(treatment),y轴是患者效果(outcome)。
存在问题:
-
大多数uplift相关的论文都是关于binary treatment的因果效应估计,然而现实生活中,我们却经常遇到连续treatment (continues treatment)的情况。比如电商发放优惠券的满减金额是连续的,医生给病人开药的剂量是连续。那么我们应该如何对continues treatment对情况进行因果效应估计呢?
-
以前解决连续treatment的方法是将连续treatment分成多个blocks,使用不同的head处理不同的block,但是这样获得的outcome是不连续的(对应下图的Drnet曲线)。
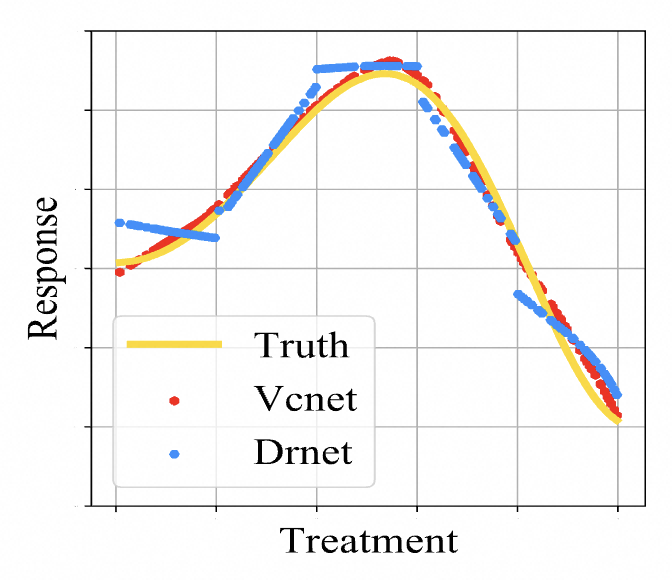
- 神经网络处理这个问题大多是,神经网络第一层是 ( t , x ) (t,x) (t,x),最后一层是 y y y,这样做会存在treatment可能会在高维度表征中丢失的问题,以前的处理方法是将 t t t,加到每个隐藏层上,但是这样做让预测更加的不连续。
文章贡献:
-
提出一个可变系数神经网络VCNet能处理连续干预的网络结构
-
推广了目标正则化,以获得整个ADRF曲线的双重鲁棒估计。
2、问题陈述和建模
iid 样本 { ( y _ i , x _ i , t _ i ) } _ i = 1 n \{(y\_i,\boldsymbol{x}\_i,t\_i)\}\_{i=1}^n {(y_i,x_i,t_i)}_i=1n,其中X是协变量向量,T是连续treatment[0,1],Y是结果
💎目标就是求平均剂量反应函数:
ψ ( t ) = E ( Y ∣ do ( T = t ) ) \psi(t)=\mathbb{E}(Y\mid\text{do}(T=t)) ψ(t)=E(Y∣do(T=t))
这里的 do 操作符表示“干预”或“人为设置”处理变量 𝑇 为 𝑡。这意味着我们要考虑的是,如果我们强制将处理设置为 𝑡,在这种情况下 𝑌的期望值。
| 患者 | 年龄 X | 治疗水平 T | 结果 Y |
|---|---|---|---|
| 1 | 30 | 0.5 | 2 |
| 2 | 30 | 0.5 | 3 |
| 3 | 50 | 0.5 | 4 |
| 4 | 80 | 0.5 | 1 |
ψ ( 0.5 ) = E ( Y ∣ do ( T = 0.5 ) ) \psi(0.5)=\mathbb{E}(Y\mid\text{do}(T=0.5)) ψ(0.5)=E(Y∣do(T=0.5))
但在实际应用中,我们通常不能直接进行干预实验,我们只能观察到变量间的关系。在观察性数据中,我们常常用条件期望来替代这个干预性期望。我们需要将这个理论性的期望转换为可实际计算的形式。
ψ ( t ) = E ( Y ∣ do ( T = t ) ) = E ( E ( Y ∣ X , T = t ) ) \psi(t)=\mathbb{E}(Y\mid\text{do}(T=t))=\mathbb{E}(\mathbb{E}(Y|X,T=t)) ψ(t)=E(Y∣do(T=t))=E(E(Y∣X,T=t))
ψ ( 0.5 ) = E ( Y ∣ do ( T = 0.5 ) ) = E ( E ( Y ∣ X , T = 0.5 ) ) \psi(0.5)=\mathbb{E}(Y\mid\text{do}(T=0.5))=\mathbb{E}(\mathbb{E}(Y|X,T=0.5)) ψ(0.5)=E(Y∣do(T=0.5))=E(E(Y∣X,T=0.5))
E ( Y ∣ 30 , T = 0.5 ) = ( 2 + 3 ) / 2 = 2.5 \mathbb{E}(Y|30,T=0.5) = (2+3)/2 = 2.5 E(Y∣30,T=0.5)=(2+3)/2=2.5
E ( Y ∣ 50 , T = 0.5 ) = 4 \mathbb{E}(Y|50,T=0.5) =4 E(Y∣50,T=0.5)=4
E ( Y ∣ 80 , T = 0.5 ) = 1 \mathbb{E}(Y|80,T=0.5) =1 E(Y∣80,T=0.5)=1
ψ ( 0.5 ) = E ( E ( Y ∣ X , T = 0.5 ) ) = E ( E ( Y ∣ 30 , T = 0.5 ) + E ( Y ∣ 50 , T = 0.5 ) + E ( Y ∣ 80 , T = 0.5 ) ) \psi(0.5)=\mathbb{E}(\mathbb{E}(Y|X,T=0.5)) = \mathbb{E}(\mathbb{E}(Y|30,T=0.5)+\mathbb{E}(Y|50,T=0.5)+\mathbb{E}(Y|80,T=0.5)) ψ(0.5)=E(E(Y∣X,T=0.5))=E(E(Y∣30,T=0.5)+E(Y∣50,T=0.5)+E(Y∣80,T=0.5))
ψ ( 0.5 ) = \psi(0.5) = ψ(0.5)= ( 2.5 + 4 + 1 ) / 3 = 2.42 (2.5+4+1)/3 = 2.42 (2.5+4+1)/3=2.42
但是这里面存在一个问题:年长的患者可能更容易在同一治疗水平下有不同的结果(X存在混杂因素)。
解决方案:
提出一个广义倾向性得分的概念
E ( E ( Y ∣ X , T = t ) ) \mathbb{E}(\mathbb{E}(Y|X,T=t)) E(E(Y∣X,T=t))需要结合所有与 𝑋 相关的信息来进行计算。然而,当你面对的是复杂的数据,有时通过所有的 𝑋 来进行估计会引入噪声或混杂因素。
使用 π ( t ∣ x ) \pi(t|x) π(t∣x)代表患者接受treatment的概率( P ( t ∣ x ) P(t|x) P(t∣x))
倾向评分提供了一种将多维数据(特征 𝑋)映射到一维(治疗概率)的方法。这一映射使得我们能够更有效地建模和学习潜在的因果关系。
ψ ( t ) = E ( Y ∣ do ( T = t ) ) = E ( E ( Y ∣ X , T = t ) ) = E ( E ( Y ∣ π ( t ∣ x ) , T = t ) ) \psi(t)=\mathbb{E}(Y\mid\text{do}(T=t))=\mathbb{E}(\mathbb{E}(Y|X,T=t)) = \mathbb{E}(\mathbb{E}(Y|\pi(t|x),T=t)) ψ(t)=E(Y∣do(T=t))=E(E(Y∣X,T=t))=E(E(Y∣π(t∣x),T=t))
π ( 0.5 ∣ 30 ) = 0.4 \pi(0.5|30) = 0.4 π(0.5∣30)=0.4
π ( 0.5 ∣ 50 ) = 0.3 \pi(0.5|50) = 0.3 π(0.5∣50)=0.3
π ( 0.5 ∣ 80 ) = 0.3 \pi(0.5|80) = 0.3 π(0.5∣80)=0.3
ψ ( 0.5 ) = E ( E ( Y ∣ π ( t ∣ x ) , T = t ) ) = ( 2.5 ∗ 0.4 + 4 ∗ 0.3 + 1 ∗ 0.3 ) / 1 = 2.5 \psi(0.5)= \mathbb{E}(\mathbb{E}(Y|\pi(t|x),T=t))=(2.5* 0.4+4* 0.3+1* 0.3)/1 = 2.5 ψ(0.5)=E(E(Y∣π(t∣x),T=t))=(2.5∗0.4+4∗0.3+1∗0.3)/1=2.5
通过这个过程,我们减少了由 𝑋引入的潜在偏倚,使得结果 𝑌 更好地反映了治疗的真实效果。
3、VCNet模型原理
3.1 基本结构
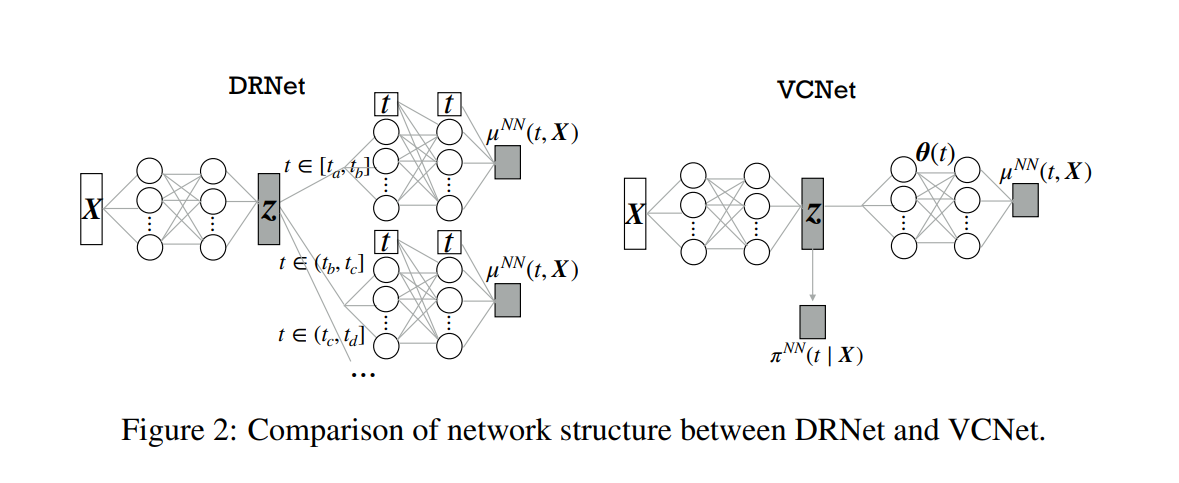
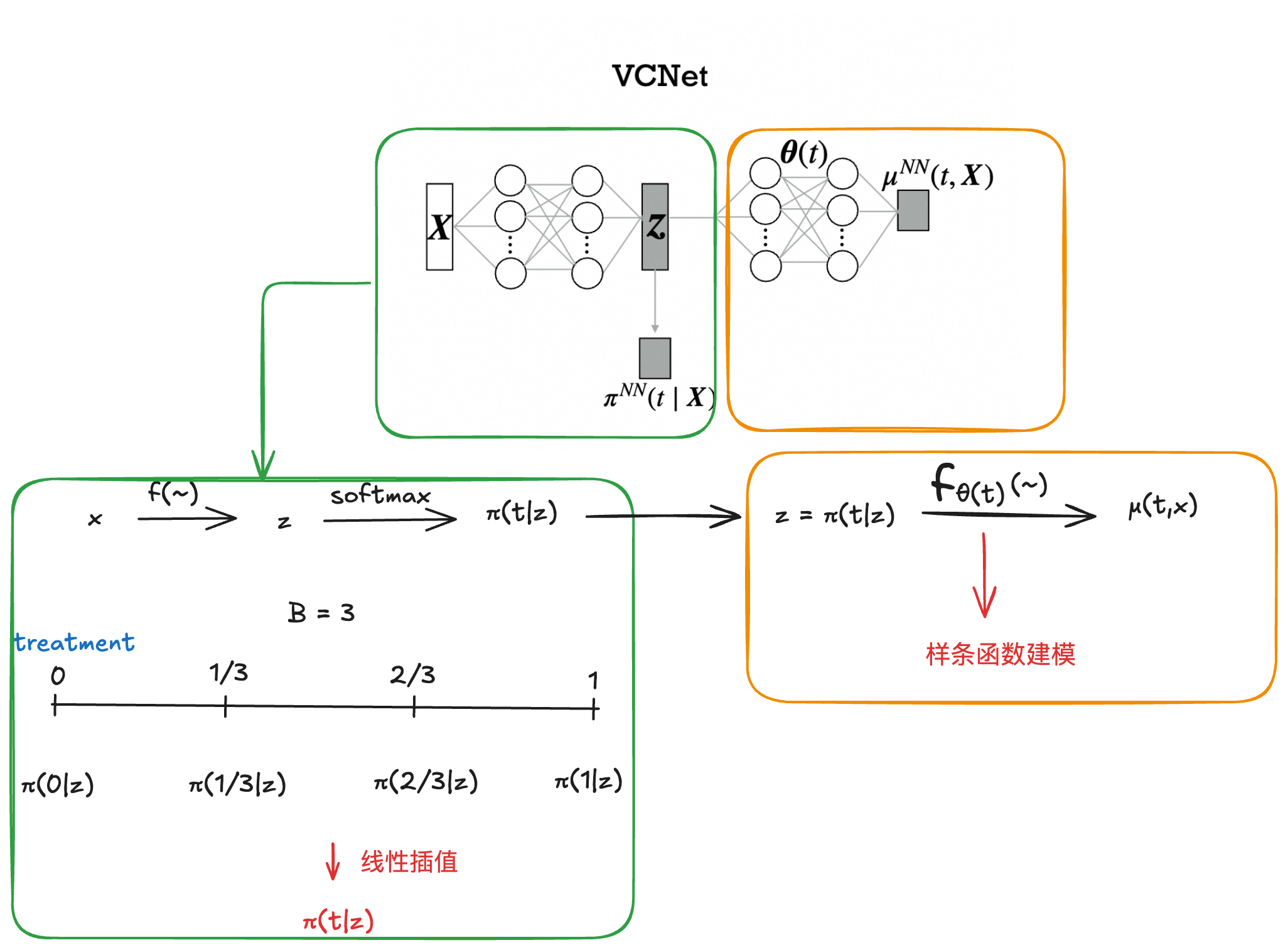
先使用简单的神经网络估计 π ( t ∣ x ) \pi(t|x) π(t∣x),之后使用VCNet得到预测结果
3.1 𝜋(𝑡|𝑋)估计
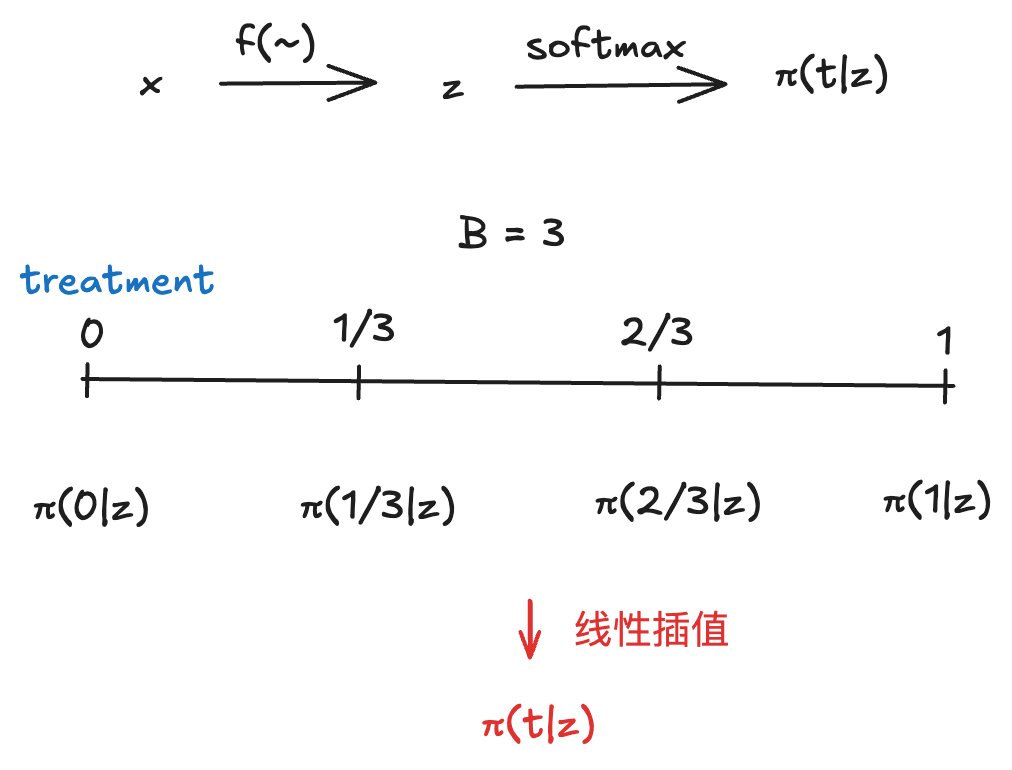
由于本文所提到的treatment是连续的,因此本文将treatment分成了B个grid区间,通过softmax转化成一个多分类问题,再通过差值估计得到最后的估计结果。
π _ g r i d N N ( x ) = s o f t m a x ( w z ) \pi\_{grid}^{NN}(x)=softmax(wz) π_gridNN(x)=softmax(wz)
π N N ( t ∣ x ) = π _ g r i d t _ 1 , N N ( x ) + B ( π _ g r i d t _ 2 , N N ( x ) − π _ g r i d t _ 1 , N N ( x ) ) ( t − t _ 1 ) \\\pi^{NN}(t|x)=\pi\_{grid}^{t\_1,NN}(x)+B(\pi\_{grid}^{t\_2,NN}(x)-\pi\_{grid}^{t\_1,NN}(x))(t-t\_1) πNN(t∣x)=π_gridt_1,NN(x)+B(π_gridt_2,NN(x)−π_gridt_1,NN(x))(t−t_1)
3.2 VCNet变系数估计
那如何得到变系数?VCNet中采用样条估计得到 𝜃(𝑡),样条通过对间断点处的导数进行约束,可以实现间断点处的连续性。
一些简单的数学知识可以参考:码农小哥:一文读懂三次样条、曲线连续
假设 θ _ i ( t ) = ∑ _ l = 1 L a _ i , l ϕ _ l N N ( t ) \theta\_i(t)=\sum\_{l=1}^La\_{i,l}\phi\_l^{NN}(t) θ_i(t)=∑_l=1La_i,lϕ_lNN(t)KaTeX parse error: Undefined control sequence: \[ at position 11: \theta(t)=\̲[̲\theta\_{1}(t),…, 𝑑𝜃(𝑡) 是 𝜃(𝑡) 的维度。
则
其中, { ϕ _ l N N ( t ) } _ l = 1 L \left\{\phi\_{l}^{NN}(t)\right\}\_{l=1}^{L} {ϕ_lNN(t)}_l=1L为样条基, 𝑎𝑖,𝑙 为系数。则我们有
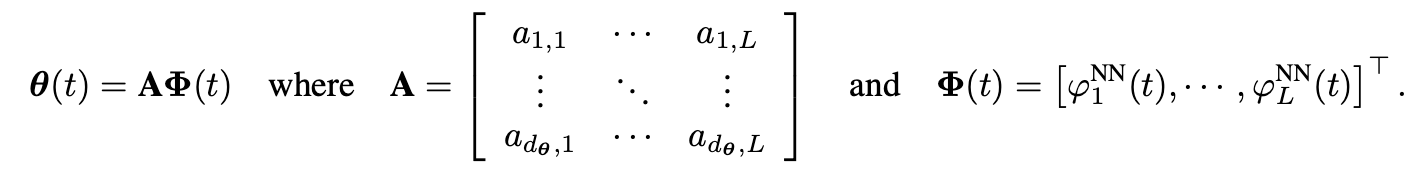
这里样条基的形式可以任意选择,假设以DRNet的多头形式估计变系数,DRNet其实也是VCNet的一个特例。
3.3 损失函数
同时优化π和μ
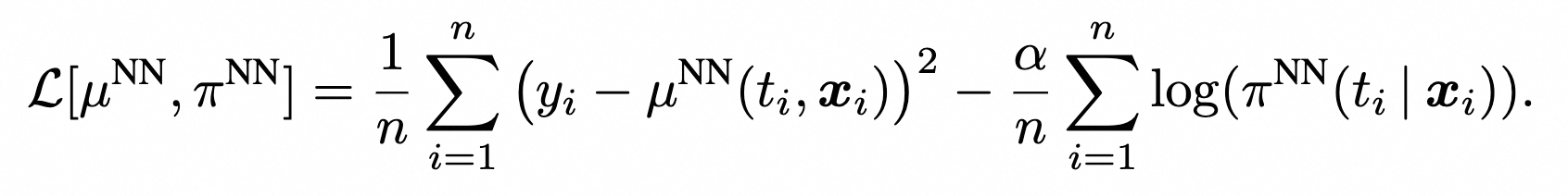
得到最优解
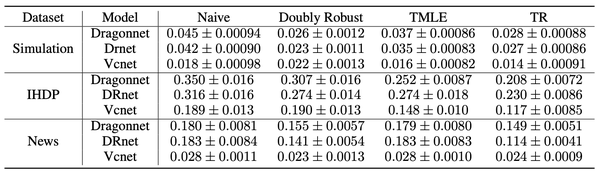
4、结果
从论文实验效果上看,VCNet对连续treatment的估计效果确实挺好的,同时加上DR也能很好的提升效果。

参考
-
连续干预下的深度因果推断 – VCNet解读 - 知乎 (zhihu.com)
-
因果推断笔记 | 连续型treatment因果效应估计之DRNet&VCNet - 知乎 (zhihu.com)
















![World of Warcraft [CLASSIC] International translation bug](https://i-blog.csdnimg.cn/direct/a04cea3d10f040db9bb155618147dca0.jpeg)

