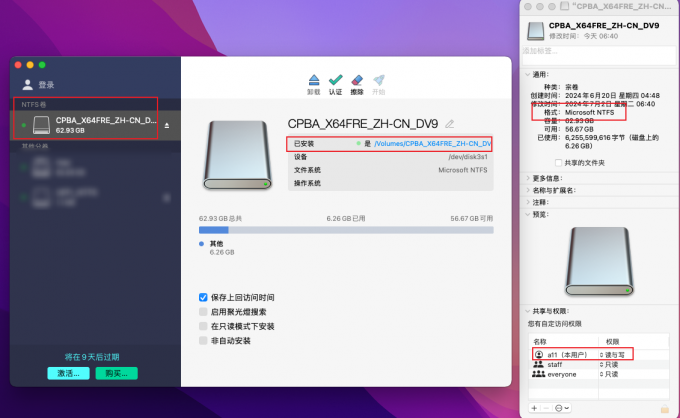
题目描述

思路
快慢指针
结论
我们需要用到一个重要的结论:让一个指针从链表起始位置开始遍历链表,同时让一个指针从判环时相遇点的位置开始绕环运行,两个指针都是每次均走一步,最终肯定会在入口点的位置相遇。
画图解释
1.利用快慢指针找到相遇点

2. 定义两个指针,pcur从链表的起始位置开始遍历,slow(fast)从相遇点开始遍历,pcur和slow均走一步,两个指针相遇的位置是入口点。

证明结论
是不是觉得上面的过程是个巧合?那我们来证明一下!

说明: H为链表的起始点,E为环入口点,M是判环时候相遇点
设:
环的长度为R,H到E的距离为L,E到M的距离为 X ,则:M到E的距离为R-X
在判环时,快慢指针相遇时所走的路径的长度:
fast:L+X+nR
slow: L+R
注意:
1.当慢指针进入环时,快指针可能已经在环中绕了n圈了,n至少为1。
因为:快指针先进环走到M的位置,,最后又在M的位置与慢指针相遇。
2.慢指针进环之后,快指针肯定会在慢指针走一圈之内追上慢指针
因为:慢指针进环后,快慢指针之间的距离最多就是环的长度,而两个指针在移动时,每次它们至今
的距离都缩减一步,因此在慢指针移动一圈之前快指针肯定是可以追上慢指针的,而快指针速度是慢
指针的两倍,因此有如下关系是:
2*(L+X)=L+X+nR
LX=nR
L=nR-X
L=(n-1)R+(R-X)
(n为1,2,3,4......,n的大小取决于环的大小,环越小n越大)
极端情况下,假设n=1,此时:L=R-X
即:一个指针从链表起始位置运行,一个指针从相遇点位置绕环,每次都走一步,两个指针最终会在入口点的位置相遇
完整代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head)
{
ListNode*slow=head;
ListNode*fast=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
//相遇
ListNode*pcur=head;
while(pcur&&slow)
{
if(pcur==slow)
{
return pcur;
}
pcur=pcur->next;
slow=slow->next;
}
}
}
//说明链表不带环
return NULL;
}