纯跟踪算法(Pure Pursuit Algorithm)是一种用于路径跟踪的几何控制算法,广泛应用于自动驾驶、机器人导航等领域。其基本思想是通过选择预定路径上的目标点(预瞄点),并控制转向角,使车辆不断逼近并跟随该目标点,从而达到路径跟踪的效果。
1. 纯跟踪算法的基本原理
在纯跟踪算法中,控制车辆的转向角是通过“追逐”路径上的一个预瞄点来实现的。该预瞄点通常位于车辆前方一定距离处。算法将车辆看作一个简单的自行车模型,并通过几何方法计算车辆需要的转向角,使得车辆沿着路径前进。
1.1 自行车模型
纯跟踪算法常采用自行车模型来简化车辆的运动学行为。该模型假设车辆的后轮作为参考点(简化车辆为一条直线),并且前轮负责控制转向。模型中车辆的运动主要由以下几个变量决定:
:车辆的轴距(前后轮之间的距离)
:车辆的速度
:车辆的转向角
:车辆当前的位置
:车辆当前的朝向角,即车头的方向
1.2 预瞄点
预瞄点是预定义路径上的一个点,通常位于车辆前方一段距离处,距离为,称为预瞄距离(Lookahead Distance)。预瞄距离
是算法的一个重要参数,选择合适的预瞄距离对于跟踪精度和系统稳定性至关重要。
2. 纯跟踪算法的核心几何推导
2.1 预瞄距离计算
假设车辆的当前位置为,朝向角为
,预瞄点的坐标为
,则预瞄点与车辆之间的欧几里得距离(预瞄距离)为:
预瞄距离可以是一个固定值,也可以随着车辆速度变化动态调整,通常速度越高,预瞄距离越大。
2.2 目标角度 的计算
的计算
偏航角是车辆当前朝向与车辆到目标点之间连线的夹角。它定义为:
这个角度反映了车辆当前的行驶方向与目标点方向的偏差。它是生成转向指令的基础。
2.3 轨迹曲率与转向角的关系
根据几何关系,车辆到预瞄点的距离为,目标偏航角为
,通过几何推导可以得到转向角
与这些量的关系。具体地,假设车辆的转向角能够控制其沿着圆形轨迹行驶,则车辆沿圆弧行驶的曲率
与转向角
的关系为:
由于转向角与车辆曲率之间的关系为:
代入上式,可以得到转向角的最终表达式:
其中,为车辆的轴距,
是车辆的偏航角,
是预瞄距离。
3. 纯跟踪算法的实现步骤
-
确定预瞄点:在车辆当前位置沿着预定路径向前寻找距离
处的目标点
。这一点是车辆在接下来的控制周期内要追逐的目标。
-
计算偏航角
:根据车辆当前的朝向角
和预瞄点的位置,计算车辆与目标点之间的偏航角
。
-
计算转向角
:根据偏航角
、车辆轴距
和预瞄距离
,使用上述公式计算车辆的转向角
。
-
执行控制:根据计算得到的转向角
,调整车辆的方向,使其逐步逼近并跟随预定路径。
-
更新车辆位置:在每个控制周期内,根据车辆的速度和转向角,更新车辆的当前位置和朝向角,然后重复以上步骤,直到车辆完成路径跟踪。
4. 应用场景与优化
4.1 应用场景
- 自动驾驶车辆:纯跟踪算法常用于自动驾驶车辆的路径跟踪,尤其是在低速和中速的情况下,例如泊车、低速路径跟踪。
- 物流机器人:在工业和仓储场景中,物流机器人通常使用纯跟踪算法沿着预定路径移动。
- 无人机导航:无人机在进行平面路径规划时也可以采用纯跟踪算法,使得无人机能够沿着预设轨迹飞行。
4.2 优化
-
动态调整预瞄距离:预瞄距离
可以与车辆速度成比例,速度越大,预瞄距离也应该增大,以保持路径跟踪的平滑性和稳定性。
-
与其他控制算法结合:在更复杂的场景中,纯跟踪算法可以与更先进的控制算法结合,例如模型预测控制(MPC)和线性二次调节器(LQR),提高系统的鲁棒性和性能。
5. 优缺点
优点
- 简单易实现:纯跟踪算法基于简单的几何关系,计算复杂度低,适合实时应用。
- 响应平滑:在低速或路径平缓的情况下,纯跟踪算法能够生成平滑的转向指令,保证车辆平稳行驶。
缺点
- 精度有限:当车辆速度较高或路径曲率变化较大时,纯跟踪算法的跟踪精度可能下降,容易产生跟踪误差。
- 忽略动态特性:纯跟踪算法未考虑车辆的动态特性(如车轮打滑、惯性等),因此在某些极端情况下,可能无法准确跟踪预定路径。
6、代码示例
import numpy as np
import math
import matplotlib.pyplot as plt
from matplotlib.animation import PillowWriter
import imageio
# 车辆模型
class Vehicle:
def __init__(self, x=0.0, y=0.0, theta=0.0, speed=0.0, L=2.9):
"""
初始化车辆模型
x, y: 初始位置
theta: 初始航向角
speed: 初始速度
L: 车辆轴距
"""
self.x = x
self.y = y
self.theta = theta
self.speed = speed
self.L = L
self.max_speed = 3.0 # 车辆最大速度
def update(self, delta, acceleration, dt):
"""
更新车辆状态
delta: 转向角
acceleration: 加速度
dt: 时间步长
"""
self.speed += acceleration * dt
self.speed = min(self.speed, self.max_speed) # 限制车辆速度
self.x += self.speed * math.cos(self.theta) * dt
self.y += self.speed * math.sin(self.theta) * dt
self.theta += self.speed / self.L * math.tan(delta) * dt
# Pure Pursuit控制器
class PurePursuitController:
def __init__(self, k=0.1, max_lookahead=30.0, min_lookahead=5.0, L=2.9):
"""
初始化Pure Pursuit控制器
k: 速度比例因子,用于计算lookahead距离
max_lookahead: 最大lookahead距离
min_lookahead: 最小lookahead距离
L: 车辆轴距
"""
self.k = k
self.max_lookahead = max_lookahead
self.min_lookahead = min_lookahead
self.L = L
def calc_lookahead_distance(self, speed):
"""
根据速度计算lookahead距离
speed: 当前车辆速度
"""
lookahead_distance = self.k * speed
return max(self.min_lookahead, min(lookahead_distance, self.max_lookahead))
def pure_pursuit_control(self, vehicle, cx, cy):
"""
计算Pure Pursuit控制下的转向角
vehicle: 当前车辆状态
cx, cy: 参考轨迹的x, y坐标
"""
lookahead_distance = self.calc_lookahead_distance(vehicle.speed)
# 寻找离车辆最近的轨迹点
closest_idx = -1
closest_dist = float("inf")
for i in range(len(cx)):
dist = self.calc_distance(cx[i], cy[i], vehicle.x, vehicle.y)
if dist < closest_dist:
closest_idx = i
closest_dist = dist
# 根据lookahead距离找到目标点
target_idx = closest_idx
for i in range(closest_idx, len(cx)):
dist = self.calc_distance(cx[i], cy[i], vehicle.x, vehicle.y)
if dist >= lookahead_distance:
target_idx = i
break
# 计算目标点的转向角
target_x = cx[target_idx]
target_y = cy[target_idx]
alpha = math.atan2(target_y - vehicle.y, target_x - vehicle.x) - vehicle.theta
delta = math.atan2(2 * self.L * math.sin(alpha), lookahead_distance)
return delta, target_idx
@staticmethod
def calc_distance(px, py, x, y):
"""计算两点间的欧氏距离"""
return np.sqrt((px - x) ** 2 + (py - y) ** 2)
# PID速度控制器
class PIDController:
def __init__(self, Kp, Ki, Kd, target_speed):
"""
初始化PID控制器
Kp, Ki, Kd: PID控制参数
target_speed: 目标速度
"""
self.Kp = Kp
self.Ki = Ki
self.Kd = Kd
self.target_speed = target_speed
self.integral = 0
self.previous_error = 0
def control(self, current_speed, dt):
"""
计算速度控制下的加速度
current_speed: 当前速度
dt: 时间步长
"""
error = self.target_speed - current_speed
self.integral += error * dt
derivative = (error - self.previous_error) / dt
self.previous_error = error
acceleration = self.Kp * error + self.Ki * self.integral + self.Kd * derivative
return acceleration
def update_target_speed(self, distance_to_goal, stop_threshold=3.0):
"""
根据目标距离更新目标速度(用于平滑停止)
distance_to_goal: 车辆距离终点的距离
stop_threshold: 停止距离的阈值
"""
if distance_to_goal < stop_threshold:
self.target_speed = 0.0 # 当接近终点时,目标速度设为0
# 轨迹
class Trajectory:
def __init__(self):
"""
初始化参考轨迹
"""
self.cx = np.arange(0, 50, 0.5)
self.cy = [math.sin(ix / 5.0) * ix / 2.0 for ix in self.cx]
def get_trajectory(self):
"""获取轨迹的x, y坐标"""
return self.cx, self.cy
# 主函数
def main():
vehicle = Vehicle(x=0.0, y=0.0, theta=0.0, speed=0.0, L=2.9)
controller = PurePursuitController(k=0.1, max_lookahead=30.0, min_lookahead=1.5, L=2.9)
trajectory = Trajectory()
cx, cy = trajectory.get_trajectory()
pid_controller = PIDController(Kp=1.0, Ki=0.1, Kd=0.01, target_speed=3.0)
dt = 0.1
x_history = []
y_history = []
# 创建图形
fig, ax = plt.subplots()
# GIF帧列表
frames = []
for t in range(500):
# 计算车辆到终点的距离
distance_to_goal = controller.calc_distance(cx[-1], cy[-1], vehicle.x, vehicle.y)
pid_controller.update_target_speed(distance_to_goal, stop_threshold=3.0)
# 计算车辆的转向角度并更新车辆位置
delta, target_idx = controller.pure_pursuit_control(vehicle, cx, cy)
acceleration = pid_controller.control(vehicle.speed, dt)
vehicle.update(delta, acceleration, dt)
# 保存车辆运动轨迹
x_history.append(vehicle.x)
y_history.append(vehicle.y)
# 每2步更新一次图形,提升性能
if t % 2 == 0:
ax.cla()
ax.plot(cx, cy, "-r", label="reference trajectory")
ax.plot(x_history, y_history, "-b", label="vehicle trajectory")
ax.plot(cx[target_idx], cy[target_idx], "go", label="lookahead point")
ax.set_xlim(0, 50)
ax.set_ylim(-20, 25)
ax.set_title(f"Pure Pursuit with PID - Step {t}")
ax.set_xlabel("x [m]")
ax.set_ylabel("y [m]")
ax.grid(True)
# 渲染当前帧
fig.canvas.draw()
# 将当前帧保存到 GIF 帧列表
image = np.frombuffer(fig.canvas.tostring_rgb(), dtype='uint8').reshape(fig.canvas.get_width_height()[::-1] + (3,))
frames.append(image)
# 实时显示
plt.pause(0.01)
# 到达终点并停止
if distance_to_goal < 0.5:
print("Reached the goal!")
break
# 保存为GIF
gif_filename = 'pure_pursuit_simulation.gif'
imageio.mimsave(gif_filename, frames, fps=10)
print(f"Simulation saved as {gif_filename}")
if __name__ == '__main__':
main()
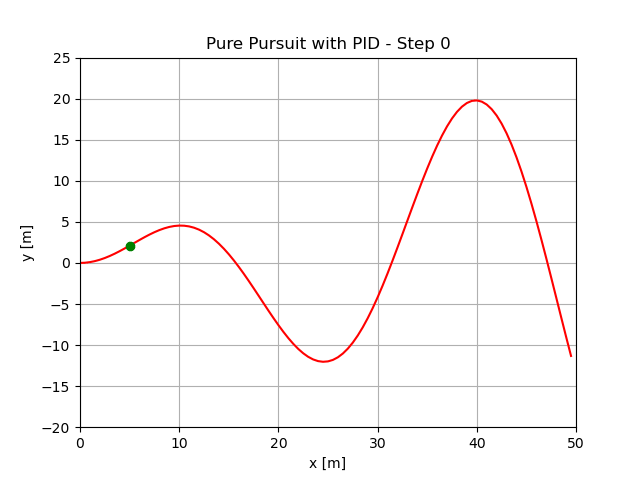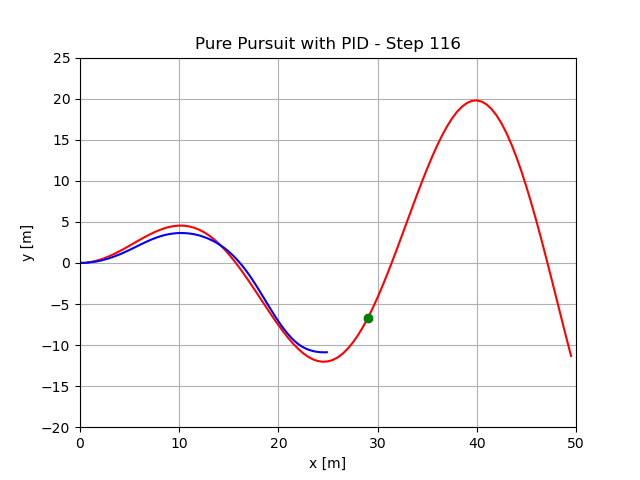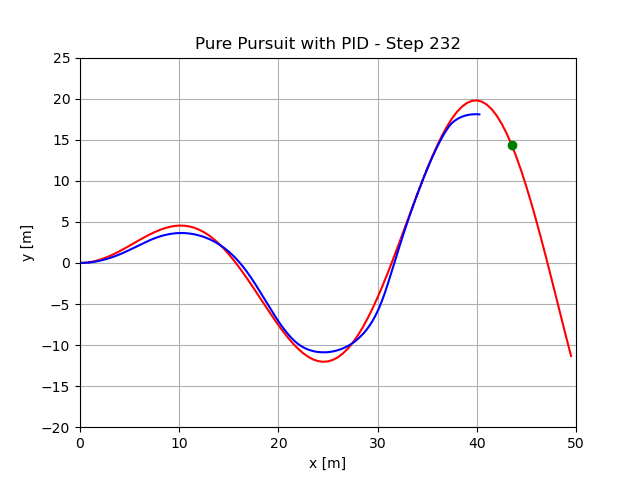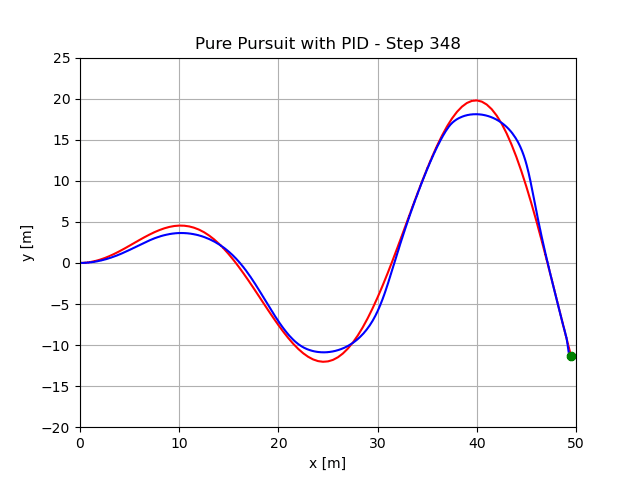
最小预瞄距离1.5m,执行结果:
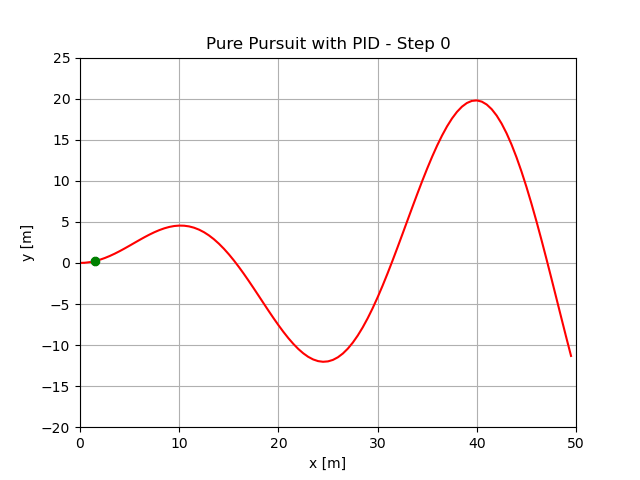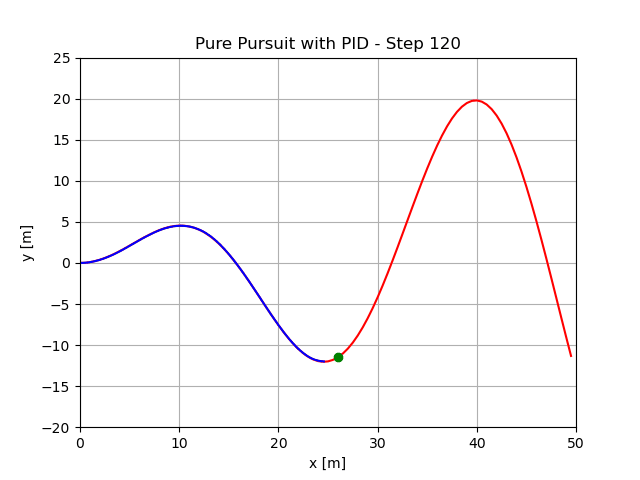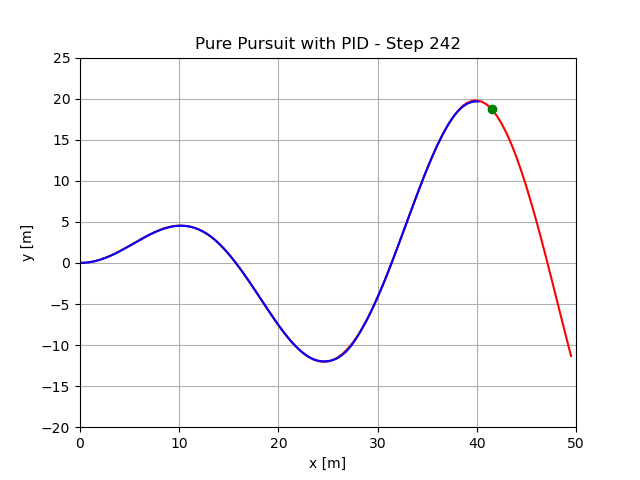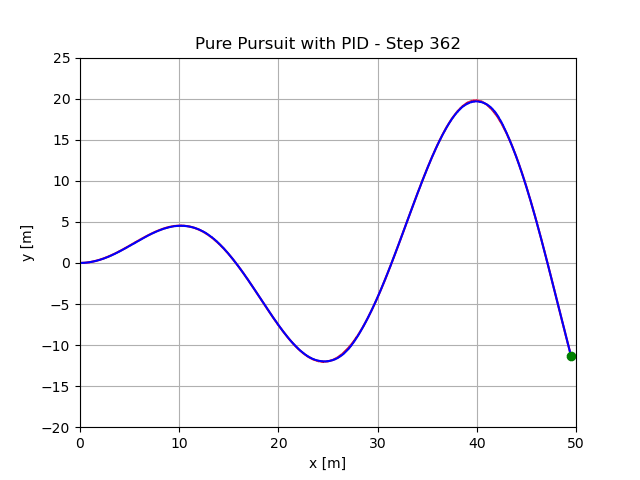
最小预瞄距离5m,执行结果:
7. 讨论
在纯跟踪(Pure Pursuit, PP)算法中,前视距离(也称为预瞄距离)是一个关键参数,它直接影响到车辆的驾驶性能和路径跟踪的准确性。前视距离是指从车辆当前位置到目标点的距离。这个距离的设置会根据车辆的速度和动态条件进行调整。以下是预瞄距离远近对车辆控制的主要影响:
预瞄距离过长
稳定性增加:较长的预瞄距离可以使车辆更加稳定,特别是在高速行驶时。车辆对即时路况的反应会有所延迟,从而在一定程度上减小因路面突变导致的影响。
减小转向敏感性:随着预瞄距离的增加,车辆对转向的响应会变得不那么敏感,这意味着转向动作更加平缓,对于保持高速行驶的车辆稳定性是有利的。
跟踪误差可能增加:在弯道或复杂路段,长预瞄距离可能导致车辆无法及时调整行驶路径以精确跟踪路线,尤其是在紧急转弯或连续弯道的情况下。
预瞄距离过短
提高转向敏感性:较短的预瞄距离使得车辆对转向输入更加敏感,这有助于在技术性较高的低速路段(如城市环境或障碍物较多的路段)中快速调整方向。
稳定性减小:在高速行驶时,较短的预瞄距离可能会导致车辆稳定性下降,因为车辆需要频繁并且剧烈地调整转向来维持路径,这可能会引起车辆摇摆或其他不稳定行为。
减少跟踪误差:在复杂或紧急转弯情况下,短预瞄距离有助于车辆更精确地跟踪路径,因为车辆可以更快地响应路线上的变化。















![24-9-17-读书笔记(十八)-《契诃夫文集》(二)上([俄] 契诃夫 [译] 汝龙 )](https://i-blog.csdnimg.cn/direct/119d4e8f7a1440d7a0fa84ddbf230581.png)

