题目截图

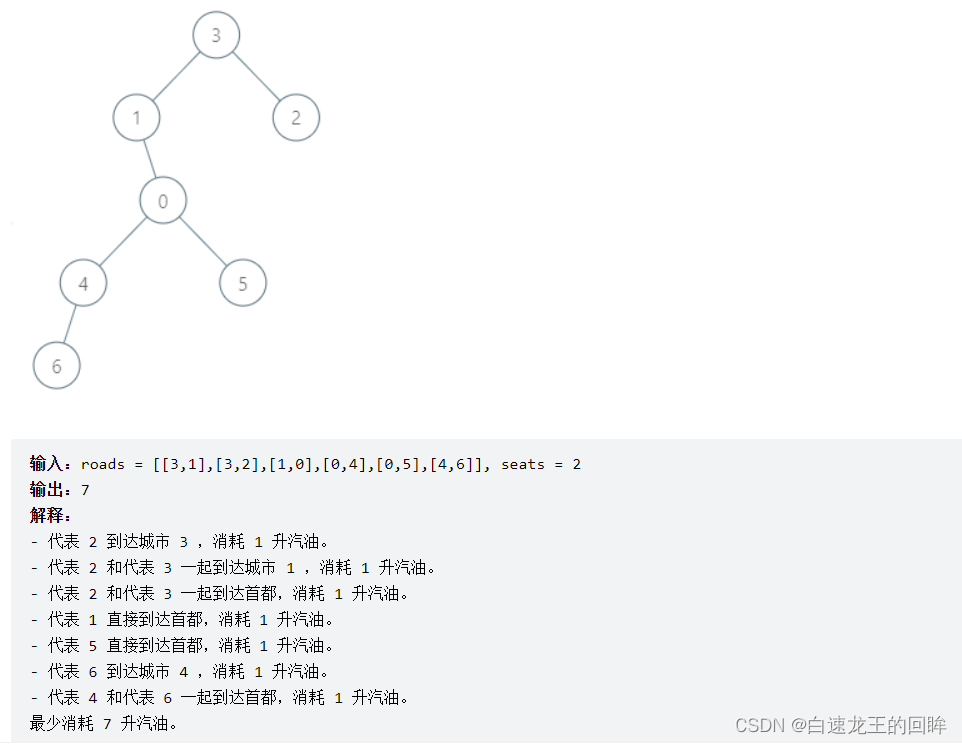
题目分析

• 0作为root
• 从边的角度出发
• 每个点都向0的方向聚集
• 比如大家已经由四面八方聚集到了x，x的fa固定的，假设为y
• 那么x到y要多少辆车？
• 设size（x）为x子树大小
• x到y需要ceil（x / seats)量车
• 每条边都需要计算一次这个数，累加到ans
• 特别地，0没有fa节点，不用考虑
• 也就是说，为了往0聚集，每条边都要承受一定的压力，这个压力需要由多少辆车来缓解？
• 从叶子往root，边的压力是需要累加的，因为要一直走到root节点截止
• 思路变为求解每个子树的大小，同时看看往上每条边的压力需要多少辆车来缓解

ac code

class Solution:
    def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
        # 考虑每条边最少需要多少车
        # 向上取整
        # 考虑子树大小，向上的流量就是子树的大小
        ans = 0
        g = defaultdict(list)
        for x, y in roads:
            g[x].append(y)
            g[y].append(x)
        
        def dfs(x, fa): # 返回的是子树的size
            size = 1
            for child in g[x]:
                if child != fa:
                    size += dfs(child, x)
            if x: # 不统计root
                nonlocal ans
                ans += (size + seats - 1) // seats # size / seats 向上取整
            return size
        
        dfs(0, -1)
        return ans

总结

• 我图论有点lj
• 思维转换到子树大小统计
• 怎么想到的？因为大家都往root靠拢，首先会聚集到一个lca，对于lca来说就是就是求子树大小了
• 为什么要求子树大小？因为要往fa靠，下面的压力会聚集到这条边上，这就不得不求压力是多少？也就是子树大小了，完美。。。