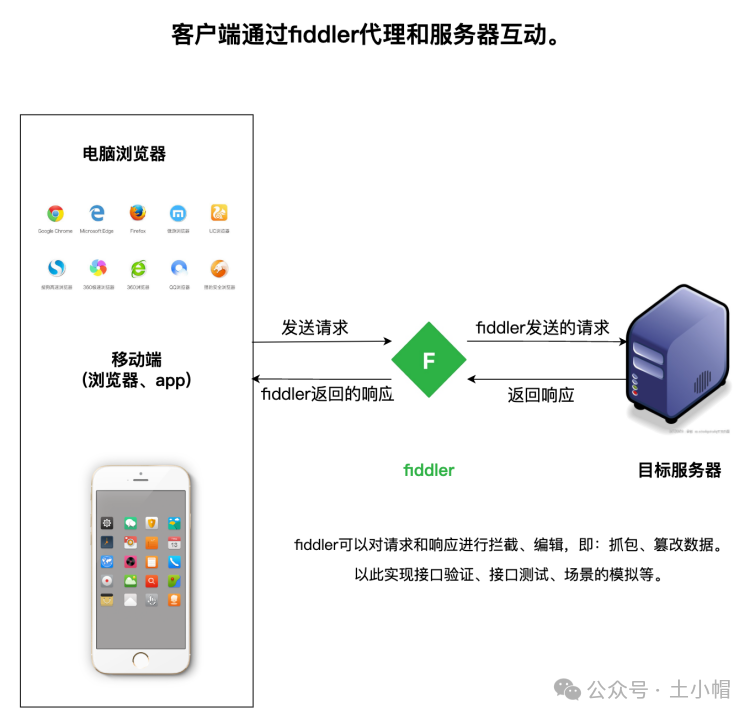
以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

思路

区间排序：

开始位置  ——> 升序排序，若多个开始位置相同，按照结束位置降序排序

——> 相同开始位置的多个区间中，第一个区间为最长区间，仅保留最长区间

使用列表mergedList存储合并后的区间(无法事先知道合并后剩余多少区间)。

遍历排序后的数组intervals，首先将首个区间(即intervals[0])添加到列表中，然后对其余的区间依次判断是否需要和已有区间合并，并更新列表。

对于遍历到的每个区间，判断与intervals中的上一个区间开始位置是否相同，相同则跳过；不相同时，将当前区间记为curr，将列表中最后一个区间记为prev。比较curr的开始位置和prev的结束位置。

• 如果curr[0] <= prev[1]  =》左端点小于右端点，（此时curr[0] > prev[0]，curr[1] > prev[1]）则prev和curr重叠，需要合并
  开始位置：prev[0]；结束位置：max(prev[1[, curr[1])。
  更新prev[1]的值，不需要将curr添加到列表中；
  prev[0]        curr[0]        prev[1]        curr[1]
• 如果curr[0] > prev[1]，则curr与prev不重叠，将curr添加到列表中。
  prev[0]        prev[1]        curr[0]       curr[1]

public class Solution {
    public int[][] Merge(int[][] intervals) {
        Array.Sort(intervals, (a, b) =>
        {
            if(a[0] != b[0])
                return a[0] - b[0];//a[0]与b[0]升序排序
            else
                return b[1] - a[1];//b[1]与a[1]降序排序
        });

        List<int[]> mergedList = new List<int[]>();
        mergedList.Add(intervals[0]);
        for(int i = 1; i < intervals.Length; i++)
        {
            int[] curr = intervals[i];
            int[] prev = mergedList[mergedList.Count - 1];
            if(curr[0] == prev[0])
                continue;
            if(curr[0] <= prev[1])
                prev[1] = Math.Max(prev[1], curr[1]);
            else
                mergedList.Add(curr);
        }
        return mergedList.ToArray();
    }
}

复杂度分析

• 时间复杂度：O(nlogn)，其中 n 是数组 intervals 的长度。时间复杂度：O(nlogn)，其中 n 是数组 intervals 的长度。

• 空间复杂度：O(n)，其中 n 是数组 intervals 的长度。存储合并后的区间的列表需要 O(n) 的空间。