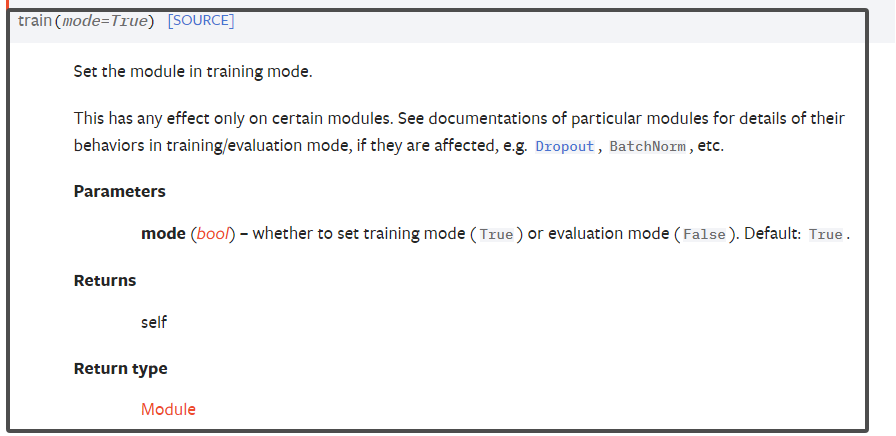
MFEA/D-DRA–基于分解和动态资源分配的多目标多任务优化

title： A Multiobjective multifactorial optimization algorithm based on decomposition and dynamic resource allocation strategy

author： Shuangshuang Yao, Zhiming Dong, Xianpeng Wangc, Lei Ren.

journal： Information Sciences (ins)

DOI：https://doi.org/10.1016/j.ins.2019.09.058

code:

1.主要贡献：

​ 1）提出了MFEA/D-DRA，它可以根据不同任务的难易程度自动地分配合理的计算资源；

​ 2）提出了一种多目标多任务优化问题的分解策略，它将每个多目标优化问题都分解为一组单目标优化子问题，并在统一搜索空间中同时求解所有的这些单目标子问题。

​ 3）提出了一种多因子环境下的动态资源分配策略来求解这些单目标优化问题。

2.问题提出：

​ 为了解决MO-MFO问题，除了探索和利用不同任务之间的有用信息来加速优化外，在不同的任务之间合理分配计算资源也很重要，因为不同的任务往往会有不同的难易程度。

3.MFEA/D-DRA：

3.1 MFEA/D-DRA的算法框架

​ 1）与传统的MOEA/D不同，MFEA/D-DRA为每个mop问题都设置了一组权重向量；

​ 2）MFEA/D-DRA使用rmp来控制不同任务间的信息交互；

​ 3）MFEA/D-DRA的子代更新策略：当子代个体的父代个体拥有不同的技能因子，该子代只会与具有相同技能因子的父代进行更新。

​ 4）适应度也可以看作是个体在种群中的竞争力，适应度值越大，则该个体更有竞争力，需要投入更多资源。并且个体的适应度值是动态更新的。

## 3.2 初始化

​ 在初始化阶段，每个MOP任务都被分解为一组单目标子问题。其中，对于一个任务${\tau }_{mop}^k$， Λ k = { w 1 , w 2 , . . . , w N k } , N k = N / K \Lambda_k=\{w_1,w_2,...,w_{N_k}\},N_k=N/K Λk​={w1​,w2​,...,wNk​​},Nk​=N/K是权重向量，$P_k=p_1^k,p_2^k,...,p_{N_k}^k$是一个子问题并且每个子问题的技能因子设置为$k$，$z_k^{\ast }$是${\tau }_{mop}^k$的理想点。

3.2 子代产生

​ 在每一代中，对于每个MOP问题，首先，通过锦标赛选择策略根据适应度值选择N/5个个体。接着，随机选择3个个体作为父代个体（如果$rand<\delta$，父代个体从邻域中选择，否则从整个$P_k$中选择）。然后，使用DE/rand/1算子和多项式突变算子产生子代。

3.3 种群更新

​ 如果$rand<rmp$，会随机选择一个其他任务，也就是说将会从不同的任务中迁移知识；

​ 替换大小$n_r$限制了需要更新的子问题的数量，防止了一个个体替换了多个个体，并可以保持种群的多样性。

3.4 适应度值更新

​ 在MO-MFEA中提到，解决MO-MFO问题的一个最大的挑战即为一个多目标优化问题（MOOP）中的候选解该如何排序，也就是说标量适应度和因子等级该如何确定。MO-MFEA使用NSGA-II的非支配排序和拥挤度距离来衡量。

​ 本文提出了一种新的适应度值计算方式：
$${\Delta }^i=\frac{g^{tch}(x_i^{old}|{\lambda }_i,z^{\ast })-g^{tch}(x_i^{new}|{\lambda }_i,z^{\ast })}{g^{tch}(x_i^{old}|{\lambda }_i,z^{\ast })}$$

$${\varphi }_i=\{\begin{array}{ll}1,& {\Delta }^i>0.001\\ (0.95+0.05\frac{{\Delta }^i}{0.001}){\varphi }_i,& otherwise\end{array}$$

4.思考

1）本文提出了两种策略来解决MO-MFO问题： 1)分解策略：MO-MFO问题转化为多组的单目标优化子问题的权重向量和比例函数，然后使用一个人口同时优化这些单目标问题；2)动态资源分配策略：在种群进化过程中，具有高适应度值的个体将获得更多的计算资源，并定期更新每个个体的标量适应量

2）本文首次研究了MTO中考虑不同任务的难易程度，并为不同的任务分配不同的计算资源。