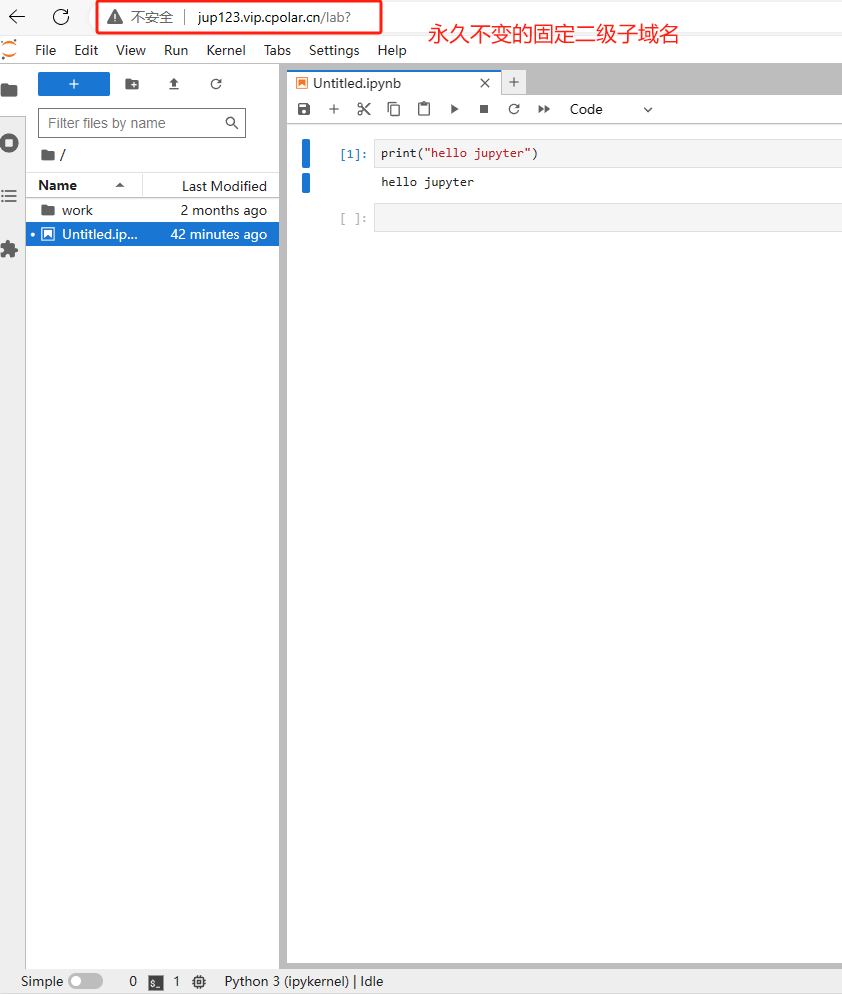
着色器通过使您能够控制渲染过程的各个方面，在图形编程中发挥着关键作用。它们在 GPU 上运行，负责操作顶点、像素和其他数据。

• 常规着色器
• 计算着色器
• 像素渲染
• 顶点着色器
• 几何体、域和外壳着色器

常规着色器

这些提示适用于所有类型的着色器。

推荐

• 避免扭曲发散常量缓冲区视图（CBV）和即时常量缓冲区（ICB）读取。
  • 当扭曲中的线程统一访问数据时，恒定缓冲区读取最有效。如果需要发散读取，请使用着色器资源视图（SRV）。
  • SRV 应优先于 CBV 的典型情况包括：
    • 骨骼或蒙皮数据
    • 查找表，如预先计算的随机数
• 要优化缓冲区和组共享内存，请使用手动位打包。在创建用于打包数据的结构时，请考虑字段可以容纳的值的范围，并选择可以包含该范围的最小数据类型。
• 通过提供预期运行时行为的提示来优化控制流。
  • 确保启用编译标志-为 DXC 绑定的所有资源（或 D3DCOMPILE_all_resources_bound 在 FXC)如果可能的话。这样可以实现一组更大的驱动程序端优化。
  • 考虑在适当的情况下使用 FLATEN 和 BRANCH 关键字。
    • 条件分支可能会阻止编译器提升长延迟指令，例如纹理获取。
    • FLATTEN 关键字提示编译器可以在对语句求值之前自由地提升和启动加载操作。
• 使用根签名 1.1 指定静态数据和描述符，使驱动程序能够进行最佳着色器优化。
• 尽量减少寄存器的使用。寄存器分配可能会限制占用率，并可能迫使驱动程序将寄存器溢出到内存中。
• 加载单通道纹理四边形时，首选使用聚集指令。
  • 与由连续样本指令构建的等效操作相比，这将使预期延迟减少近 4 倍。
• 比起原始缓冲区，更喜欢结构化缓冲区。
  • 结构化缓冲区具有更严格的对齐要求，这使驱动器能够调度更高效的加载指令。
• 考虑在数学密集型着色器（例如，物理模拟和去噪器）中使用超越函数（exp、log、sin、cos、sqrt）的数值近似或预计算查找表。
• 为了在 TEX 单元中促进快速路径，最高可加速 2 倍，在某些情况下使用点过滤：
  • 点过滤已经是精确表示的低分辨率纹理。
  • 正在以其本机分辨率访问的纹理。

不推荐

• 不要认为半精度浮点运算总是比全精度浮点运算快，反之亦然。
  • 在 NVIDIA Ampere GPU 上，执行 FP32 和执行 FP16 指令一样高效。在精确格式之间转换的开销可能会以净损失告终。
  • NVIDIA Turing GPU 可能受益于使用 FP16 数学，因为 FP16 的发布速率是 FP32 的两倍。

计算着色器

计算着色器用于从数据处理和模拟到机器学习的通用计算。

推荐

• 如果可能进行跨线程通信，请考虑在组共享内存上使用 wave 内部函数。
  • Wave 内部函数不需要显式的线程同步。
  • 从 SM 6.0 开始，HLSL 本机支持 warp wide wave intrinsic，而无需使用特定于供应商的 HLSL 扩展。只有在缺少预期功能时，才考虑使用特定于供应商的 API。有关详细信息，请参阅 在 HLSL 中解锁 GPU Intrinsics。
  • 要增加原子吞吐量，请使用 wave 指令跨扭曲合并原子操作。
• 为了最大化缓存位置并提高 L1 和 L2 命中率，请尝试对全屏计算过程进行线程组 ID 刷新。
• 一个好的起点是以对应于两到八次翘曲的线组大小为目标。例如，全屏通道的线程组大小为 8x8x1 或 16x16x1。确保对着色器进行评测，并根据评测结果调整尺寸。

不推荐

• 不要使线程组的大小难以按平台和 GPU 架构进行缩放。
  • 专业化常数可以在 Vulkan 中用于在管道创建时设置维度，而 HLSL 要求在着色器编译时知道线程组大小。
• 注意线程组启动延迟。
  • 如果您的 CS 具有在大多数情况下预计会提前退出的提前退出条件，则最好选择更大的线程组维度，并减少启动的线程组总数。

像素渲染

像素着色器，也称为片段着色器，用于按像素计算效果。

推荐

• 与像素着色器中的手动深度测试相比，更喜欢使用深度边界测试或模具和深度测试。
• 深度和模板测试可能会丢弃整个 16×16 光栅瓦片，直至单个像素。确保 Early-Z 已启用。
• 注意可能迫使驾驶员禁用 Early-Z 测试的使用模式：
  • 有条件的 z 写入，如剪辑和丢弃
    • 另一种选择是考虑使用 null 混合操作
  • 像素着色器深度写入
  • 写入无人机资源
• 如果扭曲之间的延迟差异很大，请考虑将全屏过程转换为计算着色器。

不推荐

• 不要广泛使用光栅顺序视图（ROV）技术。
  • 保证订单不是免费的。
  • 始终与高级混合操作和原子学等替代方法进行比较。

顶点着色器

顶点着色器用于在逐顶点的基础上计算效果。

推荐

• 更喜欢使用压缩顶点格式。
• 与 CBV 相比，更倾向于使用 SRV 对数据进行蒙皮。这是 CBV 读数不同的典型情况。

几何体、域和外壳着色器

几何体、域和外壳着色器用于控制、评估和生成几何体，从而使镶嵌能够创建曲面和对象的动态生成。

推荐

• 使用 NVIDIA Turing 中引入的网格着色功能替换几何体、域和外壳着色器。
• 使用以下配置启用快速几何体路径：
  • 固定拓扑：扩展或减少顶点数量。
  • 固定基元类型：输入基元类型等于输出基元类型。
  • 不可变的逐顶点属性：应用程序无法更改顶点属性，只能将它们从输入复制到输出。
  • 每基元属性可变：应用程序可以为整个基元计算一个值，然后将其传递到片段着色器阶段。例如，它可以计算三角形的面积。