岭回归：带示例的分步介绍

由 AI 生成：DNA、基因组、摘要、岭回归

一、说明

岭回归是一种在独立变量高度相关的情况下估计多元回归模型系数的方法。 [ 1 ]它已用于计量经济学、化学和工程学等许多领域。[ 2 ]也称为Tikhonov 正则化，以Andrey Tikhonov命名，是一种解决不适定问题的正则化方法。[ a ]它对于缓解线性回归中的多重共线性问题特别有用，这种问题通常发生在具有大量参数的模型中。[ 3 ]通常，该方法在参数估计问题中提供了更高的效率，以换取可容忍的偏差量

二、Ridge Regression — 简短介绍

岭回归是线性回归的一种变体，专门用于解决数据集中的多重共线性问题。在线性回归中，目标是找到使观测值和预测值之间的平方差和最小化的最佳拟合超平面。但是，当存在高度相关的变量时，线性回归可能会变得不稳定并提供不可靠的估计值。

当回归模型中的两个或多个预测变量彼此中度或高度相关时，存在多重共线性。

Ridge 回归引入了一个正则化项，该项对大系数进行惩罚，有助于稳定模型并防止过度拟合。此正则化项（也称为 L2 惩罚）为优化过程添加了约束，从而影响模型为预测变量选择较小的系数。通过在很好地拟合数据和保持系数之间取得平衡，ridge 回归被证明在提高线性回归模型的稳健性和性能方面很有价值，尤其是在多重共线性的情况下。

三、线性回归 — f或良好的开端

让我们简要回顾一下线性回归是关于什么的。

在线性回归中，模型训练主要涉及查找适当的系数值。这是使用最小二乘法完成的。一个寻求使残差平方和最小化的值 β0，β1,...,βp：

3.1 Ridge Regression — 定义

岭回归与最小二乘法非常相似，不同之处在于系数是通过最小化略有不同的量来估计的。实际上，它是相同的数量，只是多了一些，我们称之为收缩惩罚。

在我们解释什么是岭回归之前，让我们先了解一下神秘的收缩惩罚是怎么回事。

3.2 收缩惩罚 — 辅助学习

岭回归中的收缩惩罚

是指添加到线性回归方程中的正则化项，以防止过拟合并解决多重共线性问题。在岭回归中，目标是最小化观测值和预测值之间的平方差之和。但是，为此添加了一个罚项，它与系数大小的平方成正比。这个惩罚项也称为 l2 范数或欧几里得范数。

λ≥0 称为该方法的 tuning 参数，单独选择。参数 λ 控制系数向 0 收缩的强度。当 λ=0 时，惩罚无效，岭回归简化为普通的最小二乘法。然而，随着 λ→∞ 惩罚的影响增加，岭回归中系数 βj 的估计值趋于零。

3.3 如何选择 λ？

如何确定使用哪个 λ 值？
你可能不喜欢这个答案。一开始，我们不得而知。
唯一的方法是测试许多值，这通常是这样做的。但是，有许多算法实现有助于选择合适的 λ，例如交叉验证。

我想强调的是，这个超参数不应该被忽视。选择正确的 λ 非常重要。

四、为什么要缩放预测变量？

还应该注意的是，收缩惩罚仅适用于系数 β1,...,βp，但不会影响截距项 β0。我们不会缩小截距 — 它表示当所有预测变量都等于 0 时对因变量平均值的预测。假设在执行岭回归之前，变量已居中为均值为零，则估计的截距将采用以下形式

应该强调的是，缩放预测变量很重要。在线性回归中，将预测变量 Xj 乘以常数 c 会使估计参数减少 1/c（意味着 Xjβj 保持不变）。但是，在岭回归中，由于收缩惩罚，缩放预测变量 Xj 可以显著改变估计参数 βj 和其他预测变量。因此，在应用岭回归之前，预测变量将被标准化为具有相同的尺度。

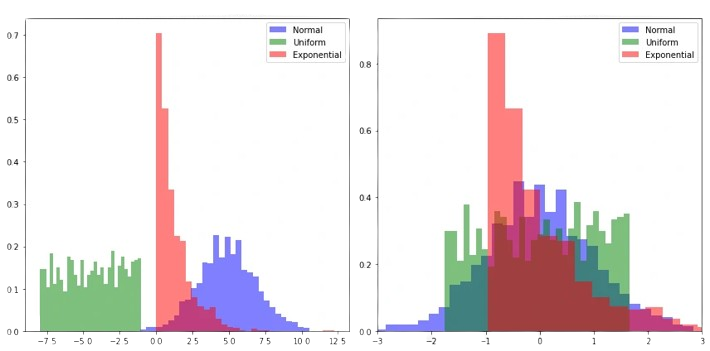
特征标准化是机器学习中的一个预处理步骤，其中输入特征被转换为平均值 0 和标准差 1。这通常是通过从每个特征的值中减去其平均值，然后除以标准差来实现的。

如果总体均值和总体标准差已知，则原始变量 x 将通过以下方式转换为标准分数

让我们尝试通过一个例子来理解这一点：
如果其中一个变量是公寓的价格（以数十万为单位），另一个变量是该公寓的房间数量（以单位为单位），则很难比较这两个数量。标准化后，它们的变量具有相似的值（尽管有点抽象），但它们的分布不会改变。

五、如何估计岭回归中的系数？

就像在回归的情况下，我们最小化了 RSS，对于岭回归，我们最小化了我们之前提到的表达式，但这次让我们用矩阵形式来表示它：

为了最小化 RSS_Ridge 表达式，我们将它的导数（相对于 β）设置为零。

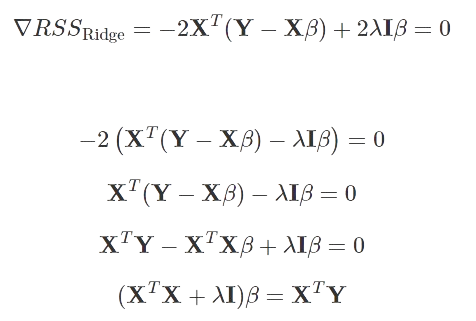
矩阵 X^TX+λI 具有满秩并且是可逆的。因此：

六、岭估计器的偏差-方差权衡

与最小二乘法相比，岭回归的优越性源于方差和偏差之间的固有权衡。岭回归引入了一个正则化参数，表示为 λ，该参数控制应用于回归系数的收缩程度。随着 λ 值的增加，模型拟合数据的灵活性会降低。因此，这种灵活性的降低导致方差同时减少，但偏倚增加。

我们注意到：

当预测变量数 p 接近观测值数 n 时，最小二乘法表现出高方差 — 训练数据的微小变化可能导致估计参数的显著变化。
当 p>n 时，最小二乘法停止工作（由于缺乏估计唯一性），而岭回归可以很好地处理这种情况。

6.1 例

假设我们有一个数据集，其中遗传标记（A， B， C， D， E）作为预测因子，性状（T）作为响应变量。

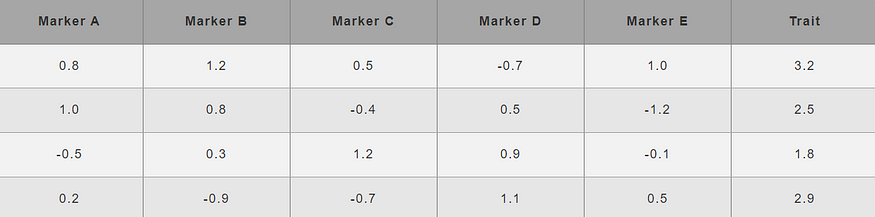
首先，我们需要为我们的方法指定超参数的值，即 λ.Let
λ=2。

从示例中获取数据，矩阵X_RAW采用以下形式：

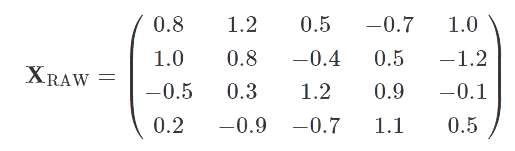
我们记得，在创建岭回归模型之前，我们需要对预测变量进行标准化，以便它们都具有 0 的平均值和 1 的标准差。对 z 分数使用一个简单的公式：

在标准化预测变量后，我们得到一个数据矩阵。

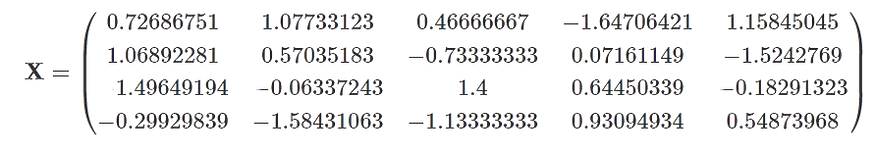
遗憾的是，标准化后，这些数字可能不便于计算。通常，计算机会为我们处理计算，但如果我们想逐步跟踪岭回归的工作原理，我们必须处理不方便的数字。

构建岭回归模型本质上意味着找到β系数（β我们理解系数向量（β1,...βp））。从我们之前的考虑中，我们已经知道获得它们的配方：

因此，首先，我们需要将转置矩阵 XT 乘以矩阵 X，然后将缩放的单位矩阵 I 与它相加，该矩阵由超参数 λ 缩放（在我们的例子中为 λ=2）。

请注意，结果取决于 λ 的值。如果我们改变 λ，我们会得到不同的结果。在下图中，我们可以观察到系数的估计值β如何根据所选参数 λ 而变化。

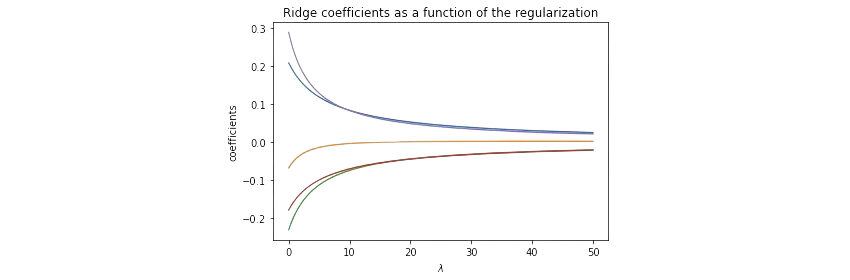
我们估计了系数 β1,...,βp，但是截距项 β0 呢？我们提到过，假设在进行岭回归之前，变量已居中为均值为零，则估计的截距将采用以下形式：

在我们的例子中：

现在，要计算预测，我们需要应用公式：

如果我们想使用模型预测目标变量的值，我们将获得以下值：

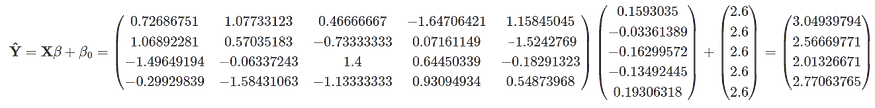
现在，我们可以将预测与实际值进行比较，以证明计算结果良好。

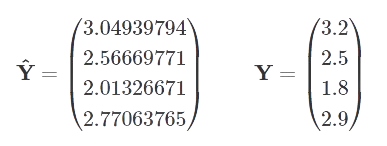
6.2 实现 — Ridge 回归

现在，我们将专注于实现我们的岭回归。我们将使用 Python 语言逐步完成。我们不会使用 class 来避免掩盖最重要的内容，即对算法工作原理的透彻理解。多亏了这一点，初学者将能够逐行执行代码并理解它。

首先，让我们生成一个数据集，与上一章中的示例完全相同。在此之前，我们还要导入必要的库。
我们还需要记住定义算法的超参数，即收缩参数 λ。就像在这个例子中一样，我们假设 λ=2。

import numpy as np
import pandas as pd
from numpy.linalg import inv

LAMBDA = 2

X = np.array([[0.8,  1.2,  0.5,  -0.7, 1.0],
              [1.0,  0.8,  -0.4, 0.5,  -1.2],
              [-0.5, 0.3,  1.2,  0.9,  -0.1],
              [0.2,  -0.9, -0.7, 1.1,  0.5]])

y = np.array([3.2, 2.5, 1.8, 2.9])

当然，我们必须记住，在创建岭回归模型之前，我们需要对预测因子进行标准化，以便它们都具有 0 的平均值和 1 的标准差。

X_scale = (X-X.mean(axis=0))/X.std(axis=0)

构建岭回归模型本质上意味着找到系数。从理论部分，我们学习了如何获得这些系数。使用公式就足够了：

为清楚起见，我们将本节分解为更小的步骤，以便可以跟踪矩阵上的每个操作。
函数 inv（）来自 numpy.linalg 模块。它计算矩阵的逆矩阵。同时，函数 np.identity（5）创建了一个大小为 5×5 的单位矩阵（因为我们有 5 个变量）。

# X*X^T + LAMBDA*I
x1 = np.matmul(X_scale.T, X_scale) + LAMBDA*np.identity(5)
# Transpose obtained matrix - (X*X^T + LAMBDA*I)^{-1}
x1_inv = inv(x1)
# ( (X*X^T + LAMBDA*I)^{-1} ) * X^T
x2 = np.matmul(x1_inv, X_scale.T)
# ( ( (X*X^T + LAMBDA*I)^{-1} ) * X^T ) * Y
coef = np.matmul(x2, y)
# Estimated coeficients
print(coef)

我们得到了以下系数，与上一节中的示例完全相同。

[3.04939794, 2.56669771, 2.01326671, 2.77063765]

要计算预测，我们需要应用公式

从前面的考虑中，我们记得 β0 只是目标变量的平均值。

np.matmul(X_scale, coef)+y.mean()

最后，这里又是整个代码：

import numpy as np
import pandas as pd
from numpy.linalg import inv

LAMBDA = 2    # shrinkage parameter

# Define dataset (X,y)
X = np.array([[0.8,  1.2,  0.5,  -0.7, 1.0],
              [1.0,  0.8,  -0.4, 0.5,  -1.2],
              [-0.5, 0.3,  1.2,  0.9,  -0.1],
              [0.2,  -0.9, -0.7, 1.1,  0.5]])

y = np.array([3.2, 2.5, 1.8, 2.9])

# Scale predictors
X_scale = (X-X.mean(axis=0))/X.std(axis=0)

# RIDGE REGRESSION MODEL - coefficients estimation
# X*X^T + LAMBDA*I
x1 = np.matmul(X_scale.T, X_scale) + LAMBDA*np.identity(5)
# Transpose obtained matrix - (X*X^T + LAMBDA*I)^{-1}
x1_inv = inv(x1)
# ( (X*X^T + LAMBDA*I)^{-1} ) * X^T
x2 = np.matmul(x1_inv, X_scale.T)
# ( ( (X*X^T + LAMBDA*I)^{-1} ) * X^T ) * Y
coef = np.matmul(x2, y)
# Estimated coeficients
print(coef)

# predictions
np.matmul(X_scale, coef)+y.mean()