反电诈题材影片《孤注一掷》取材于真实案例,揭秘了境外电信网络诈骗黑色产业链的骇人内幕。境外诈骗集团往往以高薪招聘为诱饵,吸引有发财梦的人去境外淘金,一旦人们走出国门,跳入犯罪分子设下的陷阱里,等待他们的将是拘禁、威胁、殴打和洗脑,在无尽的恐惧和残忍的折磨下,他们的意志力消磨殆尽,渐渐沦为诈骗集团的工具和帮凶,设套引诱更多的人加入诈骗团伙、壮大自身力量或者在境外通过电信网络实施诈骗。

电影开篇,女警官介绍了赌博里面的数学逻辑,其中博弈论是赌博机制的核心数学逻辑。

博弈论,又称为对策论(Game Theory)、赛局理论等,是现代数学的一个新分支,也是运筹学的一个重要学科。它主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。

一、发展历程
博弈论的思想古已有之,中国古代的《孙子兵法》等著作就不仅是一部军事著作,而且算是最早的一部博弈论著作。博弈论最初主要研究象棋、桥牌、赌博中的胜负问题,人们对博弈局势的把握只停留在经验上,没有向理论化发展。近代对于博弈论的研究,开始于策梅洛(Zermelo)、波 莱尔(Borel)及冯·诺依曼(von Neumann)。1928年,冯·诺依曼证明了博弈论的基本原理,从而宣告了博弈论的正式诞生。1944年,冯·诺依曼和摩根斯坦共著的划时代巨著《博弈论与经济行为》将二人博弈推广到n人博弈结构并将博弈论系统地应用于经济 领域,从而奠定了这一学科的基础和理论体系。1950年~1951年,约翰·福布斯·纳什(John Forbes Nash Jr)利用不动点定理证明了均衡点的存在,为博弈论的一般化奠定了坚实的基础。纳什的开创性论文《n人博弈的均衡点》(1950),《非合作博弈》(1951)等等,给出了纳什均衡的概念和均衡存在定理。此外,莱因哈德·泽尔腾、约翰·海萨尼的研究也对博弈 论发展起到推动作用。

二、应用范围
博弈论在经济学、金融学、证券学、生物学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。例如,在经济学中,博弈论已经成为标准分析工具之一,被用来分析经济和贸易竞争。在国际政治领域,博弈论模型也被广泛用来分析国家间安全问题和经济问题,如“懦夫游戏”(chicken game)、“囚徒困境”、“针对不平等的威胁对策”和“协调对弈”等。

三、主要类型
博弈论有两种基本的类型,即“同时博弈”和“序贯博弈”。前者是参与人同时进行决策或行动的博弈,后者是参与人的决策和行动有先有后的博弈。此外,博弈论还有多种分类方式,如根据信息是否完全,可以分为完全信息博弈和不完全信息博弈;根据博弈的重复次数,可以分为单次博弈和重复博弈等。

四、核心要素
局中人:在一场竞赛或博弈中,每一个有决策权的参与者成为一个局中人。只有两个局中人的博弈现象称为“两人博弈”,而多于两个局中人的博弈称为“多人博弈”。
策略:一局博弈中,每个局中人都有选择实际可行的完整的行动方案,即方案不是某阶段的行动方案,而是指导整个行动的一个方案。一个局中人的一个可行的自始至终全局筹划的一个行动方案,称为这个局中人的一个策略。
得失:一局博弈结局时的结果称为得失。每个局中人在一局博弈结束时的得失,不仅与该局中人自身所选择的策略有关,而且与全局中人所取定的一组策略有关。所以,一局博弈结束时每个局中人的“得失”是全体局中人所取定的一组策略的函数,通常称为支付(payoff)函数。

五、重要概念
纳什均衡:它是一稳定的博弈结果。在博弈论中,如果每个局中人都预测到,无论其他局中人如何选择策略,自己选择的策略都是最优的,那么这个策略组合就被称为纳什均衡。

六、影响与荣誉
从1994年诺贝尔经济学奖授予3位博弈论专家开始,共有7届的诺贝尔经济学奖与博弈论的研究有关。这些获奖者的研究不仅推动了博弈论的发展,也对经济学、政治学、社会学等多个领域产生了深远影响。

博弈论作为一门研究具有斗争或竞争性质现象的数学理论和方法,在现代科学和社会发展中具有广泛的应用和重要的学术价值。
【观影聊数学】聊聊电影《孤注一掷》中的数学逻辑
news2026/2/11 10:04:07
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2137368.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
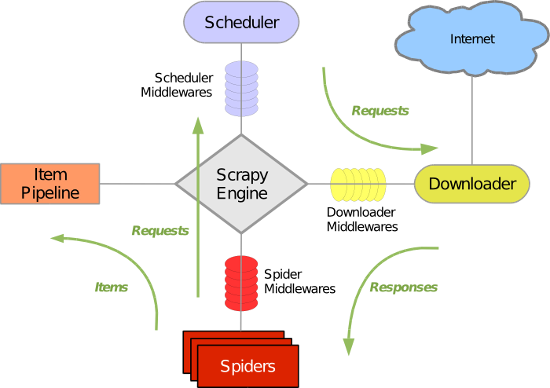
【python爬虫】之scrapy框架介绍
一.什么是Scrapy? Scrapy是一个为了爬取网站数据,提取结构性数据而编写的应用框架,非常出名,非常强悍。所谓的框架就是一个已经被集成了各种功能(高性能异步下载,队列,分布式,解析&a…
SpringBoot开发——使用@Slf4j注解实现日志输出
文章目录 1、Lombok简介2、SLF4J简介3、实现步骤3.1 创建SpringBoot项目3.2 添加依赖3.3 使用 Slf4j 注解3.4 输出日志信息 4、结论 在现代Java开发中,日志记录是至关重要的。它不仅帮助开发者调试代码,还便于监控系统运行状态和性能。 Lombok 和 SLF4J …
了解水凝胶纤维制造?自润滑纺丝来帮忙!高韧性纤维用途广!
大家好,今天我们来了解一篇水凝胶纤维文章——《Continuous Spinning of High‐Tough Hydrogel Fibers for Flexible Electronics by Using Regional Heterogeneous Polymerization》发表于《Advanced Science》。在柔性电子领域,水凝胶纤维因其独特的性…
检查一个复数C的实部a和虚部b是否都是有限数值即a和b都不是无限数值、空值cmath.isfinite(x)
【小白从小学Python、C、Java】 【考研初试复试毕业设计】 【Python基础AI数据分析】 检查一个复数C的实部a和虚部b 是否都是有限数值 即a和b都不是无限数值、空值 cmath.isfinite(x)
[太阳]选择题
根据给定的Python代码,哪个选项是错误的? import cma…
适合小客厅使用的投影仪推荐:2024年当贝X5S小户型客厅的最佳选择
我们在买投影前都会先看看家里的环境、预算以及自己的需求去选择适合自己的家的那款;正好最近有朋友向我资讯:我家客厅面积不大,有没有适合的家用投影仪推荐啊?对于这种家庭使用环境不大的小客厅我们该如何挑选投影仪?…
人员抽烟AI检测算法在智慧安防领域的创新应用,助力监控智能化
随着人工智能技术的飞速发展,计算机视觉和深度学习算法在各个领域的应用日益广泛。其中,人员抽烟AI检测算法以其高效、精准的特点,成为公共场所、工厂、学校等场景中的得力助手。本文将介绍TSINGSEE青犀AI智能分析网关V4人员抽烟检测算法的基…
JavaScript高级——执行上下文栈
1、在全局代码执行前,JS引擎就会创建一个栈来存储管理所有的执行上下文对象
2、在全局执行上下文(window)确定后,将其添加到栈中(压栈)
3、在函数执行上下文创建后,将其添加到栈中(…
AI 驱动腾讯游戏智能 NPC,开启新纪元
AI 驱动腾讯游戏智能 NPC,开启新纪元 前言AI 驱动腾讯智能 NPC 前言 曾经,游戏 NPC 往往只是按照预设脚本进行简单互动,缺乏深度和灵活性。然而,如今在 AI 的赋能下,NPC 开始展现出前所未有的智能与活力。它们能够进行…
【springboot】父子工程项目搭建
父工程创建
1.新建一个spring项目 2.选择合适的springboot版本,点击【完成】,即创建父工程完毕
3.删除父工程中无用文件:src 创建子工程模块
1.右键项目名->新建(news)->模块(Module)…
【数据结构与算法】巧用位运算
【数据结构与算法】巧用位运算 文章目录 【数据结构与算法】巧用位运算位运算的巧思用位运算来求集合公式用位移求集合公式二进制库函数 位扩展:基础例题例题LC190——用到左移和或运算异或运算法则经典例题:[LC136 唯一数](https://leetcode.cn/problem…
stm32单片机个人学习笔记3(GPIO输出)
前言
本篇文章属于stm32单片机(以下简称单片机)的学习笔记,来源于B站教学视频。下面是这位up主的视频链接。本文为个人学习笔记,只能做参考,细节方面建议观看视频,肯定受益匪浅。
STM32入门教程-2023版 细…
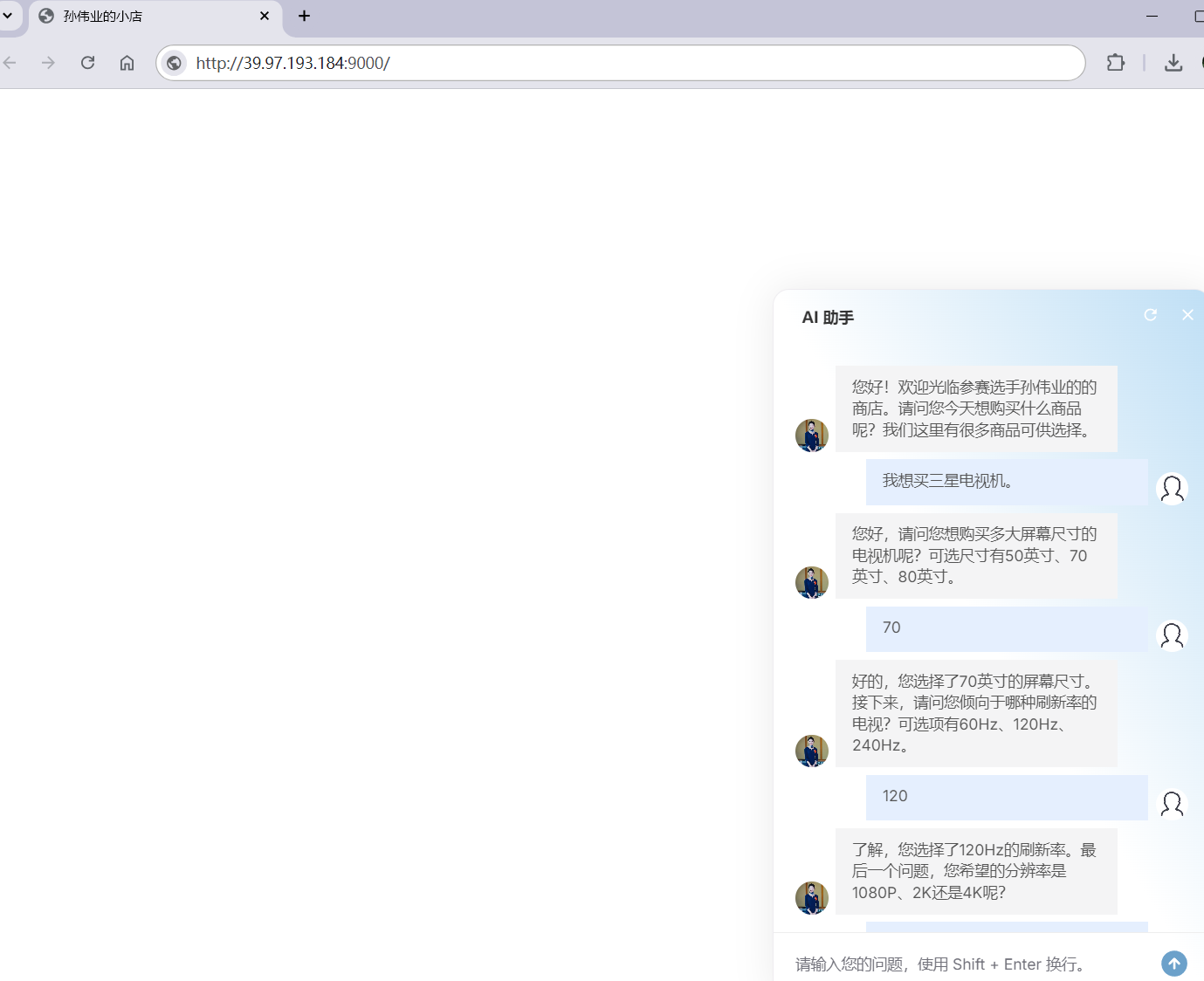
基于千问大模型Intel G8i开发主动问询导购助手
文章目录 1. 背景2.环境介绍2.1 硬件环境2.2 软件环境 3. 大模型环境部署3.1 准备硬件资源 3.2 大模型部署3.1 部署Docker3.2 部署Intel xFasterTransformer容器3.3 准备模型数据3.4 运行模型进行AI对话 4. 构建主动问询导购助手应用 1. 背景
北京又开始发放消费券啦ÿ…
整个场面要hold住-《分析模式》漫谈32
DDD领域驱动设计批评文集
做强化自测题获得“软件方法建模师”称号
《软件方法》各章合集 “Analysis Patterns”的第一章有这么一句:
It is important to be clear to them that I am not holding them up as gospel, and if they are not comfortable, I will …
RedisTemplate操作ZSet的API
文章目录 ⛄概述⛄常见命令有⛄RedisTemplate API❄️❄️ 向集合中插入元素,并设置分数❄️❄️向集合中插入多个元素,并设置分数❄️❄️按照排名先后(从小到大)打印指定区间内的元素, -1为打印全部❄️❄️获得指定元素的分数❄️❄️返回集合内的成员个数❄️❄…
鸿蒙应用开发:音频播放
鸿蒙系统提供了多样化的API,来帮助开发者完成音频播放的开发,不同的API适用于不同音频数据格式、音频资源来源、音频使用场景,甚至是不同开发语言。因此,选择合适的音频播放API,有助于降低开发工作量,实现更佳的音频播放效果。
本节介绍通过Media Kit实现音频播放。 AVP…
【机器学习】--- 深度学习中的注意力机制
深度学习中的注意力机制
在深度学习领域,注意力机制(Attention Mechanism)已经成为近年来最受瞩目的研究热点之一。它不仅提升了现有模型的性能,更启发了全新的网络结构,如Transformer模型。注意力机制被广泛应用于自…
SMA2:代码实现详解——Image Encoder篇(Hiera章)
SMA2:代码实现详解——Image Encoder篇(Hiera)
写在前面
大家在SMA2:代码实现详解——Image Encoder篇(FpnNeck)下的留言我已收到,感谢大家的支持,后面如果遇到比较难以讲清的部分可能会使用视频的形式。…
jsp+sevlet+mysql图书管理系统
jspsevletmysql图书管理系统 一、系统介绍二、功能展示1.图书查询(学生)2.借阅信息(学生)3.借阅历史(学生)4.借阅历史(管理员)5.读者管理(管理员)6.图书分类(管理员)7.图书借阅信息(管理员)8.图书归还信息(管理员) 四、其它1.其他系统实现 一、系统介绍
系统主要功能ÿ…
《Linux运维总结:基于ARM64+X86_64架构CPU使用docker-compose一键离线部署mongodb 7.0.14容器版副本集群》
总结:整理不易,如果对你有帮助,可否点赞关注一下?
更多详细内容请参考:《Linux运维篇:Linux系统运维指南》 一、部署背景 由于业务系统的特殊性,我们需要面向不通的客户安装我们的业务系统&…