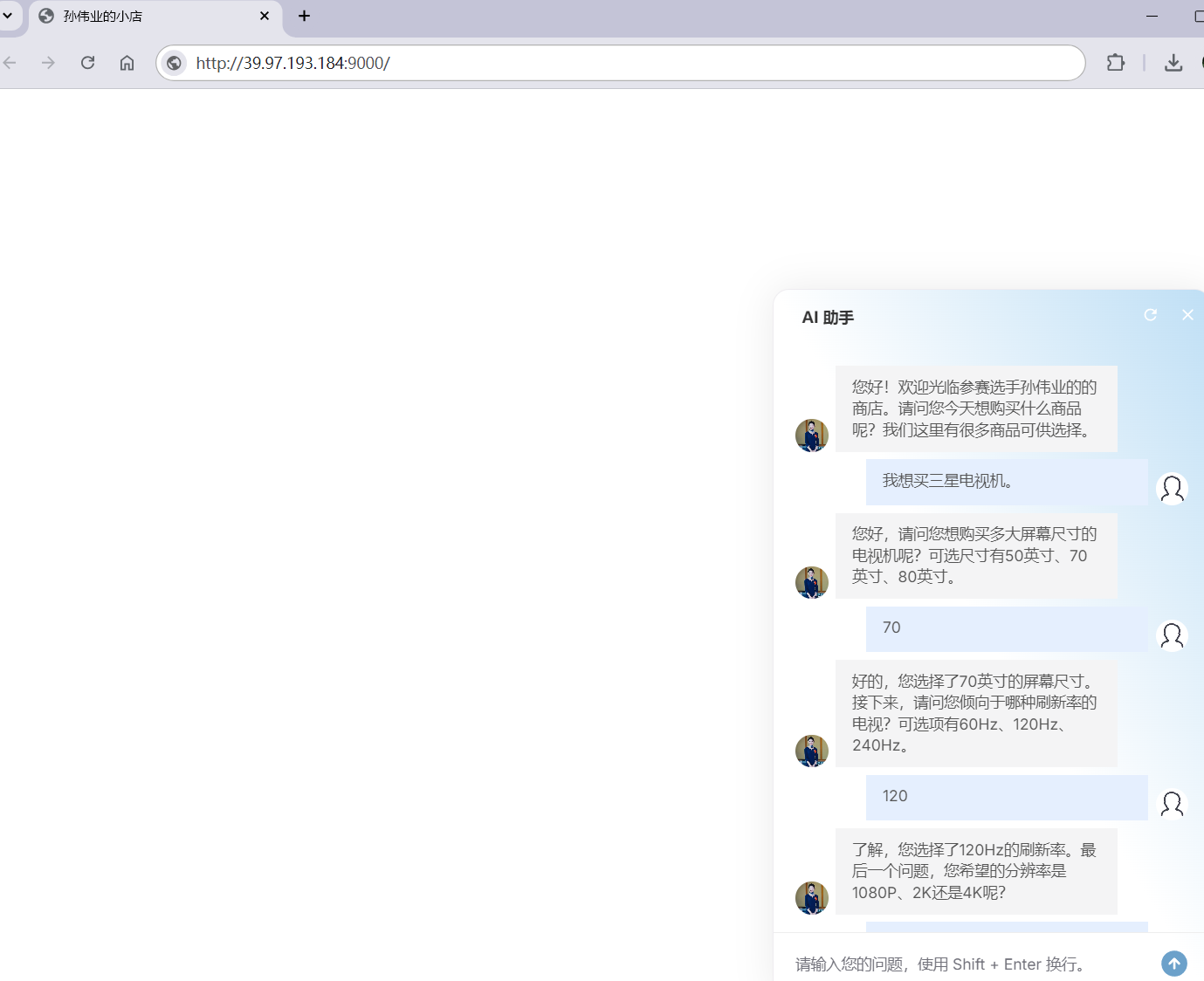
【数据结构与算法】巧用位运算
文章目录
- 【数据结构与算法】巧用位运算
- 位运算的巧思
- 用位运算来求集合公式
- 用位移求集合公式
- 二进制库函数
- 位扩展:基础例题
- 例题LC190——用到左移和或运算
- 异或
- 运算法则
- 经典例题:[LC136 唯一数](https://leetcode.cn/problems/single-number/description/)
位运算的巧思
总结来源:分享|从集合论到位运算,常见位运算技巧分类总结!
用位运算来求集合公式
术语:
- 与:
&11为1 ,其余为0 - 或:
|有1为1, 00为0 - 异或:
⊕(^)相异为1, 相同为0 - 反:
~按位取反
| 术语 | 集合 | 位运算 | 集合示例 | 位运算示例 |
|---|---|---|---|---|
| 交集 | A∩B | a&b | {0,2,3} ∩{0,1,2} ={0,2} | 1101 &0111 = 0101 |
| 并集 | A∪B | a|b | {0,2,3} ∪{0,1,2} ={0,2} | 1101 | 0111 = 1111 |
| 对称差 A,B相交以外的元素 | AΔB | a^b | {0,2,3} Δ{0,1,2} ={1,3} | 1101 ^0111 =1010 |
| 差(B不为子集) | A\B | a&(~b) | {0,2,3} \{1,2} ={0,3} | 1101 &1001 =1001 |
| 差(B为子集) | A\B B⊆A | a^b | {0,2,3} \{0,2} ={3} | 1101 ^0101 =1000 |
| 包含于 | A⊆B | a&b == a or(用于判断) a|b == b | {0, 2} ⊆{0,2,3} | 0101&1101==0101 OR 0101 | 1101 == 0101 |
用位移求集合公式
术语:
- 左移
<<:低位补零,相当于乘以 2 i 2^i 2i - 右移
>>: 高位补零,相当于除以 2 i 2^i 2i
补充说明,在使用集合和位运算的过程中,我们需要明确,它们是如何一一对应的。
假设我们有一个不包含相同元素的数组,大小为32。
- 如果全部元素都已经选中,则其表示的集合当为全集——
(1 << 32) -1因为这样我们会得到32个1,1代表该index的元素已被选中。
现在我们根据某规则从其中已经挑选一些元素,现在仍需继续挑选一些元素,假设已挑选的集合为s
我们判断index 为 i的元素是否被选中,可以使用
(s >> i) & 1 == 1进行判断,其原理是把i位的元素右移到末尾,相与计算是否被选中。其余计算巧思见下图
| 术语 | 集合 | 位运算 | 集合示例 | 位运算示例 |
|---|---|---|---|---|
| 空集 | 0 | |||
| 单元素集合 | {i} | 1 << i | {2} | 1 << 2 |
| 全集 | U={0,1,2,⋯n−1} | (1 << n)−1 | {0,1,2,3} | (1 << 4)−1 |
| 补集 | ∁u𝑆=𝑈∖𝑆 | ((1 << n)−1)⊕s | U={0,1,2,3} S = {1,2} S相对于U的补集 是U中所有不属于S中的元素 这里的U为全集,故S包含于U | 1111 ^ 0110 =1001 |
| 属于 | i ∈ S | (s>>i)&1 == 1 | 2 ∈ {0,2,3} | (1101 >> 2)& 1 ==1 |
| 不属于 | i∈/S | (s >> i) & 1 ==0 | 1∈/{0,2,3} | (1101 >> 1) & 1== 0 |
| 添加元素 | S U {i} | s | (1 << i) | {0,3}∪{2} | 1001 ∣ (1 << 2) |
| 删除元素 | S∖{i} | s&∼(1 << i) | {0,2,3}∖{2} | 1101&∼(1 << 2) |
| 删除元素 (删除的是子集) | S∖{i}, i∈S | s⊕(1 << i) | {0,2,3}∖{2} | 1101 ^(1 << 2) |
| 删除最小元素 (删除最低位元素) | s & (s - 1) | 备注:如果s为2的幂次方, 那么结果为0 | s = 101100 s-1 = 101011 s&(s-1) = 101000 | |
| 包含最小元素的子集(lowbit) | 即二进制最低1 及之后的0 | s & (-s) | (-s)这是补码,不是位反, 及最低1左侧取反,右侧不变 | s = 101100 ~s = 010011 -s = (~s)+1 = 010100 s & -s = 000100 |
二进制库函数
注意,当s = 0时,对以下API可能属于未定义行为
对C++ 的
long long,需使用__builtin_popcountll,即函数名后添加ll(小写L)
| 术语 | C++ | 说明 |
|---|---|---|
| 集合大小 | __builtin_popcount(s) | 计算s的二进制表达中1的个数 |
| 二进制长度 | 32-__builtin_clz(s) | __builtin_clz()返回从最高位开始的前导0的个数 |
| 集合最大元素 | 31-__builtin_clz(s) | |
| 集合最小元素 | 31-__builtin_clz(s) |
位扩展:基础例题
- LeetCode 78 组合:
不含重复值的整数数组的所有子集 - 核心代码:
def subsets(self, nums):
'''
位扩展写法:把新的元素依次加到前面的结果集里
组成新的集合再加入结果集
注意:不要超过本轮的结果集
'''
res = [[]]
for value in nums:
long = len(res)
for pos in range(long):
temp = copy.deepcopy(res[pos])
temp.append(value)
res.append(temp)
return res
例题LC190——用到左移和或运算
示例代码1:
uint32_t reverseBits(uint32_t n)
{
uint32_t rev = 0;
for (int i = 0; i < 32 && n > 0; ++i)
{
// n&1使用的是n的末尾与1相与,末位为1则为1
// |= 有1为1,全0为0
// 这里相当于,不断把n的低位数传到rev未定义的高位
rev |= (n & 1) << (31 - i);
/*
如:
n = 00000010100101000001111010011100
i = 0
n&1 = 0
31-i = 31
(n&1)<<(31-i)得到的是
0(这是当前匹配的结果0)【因为是左移,后面补31个0】
形象点就是把n的末尾直接传送到了rev的最高位。
也就是这个循环的意义。
*/
// 去掉已经传递的末尾
n >>= 1;
}
return rev;
}
异或
基本概念:如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。
运算法则

在C++中用^符号表示异或,可以用异或交换两个数
void swap(int &a, int &b){
a = a^b;
b = b^a; //b = b^a^b = a
a = a^b; // a = a^b^a = b
}