Minitab 的直方图结果分析解释

步骤 1：评估关键特征

检查分布的尖峰和散布。评估样本数量对直方图外观的影响。

标识尖峰（即，条的最高聚类）：

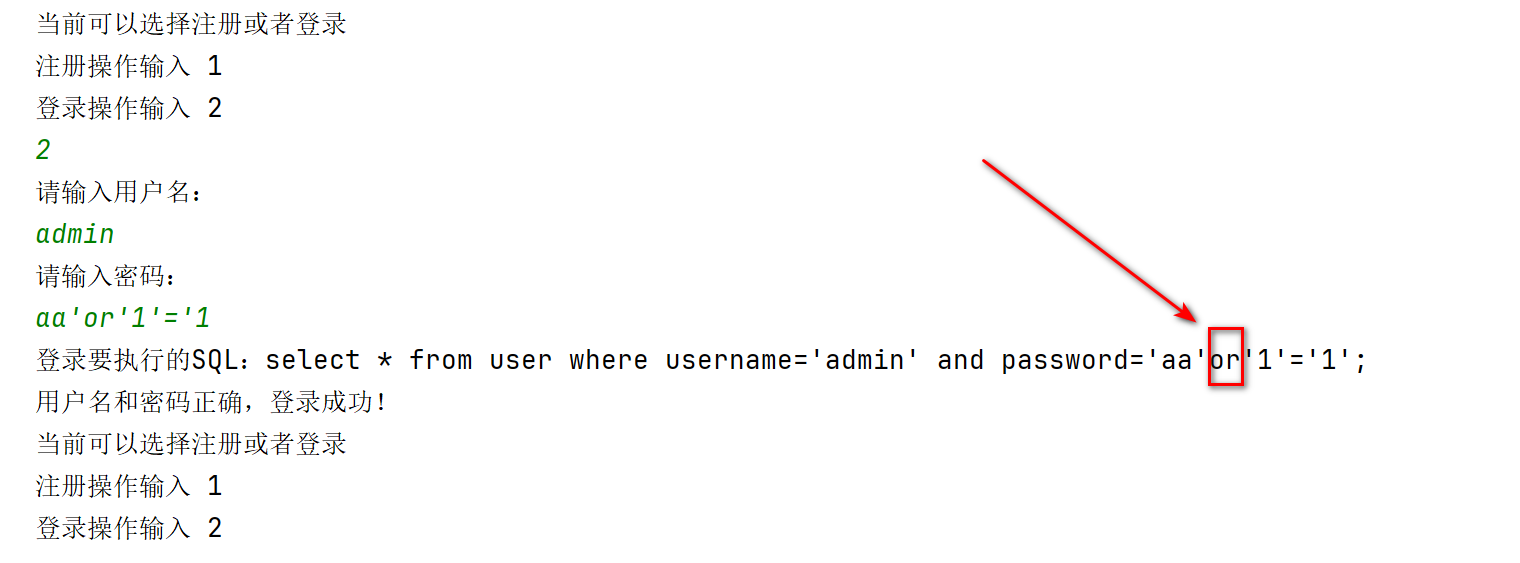
尖峰表示样本中最常见的值。评估样本的散布以了解数据的变异程度。例如，在客户等待时间的此直方图中，数据的尖峰出现在大约 6 分钟处。数据大约散布在 2 分钟到 12 分钟之间。

观察此直方图上任何奇怪的或不需要的特征。例如，客户等待时间的直方图显示的散布宽度超出预期。经观察发现，是计算机软件更新导致了客户等待时间延迟。

样本数量 (n)：样本数量可能会影响图形的外观。

例如，尽管这两个直方图似乎有相当大的差异，但它们都是使用从同一个总体中随机选择的数据样本创建的。

当样本数量最少为 20 时，直方图效果最佳。如果样本数量太小，直方图上每个条形包含的数据点不足，无法准确显示数据的分布情况。样本越大，直方图与总体分布的形状越相似。如果样本数量小于 20，请考虑改用单值图。

步骤 2：查找非正常或异常数据的指示符

偏斜数据和多模态数据表明数据可能不正常。异常值可能表明数据中存在其他情况。

偏斜数据：当数据偏斜时，大多数数据位于图形的高或低侧。偏斜表明数据可能未呈正态分布。

这些直方图说明的是偏斜数据。带右偏斜数据的直方图显示等待时间。大部分等待时间相对较短，只有少数等待时间很长。带左偏斜数据的直方图显示失效时间数据。少数几个项立即失败，更多的项会在随后失败。

如果已知数据本身未偏斜，请观察可能的原因。如果希望分析严重偏斜的数据，请分析“数据注意事项”主题，以确保可以使用非正常数据。

异常值：异常值是远离其他数据值的数据值，可能会显著影响的结果。通常情况下，在箱线图上最容易识别异常值

在直方图上，两端上的孤立条形标识异常值。尝试确定导致任何异常值的原因，更正任何数据输入错误或测量误差。考虑删除与异常的单次事件（也称为特殊原因）相关联的数据值。然后，重新执行分析。

多模态数据：多模态数据具有多个峰值。（峰值表示一组数据的模式。）如果数据是从多个过程中或在多个条件（如多个温度）下收集的，通常会出现多模态数据。

例如，这些直方图是包含相同数据的图形。简单直方图包含两个尖峰，但它并未清楚地指示尖峰的含义。含组的直方图表明，尖峰与两个组相对应。

如果具有其他可用来对观测值进行分组的信息，则可以创建一个包含此信息的组变量。然后，可以创建含组的图形，以确定组变量是否导致数据中的峰值。

步骤 3：评估对分布的拟合

如果直方图含拟合分布线，请评估条形的高度对分布线形状的服从紧密程度。如果下面的条形紧密地服从拟合分布线，则数据能够很好地拟合分布。

步骤 4：评估和比较组

如果直方图含组，请评估和比较组的中心和散布。

中心：查找组中心之间的差异。

例如，这些直方图显示三个版本的信用卡应用程序的完成时间。每个版本的信用卡应用程序的中心位于一个不同的位置。位置差异表明完成时间的均值存在差异。

要确定均值的差值在统计意义上是否显著，可以进行如下操作：

    如果只有两个组，请使用双样本 t 检验。

    如果有三个或多个组，请使用单因子方差分析。

散布：查找组散布之间的差异。

例如，这些直方图显示由三台机器填充的罐子的重量。尽管这些直方图的中心几乎相同，但有些直方图比较宽和分散。散布得越宽，这些机器对罐子的填充越不一致。

要确定散布（方差）之间的差异在统计意义上是否显著，可以进行如下操作：
如果只有两个组，请使用双方差检验。
如果有三个或多个组，请使用等方差检验。